Одной из важных проблем в области системного анализа является исследование динамики функционирования сложных технических, производственных и экономических систем на различных этапах их проектирования, испытания и эксплуатации, а также управление этими системами на основе результатов проведенного исследования. При проведении математического моделирования сложной системы многие задачи связаны с выбором вариантов результатов экспериментальных расчетов, на основе которых в дальнейшем формируются управляющие воздействия с целью корректировки процесса функционирования системы. В их числе задачи определения допустимых или наилучших параметров управления этой системой в дискретные моменты времени с целью обеспечения заданных критериев (эффективности, надежности и других показателей) качества ее функционирования. Зачастую необходимость выбора значений таких параметров возникает в процессе управления в нестандартных ситуациях, а также при постановке и решении оптимизационных задач. Разработка средств поддержки многокритериального выбора для предметного специалиста является актуальной проблемой в области ситуационного управления [3].
Важными характеристиками механизма выбора для лица, принимающего решение – специалиста предметной области, являются простота в использовании и скорость выполнения вычислений, необходимых для выработки управляющих воздействий. Простота использования механизма выбора обуславливает в свою очередь требование минимального объема входной информации, предоставляемой специалистом предметной области и необходимой для работы этого механизма.
В статье рассматривается подход к управлению сложной системы на основе методологии многокритериального выбора значений наблюдаемых переменных, получаемых в процессе имитационного моделирования этой системы. В рамках данного подхода разработан специализированный алгоритм, базирующийся на использовании известных методов многокритериального выбора и обеспечивающий вышеперечисленные характеристики механизма выбора управляющих воздействий. Сложная система рассматривается как система массового обслуживания.
Постановка задачи
Предполагается, что в процессе управления сложной системой S специалисту предметной области необходимо произвести исследование системы с помощью имитационного моделирования и определить управляющие воздействия на систему с целью повышения эффективности ее функционирования.
Модель многокритериального выбора. Пусть x и y – векторы входных и наблюдаемых переменных имитационной модели исследуемой системы S. Наблюдаемые переменные представляют показатели качества функционирования исследуемой системы. Элементы векторов xi,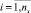 
, и yj, 
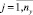имеют соответственно области Xi и Yj допустимых значений. Предполагается, что эффекты влияния входных переменных на наблюдаемые переменные исследованы с помощью факторного анализа [4] заранее – при построении и испытании имитационной модели исследуемой системы. Также предполагается, что для каждого j-го элемента вектора y задан критерий вычисления оценки 
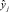качества значения этого элемента (стремление значения к минимуму или максимуму на множестве сравниваемых значений) и его предельные значения 
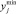и 
.
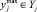Ряд элементов вектора x играют роль варьируемых переменных, образуют подмножество X* и отождествляются с элементами вектора u управляющих воздействий: uq ≡ xi,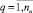 
, 
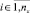, 1 ≤ nu ≤ nx. В качестве начальных значений варьируемых переменных используются базовые значения, соответствующие принятым по параметрам функционирования исследуемой системы. Остальные значения варьируемых переменных выбираются из соответствующих областей допустимых значений с учетом эффектов влияния варьируемых переменных на наблюдаемые переменные. Значения неварьируемых входных переменных, являющихся элементами вектора x, задаются на основе статистических числовых данных, представленных информационной подсистемой исследуемой системы.
Специалистом предметной области инициируется процесс имитационного моделирования с некоторым периодом дискретности T. В процессе моделирования выполняется имитация процесса функционирования исследуемой системы путем проведения параллельных многовариантных расчетов (прогона модели для каждого сочетания значений варьируемых переменных) и формируется множество V вариантов значений наблюдаемых переменных: значение yjk ∈ Yj является элементом k-го варианта vk ∈ V для переменной yj,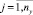 
, 
.
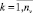Таким образом, модель многокритериального выбора можно представить в виде структуры: M = <x, y, u, X*, V, Y*, С>, где Y* – множество оценок значений наблюдаемых переменных из V, С – механизм многокритериального выбора.
Постановка задачи многокритериального выбора. Пусть выполнено имитационное моделирование исследуемой системы S и сформировано множество V вариантов значений наблюдаемых переменных модели M. По результатам имитационного моделирования на модели M требуется с помощью механизма C сформировать вектор u управляющих воздействий путем многокритериального выбора варианта vk значений наблюдаемых переменных из V и варьируемых переменных из X*, отождествляемых с элементами вектора u и соответствующих значениям наблюдаемых переменных выбранного варианта vk. Механизмы многокритериального выбора на основе лексикографического и мажоритарного методов рассматриваются в следующем разделе.
Методология многокритериального выбора
Выбор из множества V подмножества V* ⊆ V вариантов значений наблюдаемых переменных с целью дальнейшего определения значений элементов вектора u является многокритериальным. Существует широкий спектр методов принятия решений на основе многокритериальной оптимизации [7]. Из этого спектра для решения поставленной задачи наиболее подходят некоторые распространенные методы многокритериального выбора, основанные на анализе числовых значений в соответствии с заданными критериями качества и оценками этих значений. В их числе методы выбора по Парето и по взвешенному критерию, совокупно-экстремальный, лексикографический и мажоритарный методы [5]. Применение ряда методов, таких как метод выбора по взвешенному критерию, требует от специалиста предметной области больших трудозатрат при определении рангов, весов и других характеристик критериев, что на практике бывает крайне затруднительно. В случае методов, подобных совокупно-экстремальному методу, возникает проблема интерпретации результатов выбора. При использовании метода выбора по Парето задача выбора зачастую может быть неразрешимой.
Таким образом, в рамках данного исследования выбор вариантов для подмножества V* осуществляется либо на основе лексикографического метода, если специалист предметной области может упорядочить наблюдаемые переменные по значимости, либо, в противном случае, на основе мажоритарного метода. Лексикографический метод отбора вариантов значений наблюдаемых переменных использует следующее правило многокритериального выбора, приведенное в [5]:
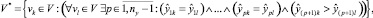(1)
где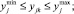 
, 
, 
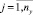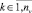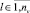, k ≠ l.
Мажоритарный метод отбора вариантов значений наблюдаемых переменных использует следующее правило многокритериального выбора, приведенное в [5]:
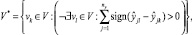(2)
где sign(0) = 0;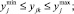 
, 
, 
.
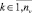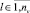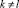Для оценки значений yjk,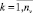 
j-й переменной их множество разбивается на подмножества, попарно непересекающиеся, которые упорядочиваются по возрастанию или убыванию значений наблюдаемых переменных, содержащихся в них. В соответствии с этим упорядочением каждое подмножество получает свой индекс, который используется в качестве оценки значений наблюдаемых переменных, попавших в данное подмножество. Оценка значений yjk, 
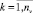для каждой j-й переменной может выполняться параллельно.
Применение рассмотренных выше методов многокритериального выбора обусловлено тем, что они обладают наименьшей сложностью с вычислительной точки зрения по сравнению с другими известными методами решения подобной задачи, просты в реализации и требуют минимальную дополнительную информацию от эксперта.
Пусть в результате формирования множества V* получен единственный k-й вариант vk значений наблюдаемых переменных. Этому вектору однозначно соответствует k-й вариант значений варьируемых переменных вектора x. Выбрав из них значения xik такие, что xi ∈ X*, получим значения элементов вектора u. В том случае, когда полученное подмножество V* содержит более одного варианта значений наблюдаемых переменных, окончательный выбор единственного варианта vl осуществляется случайным образом. При V* = ∅ задача неразрешима. В этом случае требуется вмешательство лица, принимающего решение, с целью корректировки исходных данных.
Алгоритм многокритериального выбора управляющих воздействий
Работа алгоритма многокритериального выбора значений наблюдаемых переменных, входящих в модель исследуемой системы, включает четыре фазы.
I. Фаза подготовки исходных данных
а) Проведение факторного анализа имитационной модели исследуемой системы. Построение векторов x, y и u. Определение степени влияния варьируемых переменных на наблюдаемые переменные.
b) Определение метода многокритериального выбора и задание критериев вычисления оценок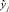 
качества значений элементов вектора y и их предельных значени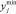й 
и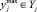 
, 
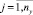. В случае лексикографического метода – упорядочение наблюдаемых переменных.
c) Задание значений исходных данных.
II. Фаза имитационного моделирования
а) Автоматическое формирование множества вариантов исходных данных на основе значений варьируемых переменных.
b) Имитация процесса функционирования исследуемой системы путем проведения параллельных многовариантных расчетов и формирование множества V вариантов значений наблюдаемых переменных.
III. Фаза анализа результатов моделирования
а) Определение оценок значений наблюдаемых переменных.
b) Решение задачи многокритериального выбора значений наблюдаемых переменных.
IV. Фаза принятия решения
а) Если задача неразрешима, то переход на один из шагов фазы I) с целью корректировки исходных данных или переход на шаг с. текущей фазы.
b) Если задача разрешима, то формирование вектора u.
c) Завершение работы алгоритма.
Операции на фазе подготовки исходных данных осуществляются специалистами предметной области: шаг (a) – разработчиком модели; шаги (b) и (c) – конечным пользователем модели. Принятие решения на шаге (a) четвертой фазы работы алгоритма также осуществляется конечным пользователем модели. Алгоритм определения оценок значений наблюдаемых переменных хорошо распараллеливается и масштабируется. При распараллеливании вычислений на ny процессов сложность определения оценок значений наблюдаемых переменных в худшем случае можно оценить как O(nvlognv). При решении задачи многокритериального выбора лексикографическим или мажоритарным методами сложность не превышает O(nynv).
Вычислительные эксперименты
Данный алгоритм использован в инструментальных средствах автоматизации проведения вычислительных экспериментов по имитационному моделированию сложных систем [1]. Для иллюстрации работы алгоритма в табл. 1 и 2 приведены выборочные результаты вычислений.
В табл. 1 приведены результаты эксперимента для задачи моделирования складского комплекса [2]. Варианты v4 и v5 отбрасываются, так как значения ряда наблюдаемых переменных в данных вариантах выходят за пределы областей допустимых значений этих переменных. Значения, выходящие за пределы допустимых областей, выделены красным цветом. В случае использования лексикографического метода и упорядочения наблюдаемых переменных по убыванию их значимости, согласно формуле (1) будет выбран вариант v3, выделенный зеленым цветом. В случае использования мажоритарного метода, согласно формуле (2) будет выбран вариант v1, выделенный желтым цветом.
В табл. 2 приведены результаты эксперимента для задачи моделирования распределенной вычислительной среды [6]. В случае использования лексикографического метода и упорядочения наблюдаемых переменных по убыванию их значимости, согласно формуле (1) будет выбран вариант v2, выделенный зеленым цветом. В случае использования мажоритарного метода, согласно формуле (2) также будет выбран вариант v2.
Таблица 1
Результаты вычислительного эксперимента 1
|
Наблюдаемая переменная |
Критерий качества |
Область допустимых значений |
Варианты значений наблюдаемых переменных |
||||
|
v1 |
v2 |
v3 |
v4 |
v5 |
|||
|
y1 |
→ max |
∀n > 0, n ∈ R |
1,04 |
1,06 |
1,09 |
1,09 |
1,11 |
|
y2 |
→ min |
∀n ≤ 1, n ∈ R |
0,81 |
0,88 |
0,94 |
1,08 |
1,18 |
|
y3 |
→ max |
∀n > 0, n ∈ R |
0,23 |
0,18 |
0,15 |
0,01 |
–0,07 |
|
y4 |
→ max |
∀n > 0, n ∈ R |
28,40 |
20,45 |
15,96 |
0,93 |
–5,93 |
|
y5 |
→ min |
∀n ≤ 0,3, n ∈ R |
0,28 |
0,29 |
0,30 |
0,31 |
0,32 |
|
y6 |
→ min |
∀n ≤ 5, n ∈ R |
4,86 |
2,54 |
2,02 |
1,96 |
1,95 |
Таблица 2
Результаты вычислительного эксперимента 2
|
Наблюдаемая переменная |
Критерий качества |
Область допустимых значений |
Варианты средних значений наблюдаемых переменных |
|
|
v1 |
v2 |
|||
|
y1 |
→ min |
∀n ≥ 0, n ∈ R |
4,10 |
3,20 |
|
y2 |
→ min |
∀n ≥ 0, n ∈ R |
4106,84 |
3208,47 |
|
y3 |
→ min |
∀n ≥ 0, n ∈ R |
89 |
37 |
|
y4 |
→ min |
∀n ≥ 0, n ∈ R |
23 |
0 |
Заключение
В статье рассмотрена проблема управления сложной системой, связанная с многокритериальным выбором управляющих воздействий. Для ее решения сформулирована постановка задачи и построена соответствующая модель на основе методологии многокритериального выбора. Предложен новый алгоритм многокритериального выбора управляющих воздействий, ориентированный на поддержку принятия решений в процессе управления сложной системой. Алгоритм реализует эффективные операции оценки и выбора результатов имитационного моделирования исследуемой системы.
Исследование выполнено при финансовой поддержке РФФИ, проект № 15-29-07955-офи_м.
Рецензенты:
Опарин Г.А., д.т.н., профессор, зам. директора, ФГБУН «Институт динамики систем и теории управления им. В.М. Матросова» СО РАН, г. Иркутск;
Лакеев А.В., д.ф.-м.н., профессор, ведущий научный сотрудник, ФГБУН «Институт динамики систем и теории управления им. В.М. Матросова» СО РАН, г. Иркутск.