Использование непосредственных преобразователей электрической энергии (НПЭ) для управления напряжением, током и мощностью основано на импульсной, релейной либо комбинированной дискретизации коэффициентов передачи мощности [1–9]. В данной работе рассмотрим моделирование работы НПЭ с импульсным регулятором на базе широтно-импульсной модуляции (ШИМ).
Решение задачи математического моделирования НПЭ на базе существующих подходов осложняется факторами, связанными с наличием множества различных структур и большим числом задаваемых параметров. Данные подходы, предполагающие моделирование каждого переключающего элемента (ПЭ), требуют задания множества возможных состояний каждого из них. При непрерывном режиме работы число возможных состояний НПЭ определяется выражением
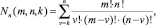 (1)
(1)
где m – число входных фаз; n – число выходных фаз; k – минимально возможное число фаз выходного напряжения.
Для НПЭ с n = 3 и m = 3 количество используемых состояний в соответствии с (1) при непрерывном режиме работы равно
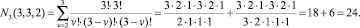
В работе рассмотрен предложенный авторами численный метод математического моделирования НПЭ с широтно-импульсным регулятором напряжения, в основе которого лежит предложенный авторами метод моделирования, основанный на представлении выходного напряжения НПЭ в виде единственного гармонического колебания с дискретно управляемой начальной фазой [2]. Принцип ШИМ применительно к НПЭ с искусственной коммутацией состоит в периодическом подключении на активный интервал времени Ta входного напряжения заданной фазы и в периодическом отключении на время пассивного интервала Tп.
Система поступающих на вход НПЭ напряжений включает m фаз
Ui(ωВХt) = Um sin(ωВХt – φi), 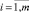 (2)
(2)
где Ui(ωВХt) – мгновенное значение входного напряжения; Um – амплитудное значение входного напряжения; ωВХ – круговая частота; φi – фазовый сдвиг.
В каждый момент времени на выход НПЭ с раздельным управлением подаётся только одна из множества поступающих на вход ЭДС, и формируется напряжение с амплитудным и мгновенным значениями Um2 и Ui(ωВЫХt), фазовым сдвигом φi, количеством фаз n и круговой частотой ωВЫХ.
Гармоническое колебание с дискретно управляемой начальной фазой представим выражением
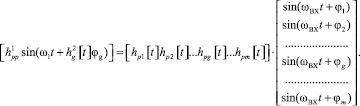 (3)
(3)
Процедуру непосредственного преобразования электрической энергии n-фазного НПЭ с раздельным управлением на основе предлагаемого метода и выражений (2) и (3) зададим моделью в матричной форме:
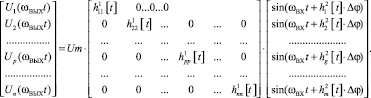 (4)
(4)
Переключающие функции, задающие возможные способы управления НПЭ в (4) с использованием однополярной ШИМ, представим выражениями
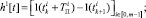
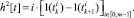
Блок-схемы алгоритмов формирования кривых выходного напряжения НПЭ при использовании однополярной ШИМ отражены на рис. 1–2.
При моделировании НПЭ с использованием двухфазной ШИМ переключающая функция амплитуды равна единице, а переключающую функцию фазы представим выражением
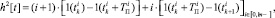 (5)
(5)
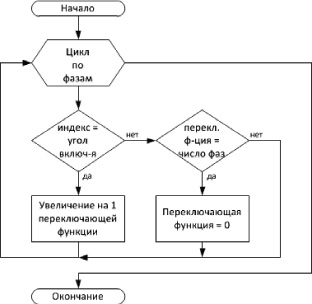
а
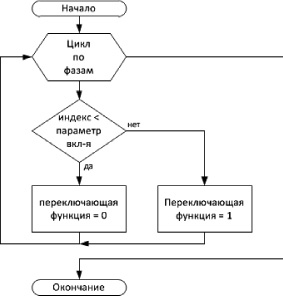
б
Рис. 1. Алгоритм моделирования НПЭ с однополярной ШИМ: а – формирование переключающей функции начальной фазы; б – изменение переключающей функции амплитуды
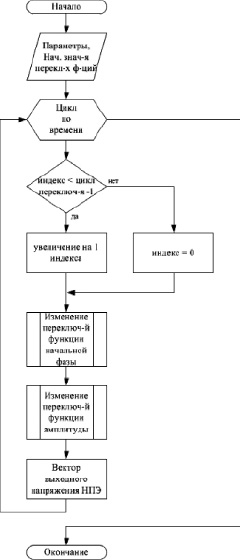
Рис. 2. Алгоритм основного цикла моделирования выходного напряжения НПЭ
Блок-схема алгоритма формирования переключающей функции начальной фазы при использовании двухфазной ШИМ (5) показана на рис. 3.
Результаты моделирования НПЭ c однополярной ШИМ на основе предложенного численного метода в среде Mathcad показаны на рис. 4. Для параметров системы приняты значения: входная частота f = 50 Гц, число фаз входного напряжения m = 9, фазовый угол включения тиристоров α = 0 эл. град. На рисунке представлены: XA – выходное напряжение в фазе А.
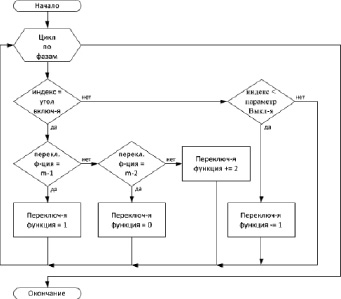
Рис. 3. Алгоритм формирования переключающей функции начальной фазы для двухфазной ШИМ
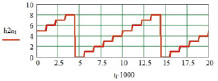
а
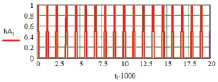
б
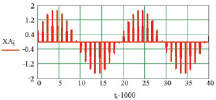
в
Рис. 4. Результаты моделирования при Tа = 0,25 Tп (однополярная ШИМ): а – переключающая функция фазы; б – переключающая функция амплитуды; в – выходное напряжение НПЭ в фазе А
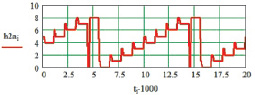
а
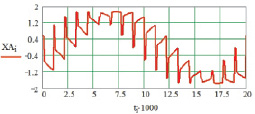
б
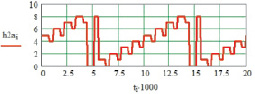
в
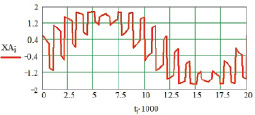
г
Рис. 5. Результаты моделирования НПЭ для двухфазной ШИМ: а – переключающая функция фазы (Tа = 0,25 Tп); б – выходное напряжение в фазе А (Tа = 0,25 Tп); в – переключающая функция фазы (Tа = 4 Tп), г – выходное напряжение в фазе А (Tа = 4 Tп)
Результаты моделирования НПЭ c двухфазной ШИМ на основе предложенного численного метода в среде Mathcad показаны на рис. 5. Для параметров системы приняты значения: входная частота f = 50 Гц, число фаз входного напряжения m = 9, фазовый угол включения тиристоров α = 0 эл. град. На рисунке представлены: XA – выходное напряжение в фазе А.
Таким образом, разработанный численный метод моделирования НПЭ с широтно-импульсной модуляцией обеспечивает сокращение объёма задаваемых исходных данных и упрощение компьютерного моделирования управляемых вентильно-электромеханических систем. Повышение эффективности моделирования достигается посредством сокращения до минимума количества моделируемых структур НПЭ и количества задаваемых параметров. Разработанный метод рекомендуется для компьютерного моделирования при исследовании как однодвигательных, так и многодвигательных многосвязных вентильно-электромеханических систем.
Рецензенты:
Бутаев М.М., д.т.н., профессор, учёный секретарь открытого акционерного общества «Научно-производственное предприятие “Рубин”, г. Пенза;
Зинкин С.А., д.т.н., профессор кафедры «Вычислительная техника», ФГБОУ ВПО «Пензенский государственный университет», г. Пенза.



