Важнейшим свойством дискретной системы, присущим всей системе, а не только отдельным её траекториям, является устойчивость. Известно [8], что исследование устойчивости решений нелинейного разностного уравнения сводится к выяснению расположения корней характеристического полинома соответствующего линеаризованного уравнения. При этом особую сложность представляет изучение критических случаев (называемых также граничной устойчивостью), когда некоторые корни характеристического полинома на комплексной плоскости попадают на единичную окружность [1, 3, 7].
Изучение критических случаев в теории устойчивости напрямую связано с исследованием границы области асимптотической устойчивости в пространстве параметров. Устойчивость в критических случаях изучена для непрерывных систем [1], но мало исследована для дискретных систем. Нашей целью является восполнение этого пробела для случая дискретной системы третьего порядка, описываемой характеристическим уравнением
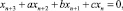(1)
где a, b, c ∈ R. Уравнение (1) называется устойчивым, если все его решения ограничены, и асимптотически устойчивым, если все его решения стремятся к нулю при n → ∞.
В работе [5] изучено более простое, чем (1), уравнение второго порядка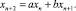 
Его область устойчивости в плоскости параметров a, b ∈ R такова: 
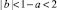. В [5] указаны участки границы этой области, на которых возникают различные типы решений: циклы, предельные циклы, псевдошумовые решения. Уравнения и системы третьего порядка в непрерывном случае изучались в [2, 7], а в дискретном – в [9, 6]. В [9] для уравнения (1) получены достаточные условия колебательности – неколебательности решений в виде ограничений на коэффициенты уравнения. Для близкого к (1) уравнения 
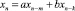с запаздываниями m, k ∈ N в [4] получено полное описание области асимптотической устойчивости в пространстве параметров a, b, k, m.
В настоящей работе мы полностью описываем асимптотическое поведение решений уравнения (1) при n → ∞, когда значения коэффициентов уравнения (1) находятся на границе его области устойчивости.
Граница области асимптотической устойчивости уравнения (1)
Известно, что нулевое решение уравнения (1) асимптотически устойчиво тогда и только тогда, когда все корни его характеристического полинома
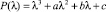(2)
по модулю меньше единицы. С помощью известного алгебраического критерия устойчивости Шура – Кона в [3] приведены необходимые и достаточные условия расположения всех корней характеристического полинома (2) внутри единичной окружности в виде системы ограничений на коэффициенты:
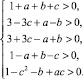
Эти же ограничения приводятся в [8] в преобразованном виде:
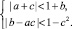
Анализируя эти системы, область асимптотической устойчивости уравнения (1) можно записать в виде, удобном для графического изображения области и ее границ:
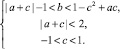(3)
Область асимптотической устойчивости уравнения (1) в пространстве коэффициентов a, b, c ∈ R изображена на рисунке. Она представляет собой тело, ограниченное гиперболическим параболоидом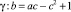 
и двумя плоскостями
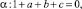
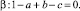
Область асимптотической устойчивости имеет ось симметрии – ось Ob.
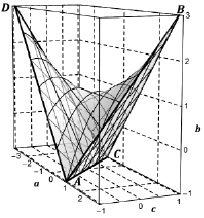
Область асимптотической устойчивости уравнения (1)
Границу области асимптотической устойчивости уравнения (1) образуют четыре вершины: A(1, –1, –1), B(3, 3, 1), C(–1, –1, 1), D(–3, 3, –1), пять ребер: AC (α ∩ β), AD и CD (α ∩ γ), AB и CB (β ∩ γ), две грани ACD и ABC и гиперболический параболоид γ.
Свойства характеристического полинома и асимптотическое поведение решений уравнения (1) на границе области асимптотической устойчивости
В этом пункте мы указываем свойства корней характеристического полинома (2) и асимптотическое поведение решений уравнения (1) на каждом участке границы области асимптотической устойчивости.
1. В точке A(1, –1, –1) имеем
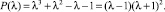
Все корни характеристического полинома P(λ) по модулю равны 1, причем λ = –1 – корень кратности 2. Тогда общее решение уравнения (1) имеет вид
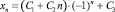
и в общем случае является неограниченным.
2. В точке C(–1, –1, 1) имеем
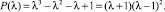
Все корни характеристического полинома P(λ) по модулю равны 1, причем λ = 1 – корень кратности 2. Тогда общее решение уравнения (1) имеет вид
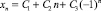
и в общем случае является неограниченным.
3. В точке B(3, 3, 1) имеем
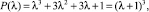
т.е. λ = –1 – корень кратности 3. Общее решение имеет вид
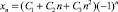
и в общем случае неограниченно.
4. В точке D(–3, 3, –1) имеем
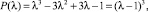
т.е. λ = 1 – корень кратности 3. Общее решение имеет вид
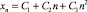
и в общем случае неограниченно.
5. На ребре
имеем
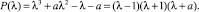
Все корни характеристического полинома P(λ) действительные и простые, причем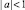 
. Общее решение уравнения (1) имеет вид
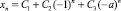
и является ограниченным, при этом в общем случае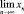 
не существует.
6. На ребре
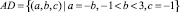
имеем
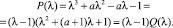
При –3 < a < 1 многочлен Q(λ) имеет два комплексно сопряженных корня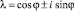 
, по модулю равных 1. Тогда общее решение уравнения (1) имеет вид
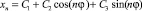
и является ограниченным при любых начальных условиях, при этом в общем случае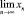 
не существует.
7. На ребре
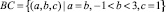
имеем
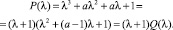
При –1 < a < 3 многочлен Q(λ) имеет два комплексно сопряженных корня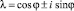 
, по модулю равных 1. Тогда общее решение уравнения (1) имеет вид
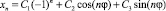
и является ограниченным, при этом в общем случае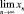 
не существует.
8. На ребре
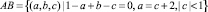
имеем
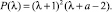
Все корни характеристического полинома P(λ) действительные, при этом λ = –1 – корень кратности 2, а при 1 < a < 3 модуль третьего корня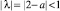 
. Тогда общее решение уравнения (1) имеет вид
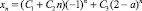
и в общем случае не является ограниченным.
9. На ребре
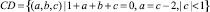
имеем
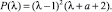
Все корни характеристического полинома P(λ) действительные, при этом λ = 1 – корень кратности 2, а при –3 < a < –1 модуль третьего корня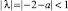 
. Тогда общее решение уравнения (1) имеет вид
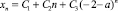
и в общем случае не является ограниченным.
10. Во внутренних точках треугольника
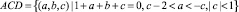
имеем
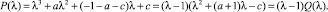
При c – 2 < a < –c имеем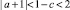 
. Тогда очевидно, что многочлен Q(λ) при (a + 1)2 + 4c > 0 имеет пару действительных корней
,
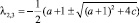по модулю меньших 1, при (a + 1)2 + 4c < 0 имеет пару комплексно сопряженных корней
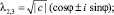
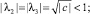
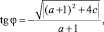
а при (a + 1)2 + 4c = 0 – действительный корень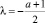 
кратности 2, по модулю меньший 1. Получаем, что общее решение уравнения (1) имеет вид
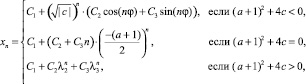
и является ограниченным, при этом в общем случае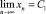 
.
11. Во внутренних точках треугольника
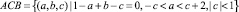
имеем
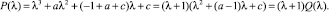
При –c < a < c + 2 имеем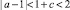 
. Тогда очевидно, что многочлен Q(λ) при (a – 1)2 – 4c > 0 имеет пару действительных корней 
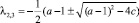, по модулю меньших 1, при (a – 1)2 – 4c < 0 имеет пару комплексно сопряженных корней
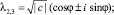
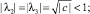
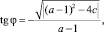
а при (a – 1)2 – 4c = 0 действительный корень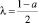 
кратности 2, по модулю меньший 1. Получаем, что общее решение уравнения (1) имеет вид
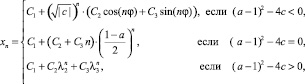
и является ограниченным, при этом в общем случае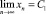 
.
12. В точках, лежащих на гиперболическом параболоиде b = 1 – c2 + ac, в области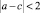 
, 
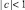имеем
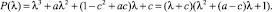
Характеристический полином P(λ) имеет один действительный корень λ = –c,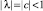 
и пару комплексно сопряженных корней
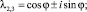
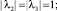
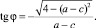
Тогда общее решение уравнения (1) имеет вид
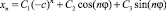
и является ограниченным при любых начальных условиях, при этом в общем случае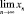 
не существует.
Выводы
На каждом из выделенных участков границы области устойчивости решения уравнения (1) обладают следующими особенностями асимптотического поведения.
В каждой из четырех вершин A, B, C, D в общем случае решения не ограничены и имеют полиномиальный рост, поэтому система (1) неустойчива. На рёбрах AC, AD, BC все решения ограничены, причем решения могут быть чисто периодическими, поэтому система (1) устойчива (не асимптотически). На ребрах AD и BC возможны так называемые псевдошумовые решения. На рёбрах AB и CD в общем случае решения не ограничены и имеют рост линейный по n, поэтому система (1) неустойчива.
Во внутренних точках граней ACB и ACD все решения ограничены, система устойчива (не асимптотически). В общем случае в указанной области решения имеют вид затухающих колебаний. В точках, лежащих на гиперболическом параболоиде, все решения ограничены, поэтому система (1) устойчива (не асимптотически). В общем случае в указанной области решения являются колебательными. Здесь возникают устойчивые циклы и псевдошумовые решения.
Заключение
Мы сделали полный анализ асимптотических свойств систем третьего порядка, когда их параметры находятся на границе области устойчивости. При специальном выборе начальных условий (посредством обнуления констант при неограниченных слагаемых в формуле общего решения) в исследованных областях, где диагностирована неустойчивость общего решения, можно выделить ограниченные или даже сходящиеся к нулю решения. Например, в п. 9 раздела «Свойства характеристического полинома и асимптотическое поведение решений уравнения (1) на границе области асимптотической устойчивости» настоящей статьи, если (a + 2)x0 – (a + 1)x1 – x2 = 0, то в общем решении xn = C1 + C2n + C3(–2–a)n имеем C2 = 0 и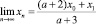 
. Поиск областей в пространстве начальных значений, которые дают ограниченные решения (проблема частичной устойчивости), требует отдельного тщательного исследования.
Работа поддержана грантом № 2807 Министерства образования России.
Рецензенты:
Дильман В.Л., д.ф.-м.н., профессор, заведующий кафедрой прикладной математики, ФГБОУ ВПО «Южно-Уральский государственный университет» (национальный исследовательский университет)», г. Челябинск;
Карачик В.В., д.ф.-м.н., профессор кафедры математического и функционального анализа, ФГБОУ ВПО «Южно-Уральский государственный университет» (национальный исследовательский университет)», г. Челябинск.