Многомерные корреляционные данные с учетом поляризационных характеристик комбинационного рассеивания света (КРС) или рамановской спектроскопии позволяют значительно увеличить достоверность идентификации при контроле наночастиц, находящихся на волокнах текстильных материалов. Проведенные работы [1–8] позволяют оценить наличие наночастиц на поверхности таких материалов, но определять режимы нанесения наночастиц серебра на материалы и особенно изменения их количества при эксплуатации затруднено из-за малого количества таких наночастиц.
Предлагаемые исследования позволяют с высокой достоверностью различить текстильные волокна, покрытые наночастицами серебра или не покрытые наночастицами серебра, по поляризационным характеристикам рамановских спектров с использованием многомерных методов оценки достоверности и векторно-матричной корреляции. Цель работы. Проведение динамического статистического моделирования случайного процесса изменения экспериментальных параметров наночастиц серебра по времени эксплуатации совместно с автокорреляционными функциями и взаимозависимыми параметрами по заданной корреляционной матрице и многомерной автокорреляцией. Сложность такого моделирования заключается именно в необходимости получения случайных значений при различных комбинациях параметров корреляционных матриц.
Материалы и методы исследования
При проведении эксперимента выбраны полиэфирные (ПЭ) волокна, на которые были нанесены наночастицы серебра из коллоидного раствора наночастиц серебра AgБион (ТУ 2499-003-44471019-2006, концерн «Наноиндустрия»). Измерения были проведены в лаборатории нанотехнологий ЮЗГУ на сканирующем зондовом микроскопе (СЗМ) при различной поляризации луча, в результате чего были получены цифровые и графические показатели рамановских спектров.
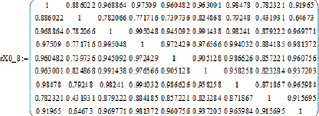
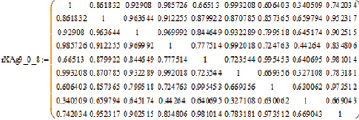
Математическая обработка осуществлялась с применением математической программы Matchad. При этом были выявлены параметры распределений и получены корреляционные матрицы с учетом поляризации излучения по X и по Y, которые выборочно представлены на рис. 1.
Предлагаемый в работе метод многомерной корреляционной оценки наличия наночастиц серебра на полиэфирных волокнах с использованием векторно-матричного моделирования состоит из нескольких этапов. Вначале формируется общая корреляционная матрица для полной генерации данных на основе исходных матриц, полученных на предыдущем этапе:
RX1_1:= augment(rXAg9_0_8, rXYAg9_0_8, rY0_8XAg9_0_8, rY1); (1)
RX1_2:= augment(rXYAg9_0_8T, rYAg9_0_8, rX1, rX0_8YAg9_0_8); (2)
RX1_3:= augment(rY0_8XAg9_0_8T, rX1T, rX0_8, rXY1); (3)
RX1_4:= augment(rY1T, rX0_8YAg9_0_8T, rXY1T, rY0_8); (4)
RX1_4:= stack(RX1_1, RX1_2, RX1_3, RX1_4). (5)
 а
а
 б
б
Рис. 1. Корреляционные матрицы рамановских поляризационных спектрограмм полиэфирных волокон после сушки в естественных условиях: а – поляризация лазера поперек волокон с наночастицами серебра; б – поляризация лазера поперек волокон без наночастиц серебра
Тогда тестовая общая размером 38×38 корреляционная матрица примет вид
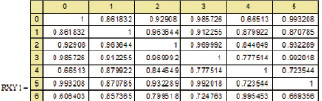 (6)
(6)
Генерация случайных значений проводится по нормальному закону и матрице RXY1, для чего используется встроенная функция MathCad Edition 11:
GEN1<k> := rnorm(n, M, λXk0,5), (7)
где λXk – вектор собственных чисел корреляционной матрицы; n – количество случайных данных в одном векторе; М – математическое ожидание.
При этом вектор собственных чисел общей корреляционной матрицы определяется по выражению
λX:= eigenvals(RXY1). (8)
Так как сгенерированные по (7) случайные значения обладают некоторой корреляцией, негативно сказывающейся на точности моделирования, то необходимо привести их к некоррелированному виду, для чего используется специальная программа, разработанная в рамках данного научного исследования в среде MathCad Enterprise Edition:
i := 0…35; j:= 0…35;
RGEN1 i,j:= corr(GEN<i>, GEN<j>);
UR:= eigenvecs(RGEN1) λ1:= eigenvals(RGEN1);
GEN2:= GEN1 NZ2:= GEN2⋅URT;
RNZ2i,j:= cvar(NZ2<i>, NZ2<j>) FUND:= eigenvecs(RNZ2);
NEZ:= NZ2⋅FUND RNEZ2i,j:= corr(NEZ<i>, NEZ<j>). (9)
Полученные таким преобразованием (9) значения данных моделирования обладают корреляцией, стремящейся к нулю (10).
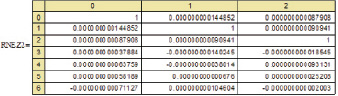 (10)
(10)
Из (10) видно, что полученные статистическим моделированием некоррелированные случайные данные обладают точностью до 10–10, что значительно превосходит заданную точность исходной общей корреляционной матрицы 10–6 (6).
На следующем этапе проводится коррекция полученных некоррелированных данных моделирования по среднему квадратическому отклонению и собственным числам:
sNEZi:= stdev(NEZ<i>) NEZ<k>:= NEN<k>⋅λXk0,5/sNEZk;
sNEZi:= stdev(NEZ<i>) NEZ<k>:= NEN<k>⋅λXk0,5/sNEZk;
sNEZi:= stdev(NEZ<i>). (11)
Далее преобразуем некоррелированные значения по (12) через фундаментальную матрицу UR корреляционной матрицы RXY1 в коррелированные:
UR:= eigenvecs(RXY1) ZAV:= NEZ⋅URT;
RZ i,j:= corr(ZAV<i>, ZAV<j>). (12)
Вычислим корреляционную матрицу для коррелированных данных RZ для оценки достоверности полученного результата
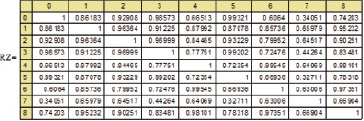 (13)
(13)
Из (13) видно, что полученные статистическим моделированием коррелированные случайные данные обладают корреляцией, равной исходной общей корреляционной матрицы (6), с точностью до 10–6. Однако значения матрицы RZ из-за особенностей вычисления нормированы по 1 относительно среднего квадратического отклонения.
Приведем в соответствие значения реальных измерений по матрице RZ, по средним квадратическим отклонениям и по математическим ожиданиям:
Dr ⟨n⟩ := ZAV⟨n⟩⋅σΔX_9n + MENX_9n;
Tr⟨n⟩:= ZAV⟨n+18⟩ ⋅σΔXn + MENXn; (14)
Dry⟨n⟩ := ZAV⟨n+9⟩ ⋅σΔY_9n + MENY_9n;
Try⟨n⟩:= ZAV⟨n+27⟩ ⋅σΔYn + MENYn. (15)
Результаты исследования и их обсуждение
Вычислим для подтверждения корреляционные матрицы RDr; RTr и среднее квадратическое отклонение между столбцами этих матриц sDr, sTr:
RDr n, m:= corr(Dr⟨n⟩, Dr⟨m⟩ ); sDrn:= stdev(Dr⟨n⟩).

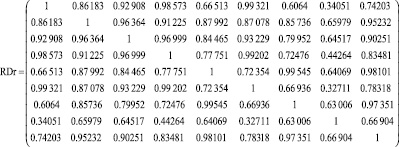 (16)
(16)
RTr n, m:= corr(Tr⟨n⟩ , Tr⟨m⟩ ); sTrn:= stdev(Tr⟨n⟩ ).

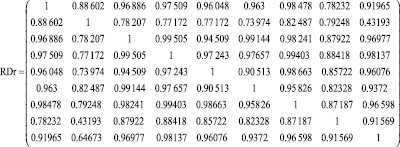 . (17)
. (17)
Из (16) и (17) видно, что корреляция смоделированных случайных значений соответствует корреляции исходных данных (рис. 1 а, б). Среднеквадратические отклонения смоделированных значений также совпадают с исходными данными.
Возможно моделирование параметров измерений для различных значений элементов спектральных составляющих многомерных поляризационных корреляционных матриц типа (16) и (17) с учетом различных значений параметров многомерных законов распределения. Однако следует учесть, что для нормальных законов распределения значений параметров спектральных составляющих получают самую высокую точность моделирования.
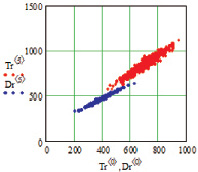
Для оценки достоверности была предложена методика определения взаимного перекрытия данных. На рис. 2 выборочно представлены смоделированные корреляционные зависимости.
При оценке достоверности по экспериментальным одномерным векторам получены следующие значения:
pX12T = (0.98153 0.92831 0.98894 0.99789 0.99125 0.99689 0.98682 0.99932 0.99910). (18)
Проверка по смоделированным одномерным данным показала следующую достоверность при генерации 576 значений (рис. 2, в):
pDr⟨5⟩ = 1 – 3/576 = 0.99479;
pTr⟨5⟩ = 1 – 2/576 = 0.99653;
pDr⟨0⟩ = 1 – 8/576 = 0.98611;
pTr⟨0⟩ = 1 – 8/576 = 0.98611. (19)
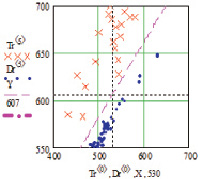
По рис. 2, г, с использованием смоделированные одномерных данных проверка показала следующую достоверность при генерации 576 значений:
pDr⟨5⟩ = 1 – 3/576 = 0.99479;
pTr⟨5⟩ = 1 – 3/576 = 0.99479;
pDr⟨1⟩ = 1 – 47/576 = 0.91840;
pTr⟨1⟩ = 1 – 48/576 = 0.91667. (20)
При рассмотрении двумерной зависимости с корреляцией по рис. 2, в оценить достоверность для первого пика при учете шестого не представилась возможность из-за малого количества сгенерированных значений – необходимо сгенерировать не 576, а 20000 значений.
При генерации 576 значений (рис. 2, г) проверка по смоделированным двумерным данным показала следующую достоверность:
pTr⟨5⟩ Tr⟨1⟩ = 1 – 2/576 = 0.99653;
pDr⟨5⟩ Dr⟨1⟩ = 1 – 2/576 = 0.99653. (21)
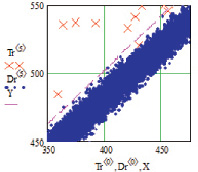
Проверка по смоделированным двумерным данным показала следующую достоверность при генерации 20000 значений (рис. 2, д):
pTr⟨5⟩ Tr⟨0⟩ = 1 – 2/20000 = 0.9999;
pDr⟨5⟩ Dr⟨0⟩ = 1 – 2/20000 = 0.9999. (22)
Здесь видно, что предложенный метод дает существенный выигрыш в оценке достоверности определения режимов нанесения наночастиц серебра на волокна.
 а
а 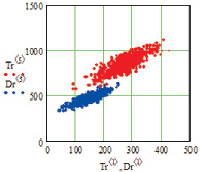 б
б
 в
в 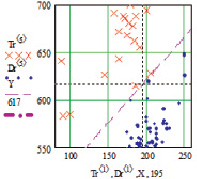 г
г
 д
д 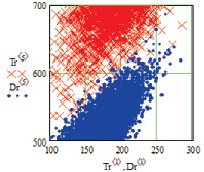 е
е
Рис. 2. Двумерные смоделированные корреляционные зависимости рамановских поляризационных спектрограмм наночастиц серебра на полиэфирных волокнах с поляризацией поперек волокон: а, б – общий вид при генерации n = 576 данных; в, г – фрагмент для определения взаимного перекрытия данных для определения достоверности p5_1 = 0.9965 при пересечении 2 данных с генерацией n = 576; д, е – фрагмент для определения взаимного перекрытия данных для определения достоверности p5_0 = 0.9990 при пересечении 2 данных с генерацией n = 20000
Выводы
Таким образом, на основании проведенных исследований был предложен метод многомерной оценки наличия наночастиц серебра на волокнах с использованием векторно-матричного моделирования при генерации достаточно большого диапазона значений с сохранением законов распределений и корреляционных многомерных зависимостей между данными; проведена оценка достоверности при определении количества пересечений многомерных распределений рамановских спектров волокна, установлено, что одномерная оценка достоверности дает диапазон 0,92831–0,99932, а многомерная – до 0,9999.
Рецензенты:
Сотников В.В., д.т.н., доцент, профессор кафедры «Электроснабжение», Юго-Западный государственный университет, г. Курск;
Кузьменко А.П., д.ф.-м.н., профессор, директор регионального центра нанотехнологий, Юго-Западный государственный университет, г. Курск.



