Bryukhanova T.N. 1
Ivanova G.D. 2
Kuzin A.A. 2
Rekunova N.N. 2
1 Pacific National University
2 Far Eastern State Transport University
A light induced relief modulation is used to record optical information and to create the managed thermo-optical deflectors. In this paper it was investigated theoretically a thermo-mirror based on a thin polymer film. When exposed to a beam of radiation with sinusoidal spatial distribution of intensity the film heating leads to the formation of appropriate relief on its surface. The model of the phenomenon was proposed, in which light induced thin film extension leads to its appropriate deformation. It were analyzed the spatial-temporal characteristics of the relief nonlinearity using the decision of the two-dimensional thermal task of the thermal expansion of the film. The heat task is done under the assumption that the heat sink from the surface film is convective and heat transfer along the film is negligible. It was suggested to use a thermo-mirror for compensation of thermal lenses in thin-layer liquid-phase nonlinear-optical elements.
dynamic holography
relief holograms
the thermal expansion of the medium
phase conjugation
1. Betin A.A. Otrazhenie izluchenija SO2-lazera pri vyrozhdennom chetyrjohvolnovom vzaimodejstvii v zhidkostjah / A.A. Betin, E.A. Zhukov, O.V. Mitropolskij.Kvantovaja jelektronika. 1985. t. 12. no. 9. рр. 1890.
2. Golubcov A.A. Obrashhenie volnovogo fronta pri svetoinducirovannom profilirovanii formy poverhnosti pogloshhajushhego veshhestva /A.A.Golubcov, N.F. Pilipeckij, A.N. Sudarkin, V.V. Shkunov.Kvantovaja jelektronika. 1981. T. 8.
3. Ivanov V.I. Vlijanie termodiffuzii na termolinzovyj otklik v zhidkofaznoj dispersnoj srede / V.I. Ivanov, G.D. Ivanova, V.K. Khe. Fiziko-himicheskie aspekty izuchenija klasterov, nanostruktur i nanomaterialov, mezhvuz. sb. nauch. tr. / pod obshhej redakciej V.M. Samsonova, N.Ju. Sdobnjakova. Tver: Tver. gos. un-t, 2013. Vyp. 5. рр. 112–115.
4. Ivanov V.I. Termoinducirovannye mehanizmy zapisi dinamicheskih gologramm. Monografija. Vladivostok: Dalnauka, 2006. 143 р.
5. Ivanov V.I., Ivanova G.D., Khe V.K. Teplovoe samovozdejstvie izluchenija v tonkoslojnoj zhidkofaznoj srede. Sovremennye problemy nauki i obrazovanija. 2014. no. 6. URL: www.science-education.ru/120-17046.
6. Ivanov V.I., Illarionov A.I., Korosteleva I.A. Obrashhenie volnovogo fronta nepreryvnogo izluchenija v uslovijah silnogo samovozdejstvija.Pisma v «Zhurnal tehnicheskoj fiziki». 1997. T. 23. no. 15. ррS. 60–63.
7. Ivanov V.I., Karpec Ju.M., Okishev K.N., Livashvili A.I. Termodiffuzionnyj mehanizm prosvetlenija dvuhkomponentnoj sredy lazernym izlucheniem. Izvestija Tomskogo politehnicheskogo universiteta. 2007. T. 311. no. 2. рр. 39–42.
8. Ivanov V.I., Kuzin A.A., Livashvili A.I., Khe V.K. Dinamika svetoinducirovannoj teplovoj linzy v zhidkofaznoj dvuhkomponentnoj srede. Nauchno-tehnicheskie vedomosti Sankt-Peterburgskogo gosudarstvennogo politehnicheskogo universiteta. Fiziko-matematicheskie nauki. 2011. T.4. no. 134. рр. 44–46.
9. Ivanov V.I., Livashvili A.I., Brjuhanova T.N., Rekunova N.N. Prostranstvenno-vremennye harakteristiki termoinducirovannogo mehanizma zapisi relefnyh dinamicheskih gologramm. Vestnik Tihookeanskogo gosudarstvennogo universiteta. 2011. no. 1. рр. 065–068.
10. Ivanov V.I., Livashvili A.I. Jelektrostrikcionnyj mehanizm samovozdejstvija izluchenija v zhidkosti s nanochasticami. Vestnik Novosibirskogo gosudarstvennogo universiteta. Serija: Fizika. 2009. T. 4. no. 2. рр. 58–60.
11. Ivanov V.I., Livashvili A.I. Jeffekt Djufura v dispersnoj zhidkofaznoj srede v pole gaussova puchka. Fiziko-himicheskie aspekty izuchenija klasterov, nanostruktur i nanomaterialov, mezhvuz. sb. nauch. tr. / pod obshhej redakciej V. M. Samsonova, N.Ju. Sdobnjakova. Tver: Tver. gos. un-t, 2013. Vyp. 5. рр. 116–119.
12. Ivanov V.I., Livashvili A.I., Okishev K.N. Termodiffuzionnyj mehanizm izmenenija opticheskogo propuskanija dvuhkomponentnoj sredy. Izvestija vysshih uchebnyh zavedenij. Priborostroenie. 2008. T. 51. no. 3. рр. 50–53.
13. Livashvili A.I., Ivanova G.D., Khe V.K. Stacionarnyj termolinzovyj otklik nanozhidkosti. Fiziko-himicheskie aspekty izuchenija klasterov, nanostruktur i nanomaterialov, mezhvuz. sb. nauch. tr. / pod obshhej redakciej V. M. Samsonova, N.Ju. Sdobnjakova. Tver: Tver. gos. un-t, 2014. Vyp. 6. рр. 227–230.
14. Okishev K.N. Termodiffuzionnyj mehanizm nelinejnogo pogloshhenija suspenzii nanochastic / K.N. Okishev, V.I. Ivanov, S.V. Klimentev, A.A Kuzin, A.I. Livashvili. Optika atmosfery i okeana. 2010. T. 23. no. 2. рр. 106–107.
15. Ivanov V.I., Illarionov A.I., Korosteleva I.A. Technical Physics Letters. 1997. Vol. 23. n. 1. pp. 600–601.
Различные механизмы оптической нелинейности на поверхности раздела сред широко используются в динамической голографии для хранения и обработки оптической информации [1–4, 9]. При этом динамическая голограмма представляет собой решетку амплитудного френелевского коэффициента отражения r («поверхностную» голограмму). Соответствующий метод обращения волнового фронта излучения отражающей поверхностью (ОВФ-П) впервые предложен Б.Я. Зельдовичем с сотрудниками [2]. Особенность этого метода состоит в том, что здесь требуется только одна опорная волна Е0, которая записывает решетку δr, интерферируя с сигнальной волной Е3 (δr ~ Е0Е3), и одновременно дифрагирует на этой отражательной решетке. Фазовое сопряжение будет точным, если волновой фронт опорной волны совпадает с формой отражающей поверхности (которая может быть и неплоской).
В одной из первых экспериментальных работ по записи поверхностных динамических голограмм было использовано тепловое расширение среды [1]. Там же проведен анализ нелинейности для стационарного режима записи, а частотно-временные и пространственные характеристики нелинейности не исследованы.
Целью данной работы является исследование пространственно-временной зависимости коэффициента рельефной нелинейности, обусловленной тепловым расширением слоя среды.
Независимо от природы «поверхностной» нелинейности, ее можно описать, используя зависимость комплексного амплитудного коэффициента отражения от интенсивности 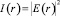 (в обозначениях работы [2]) падающего излучения:
(в обозначениях работы [2]) падающего излучения:
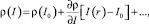 (1)
(1)
где r – радиус-вектор в плоскости раздела сред; I0 – среднее значение интенсивности излучения; 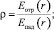
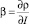 – коэффициент поверхностной нелинейности.
– коэффициент поверхностной нелинейности.
Пусть на зеркально отражающую поверхность падает строго нормально плоская волна E0exp(–ikz), под углом θ3 к нормали когерентная с ней слабая сигнальная волна E3 (рис. 1). В результате интерференции волн E0 и E3 коэффициент отражения становится промодулированным [2]:
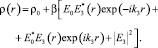 (2)
(2)
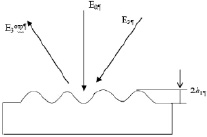
Cхема записи рельефной голограммы
Поглощение света с поперечно-неоднородным профилем интенсивности I(r) вызывает неоднородный прогрев поверхностных слоев материала зеркала. Из-за теплового расширения в максимуме интенсивности зеркало выпучивается навстречу пучку, т.е. образуется решетка рельефа [2]:
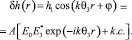 (3)
(3)
Для нахождения амплитуды рельефа сначала необходимо решить следующую двумерную нестационарную тепловую задачу:
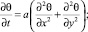 (4)
(4)
θ(x, y, t) = T(x, y, t) – T0, (5)
где T0 – начальная температура среды.
С граничными и начальными условиями
0 ≤ x < ℓ; –∞ < y < ∞; θ(x, y, 0) = 0; (6)
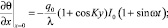
θ(x, y, ℓ) = 0, (7)
где K = kθ3 – волновой вектор интерференционной решетки; 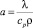 – температуропроводность среды; λ – коэффициент теплопроводности материала; cp и ρ – удельная теплоемкость и плотность среды соответственно.
– температуропроводность среды; λ – коэффициент теплопроводности материала; cp и ρ – удельная теплоемкость и плотность среды соответственно.
Удобно вести функцию V(x), удовлетворяющую уравнению
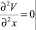 (8)
(8)
и условиям:
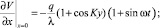
V(ℓ) = 0. (9)
Из равенств (8) и (9) можно найти вид функции V(x):
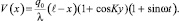 (10)
(10)
Решение исходной задачи ищем в виде
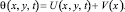 (11)
(11)
Подстановка (11) в (5) приводит к задаче вида
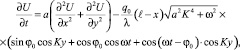 (12)
(12)
где 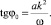
Соответствующие начальные и граничные условия будут иметь вид
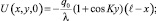
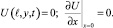 (13)
(13)
Используя функцию Грина [5] для задачи (12)–(13) и проводя соответствующие интегрирования, получим искомое выражение для температуры:
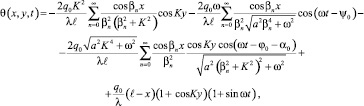
где 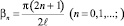
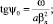
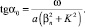
Модуляция рельефа определяется тепловым расширением среды:
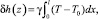 (14)
(14)
где γ – коэффициент линейного теплового расширения среды.
Учитывая, что 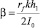 [2], найдем коэффициент поверхностной нелинейности, учитывая только переменную составляющую модуляции рельефа:
[2], найдем коэффициент поверхностной нелинейности, учитывая только переменную составляющую модуляции рельефа:
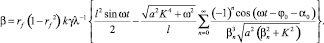 (15)
(15)
Полученное выражение показывает, как коэффициент рельефной нелинейности зависит от частоты модуляции падающего излучения и волнового вектора динамической голограммы. Проведенный анализ может представлять интерес для расчета пространственно-временных характеристик фазосопряженных зеркал, используемых в прикладных задачах нелинейной оптики [1–8], для компенсации термонаведенных искажений в нелинейных средах [10–15].
Рецензенты:
Карпец Ю.М., д.ф.-м.н., профессор кафедры «Физика и теоретическая механика», ФГБОУ ВПО «Дальневосточный государственный университет путей сообщения», г. Хабаровск;
Криштоп В.В., д.ф.-м.н., профессор кафедры физики, проректор по учебной работе, ФГБОУ ВПО «Дальневосточный государственный университет путей сообщения», г. Хабаровск.
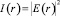 (в обозначениях работы [2]) падающего излучения:
(в обозначениях работы [2]) падающего излучения:
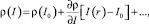 (1)
(1)
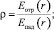
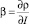 – коэффициент поверхностной нелинейности.
– коэффициент поверхностной нелинейности.
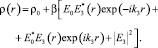 (2)
(2)

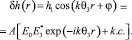 (3)
(3)
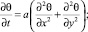 (4)
(4)
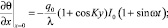
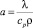 – температуропроводность среды; λ – коэффициент теплопроводности материала; cp и ρ – удельная теплоемкость и плотность среды соответственно.
– температуропроводность среды; λ – коэффициент теплопроводности материала; cp и ρ – удельная теплоемкость и плотность среды соответственно.
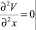 (8)
(8)
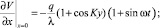
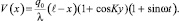 (10)
(10)
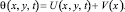 (11)
(11)
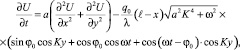 (12)
(12)
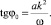
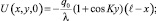
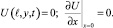 (13)
(13)
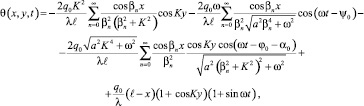
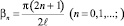
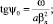
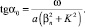
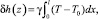 (14)
(14)
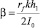 [2], найдем коэффициент поверхностной нелинейности, учитывая только переменную составляющую модуляции рельефа:
[2], найдем коэффициент поверхностной нелинейности, учитывая только переменную составляющую модуляции рельефа:
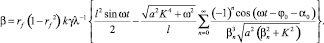 (15)
(15)



