Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Методы корреляционного анализа широко используются для исследования зависимостей в медицине, экономике и других областях деятельности человека. Универсальный математический аппарат позволяет применять корреляционный анализ в любой предметной области, таким образом, возможно его использование в электроэнергетике, например, для определения зависимостей с целью эффективного управления процессами. В работах [5, 6] рассматриваются подходы к минимизации потерь активной мощности, зависящей от показателей качества электроэнергии (ПКЭ), однако они базируются на разработке методов управления отдельными показателями, но не рассматривают улучшение показателей качества в комплексе. Например, в качестве целевой функции задается минимум отклонения напряжений и частоты от номинального значения, при этом не берутся во внимание суммарные потери, обусловленные неучтенными ПКЭ, которые, как правило, поддерживаются в сравнительно широкой области допустимых значений. Необходимо учитывать, что в сложноподчиненной структуре электроэнергетических систем ПКЭ могут зависеть друг от друга. При этом взаимная зависимость может быть как прямая, так и обратная, а следовательно, улучшение одного из показателей качества может не только приводить к улучшению других показателей, но и к их ухудшению.

Проблема управления ПКЭ является актуальной, особенно для промышленных предприятий, процесс производства которых беспрерывен, и любая остановка оборудования может привести к значительным потерям. Таким образом, возникает необходимость в исследовании функциональной взаимосвязи между показателями качества электроэнергии. Данное исследование позволит принимать решения по применению тех или иных средств, необходимых для улучшения качества электроэнергии.

Применение математических методов к анализу ПКЭ описано во многих работах, в частности [3, 7], однако в таких работах математические методы используются лишь для обработки результатов измерений, а не для определения влияния одних показателей на другие.

Основываясь на математических подходах по определению взаимосвязи между независимыми величинами, приведенных в [1], возможно создание методики, которая позволит, учитывая взаимосвязи, решить поставленную задачу оптимального управления несколькими показателями комплексно.

В качестве объекта исследования взаимосвязи были взяты протоколы измерений показателей качества электрической энергии предприятия нефтеперерабатывающей отрасли. В табл. 1 выборочно представлены результаты измерений (две секции шин ГПП, фаза A).

Построение системы управления ПКЭ должно включать в себя три основных этапа:

1. Установление самого факта наличия или отсутствия статистической связи между ПКЭ.

2. Прогноз значений результирующих зависимых ПКЭ по текущим параметрам режима и относительно друг друга.

3. Выявление причинных связей между ПКЭ, включая математическое описание, и управление значениями ПКЭ путем регулирования параметров режима.

Таблица 1

Показатели качества электрической энергии предприятия нефтеперерабатывающей отрасли

Можно заметить, что каждый следующий тип конечной цели включает в себя предыдущий: без наличия связи между величинами невозможно сделать прогноз значений зависимых переменных, в то же время без наличия прогнозных значений невозможно качественное регулирование выходных величин. Таким образом, для построения системы управления показателями качества электрической энергии необходимо начать с простого выявления взаимосвязи между отдельными парами показателей качества. Решение этой задачи производилось методами корреляционного анализа.

Проверка на соответствие выборки законам нормального распределения была проведена в соответствии с методикой, описанной в [2]. Анализ выборки снятых показателей качества показал, что данные не соответствуют законам нормального распределения, таким образом, к анализу зависимостей не может использоваться классический коэффициент Пирсона. Если выборки данных не соответствуют законам нормального распределения, то для анализа их взаимосвязи можно использовать коэффициенты ранговой корреляции Спирмэна или Кендалла. В совокупности данные коэффициенты более полно отражают реальную картину взаимодействия, коэффициент Кендалла более полно и детально анализирует связи между переменными, перебирая все возможные соответствия между парами значений, а коэффициент Спирмена более точно учитывает именно количественную степень связи между переменными.

Коэффициент корреляции Спирмэна вычисляется по формуле

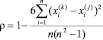, (1)

где 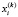, 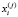ранги i-ой пары соответствующих переменных, n – количество пар переменных.

Однако, такая формула пригодна лишь для расчетов в случае отсутствия объединенных рангов в исследуемых ранжировках. Если в одной из переменных присутствует несколько одинаковых значений, то их ранги будут совпадать, в таком случае высчитываются поправочные коэффициенты:

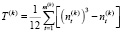, (2)

где 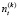– число элементов (рангов), входящих в t-ую группу неразличимых рангов, m^(k) – число групп неразличимых рангов у переменной X^(k).

Тогда формула коэффициента Спирмэна запишется следующим образом:

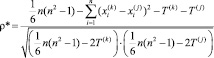. (3)

Таблица 2

Расчет коэффициента ранговой корреляции Спирмэна

Коэффициент ранговой корреляции Кендалла рассчитывается по формуле

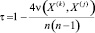, (4)

где 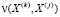– минимальное число обменов соседних элементов последовательности X(j), необходимое для приведения ее к упорядочению X(k).

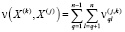, (5)

где

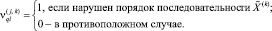
Если исследуемые данные повторяются (имеют одинаковые ранги), то в расчетах используется скорректированный коэффициент корреляции Кендалла:

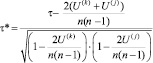, (6)

где коэффициент τ рассчитывается по формуле (4), поправочные величины U^(l) определяются следующим выражением:

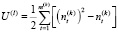, (7)

где 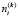– число элементов (рангов), входящих в t-ую группу неразличимых рангов, m^(k) – число групп неразличимых рангов у переменной x^(k).

Согласно формулам (3) и (6) был произведен расчет коэффициентов ранговой корреляции Спирмэна и Кендалла для следующих пар показателей качества электрической энергии:

1. Коэффициент искажения синусоидальности кривой напряжения K_UA – коэффициент n-й гармонической составляющей K_U(n).

2. Установившееся значение отклонения напряжения в режиме наибольших нагрузок δU_{у(А)б рнбн} – коэффициент несимметрии по обратной последовательности K_2U.

3. Установившееся значение отклонения напряжения в режиме наибольших нагрузок δU_{у(А)б рнбн} – коэффициент несимметрии по нулевой последовательности K_0U.

4. Установившееся значение отклонения напряжения в режиме наименьших нагрузок δU_{у(А)б рнмн} – коэффициент несимметрии по обратной последовательности K_2U.

5. Установившееся значение отклонения напряжения в режиме наименьших нагрузок δU_{у(А)б рнмн} – коэффициент несимметрии по нулевой последовательности K_0U.

6. Коэффициент несимметрии по нулевой последовательности K_0U – коэффициент искажения синусоидальности кривой напряжения K_UA.

7. Коэффициент несимметрии по обратной последовательности K_2U – коэффициент искажения синусоидальности кривой напряжения K_UA.

Данные пары показателей были выбраны в качестве начальных, поскольку между ними наиболее очевидна логическая связь, однако данный факт не всегда говорит о функциональной связи. Расчет был произведен для выборок длиной 96 и 97 строк. Расчетные данные приведены в табл. 2, 3.

Проверка статистической значимости коэффициентов была проведена критериям, приведенным в [4]. Результаты проверки приведены в табл. 2, 3. Для коэффициента Спирмэна гипотеза о наличии значимой корреляционной связи с вероятностью α выполняется при условии:

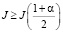, (8)

где α – доверительная вероятность события, принятая α = 0,99.

Для коэффициента ранговой корреляции Кендалла гипотеза о наличии значимой связи выполняется при выполнении условия:

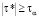, (9)

где τ_α – критическое значение, зависящее от количества строк в выборке и доверительной вероятности α.

Исходя из рассчитанных коэффициентов, можно сделать вывод о том, что умеренная связь (при коэффициентах Спирмэна, лежащих в пределах от 0,3 до 0,7) присутствует между следующими парами показателей:

1. Коэффициент искажения синусоидальности кривой напряжения K_UA – коэффициент n-й гармонической составляющей K_U(n).

Таблица 3

Расчет коэффициента ранговой корреляции Кендалла

2. Коэффициент несимметрии по нулевой последовательности K_0U – коэффициент искажения синусоидальности кривой напряжения K_UA.

3. Коэффициент несимметрии по обратной последовательности K_2U – коэффициент искажения синусоидальности кривой напряжения K_UA.

В случае, если коэффициент корреляции Спирмэна меньше 0,3 и статистическая значимость коэффициента не подтверждается, считается, что связь между величинами слабая, но возможно наличие нелинейной зависимости между этими показателями, что требует дополнительных исследований.

Расчет коэффициента Кендалла показал, что для всех выбранных пар показателей линейная связь будет умеренной, при этом статистически значимой.

В результате работы было выявлено, что взаимная зависимость ПКЭ не соответсвует закону нормального распределения, следовательно, для определения взаимозависимости между ПКЭ невозможно использование классического коэффициента корреляции, но допускается использовать коэффициенты ранговой корреляции Спирмэна и Кендалла.

Проведенный корреляционный анализ позволил проследить явно выраженную взаимную зависимость между ПКЭ, для 7 пар коэффициенты больше 0,3, что говорит о наличии умеренной линейной связи.

Изложенный аппарат является основой для разработки методики управления ПКЭ. В качестве следующего этапа будет производиться корректировка выявленной взаимосвязи и выведение функциональной зависимости между ПКЭ с учетом введения некоторого поправочного коэффициента, который будет зависеть от вида подключенной нагрузки.

Рецензенты:

Бочкарев С.В., д.т.н., доцент, профессор кафедры «Микропроцессорные средства автоматизации», ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь;

Казанцев В.П., д.т.н., доцент, профессор кафедры «Микропроцессорные средства автоматизации», ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.