Современные автоматизированные и автоматические системы управления технологическими процессами (АСУТП) ориентированы на реализацию предельного быстродействия отработки задающих и возмущающих воздействий. Это предопределено, с одной стороны, требованиями форсирования производительности технологических процессов с учетом заданных ограничений на значения переменных процесса, с другой – возросшими возможностями программно-технической реализации сложных нелинейных алгоритмов управления на основе микропроцессорных контроллеров и сервоприводов [1–3].
Выходной переменной той или иной локальной электромеханической системы управления (ЭМСУ) в составе АСУТП является, как правило, либо скорость, либо положение (угловые или линейные) некоторого рабочего органа. В общем же случае в ЭМСУ выделяют до четырех фазовых переменных с интегро-дифференцирующими зависимостями: положение, скорость, ускорение, рывок [1, 2, 4, 6]. Поскольку в соответствии с общеизвестными положениями теории управления [5] управлять объектами, содержащими интеграторы второго и более высокого порядка с контролем только выходной переменной, не представляется возможным из-за потери устойчивости, то применяют декомпозицию объекта и введение обратных связей по ряду промежуточных переменных. Это позволяет организовать оптимальное в некотором смысле подчиненное регулирование координат электроприводов и, как следствие, компромиссное качество регулирования выходной переменной. При насыщении координаты управления или некоторой фазовой переменной, применяют нелинейные, например, параболические регуляторы с искусственно введенными ограничениями на коэффициент передачи для исключения образования предельных циклов вблизи установившихся состояний [1, 2]. Однако такой подход не позволяет в полной мере реализовать предельное быстродействие отработки заданных приращений выходной переменной.
Постановка задачи. Как известно [1, 2, 5], ограничение координат состояния электропривода (напряжений, токов, электромагнитных моментов, скорости вращения вала и др.) приводит к нелинейности математической модели ЭМСУ, однако большинство методов синтеза оптимального управления, в том числе по критерию быстродействия, ориентировано на линейные модели объектов управления.
Предлагаемый подход к построению ЭМСУ предельного быстродействия базируется на применении адаптивных к параметрам внешней среды эталонных моделей на входе замкнутых ЭМСУ, обеспечивающих формирование оптимальных по быстродействию изменений именно фазовых переменных [6–10]. К параметрам внешней среды будем относить, прежде всего, заведомо неизвестное во времени изменение положения 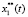 рабочего органа, определяемое датчиками системы локации, технического зрения или иными внешними подсистемами, в том числе с участием оператора. Поскольку внешняя среда может накладывать ограничения на энергетические ресурсы ЭМСУ, то к параметрам внешней среды целесообразно отнести и ограничения на энергию управления. Проще всего это реализовать введением ограничения самой величины управления Um или старшей фазовой переменной.
рабочего органа, определяемое датчиками системы локации, технического зрения или иными внешними подсистемами, в том числе с участием оператора. Поскольку внешняя среда может накладывать ограничения на энергетические ресурсы ЭМСУ, то к параметрам внешней среды целесообразно отнести и ограничения на энергию управления. Проще всего это реализовать введением ограничения самой величины управления Um или старшей фазовой переменной.
Основная часть. На рис. 1 приведена обобщенная функциональная схема ЭМСУ, на которой приняты следующие обозначения: АЭМ – адаптивная эталонная модель, адаптер – устройство, обеспечивающее адаптацию АЭМ к параметрам внешней среды за счет формирования переменного такта управления Ti, ЭМСУ – электромеханическая система управления.

Рис. 1. Функциональная схема ЭМСУ

Рис. 2. Схема имитационного моделирования ЭМСУ с АЭМ

Рис. 3. Схема модели ЭМСУ
В основе решения задачи синтеза оптимального по быстродействию управления ЭМСУ с АЭМ лежат следующие положения.
АЭМ представляет собой замкнутую по вектору состояния дискретно-непрерывную систему финитного управления [1, 2, 6–8]. При этом в качестве объекта управления в самой АЭМ выступает интегратор первого-четвертого порядка, что, по сути, отражает интегро-дифференцирующие связи до четырех заданных фазовых переменных инвариантной ЭМСУ – положения φ*(t), скорости ω*(t), ускорения ε*(t) и рывка ρ*(t).
Векторы фазовых переменных ЭМСУ и АЭМ (рис. 1) в общем случае могут быть представлены в виде:
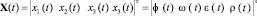 ,
,
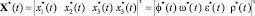 .
.
Поскольку состояние внешней среды априори неизвестно, будем полагать, что начальные значения всех фазовых переменных АЭМ при синтезе могут быть приняты нулевыми:
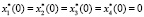 .
.
Тогда период Ti дискретного управления в АЭМ может быть представлен нелинейной функцией приращения задающего воздействия 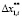 в некоторые дискретные моменты времени (i = 0, 1, 2,…) и предельно допустимого управления Um, т.е. параметров внешней среды.
в некоторые дискретные моменты времени (i = 0, 1, 2,…) и предельно допустимого управления Um, т.е. параметров внешней среды.
Для принятого порядка АЭМ анализ соотношений относительных изменений фазовых переменных в переходных процессах позволяет получить значения переменного периода управления в дискретные моменты времени изменения задающего воздействия:
– n = 1: 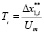 ; (1)
; (1)
– n = 2: 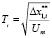 ; (2)
; (2)
– n = 3: 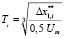 ; (3)
; (3)
– n = 4: 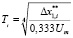 . (4)
. (4)
При условии, что максимальное управление численно равно максимальному значению старшей фазовой переменной, рассчитанные по выражениям (1) – (4) периоды дискретного управления гарантированно обеспечивают ограничение наиболее быстрой старшей фазовой переменной на допустимом уровне.
Критерий качества, лежащий в основе синтеза замкнутой АЭМ, представляет собой предельное быстродействие в концепции цифровых финитных систем управления:
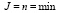 , (5)
, (5)
где n – число тактов дискретного управления, равное числу интеграторов АЭМ; соответственно оптимальное конечное время отработки приращения задающего воздействия составит именно n периодов управления, причем длительность периодов управления в соответствии с (1) – (4) является варьируемой.
Дискретное финитное управление состоянием АЭМ в соответствии с (1) – (5) является нелинейной функцией переменного периода Ti:
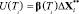 , (6)
, (6)
где 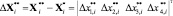 – вектор ошибок отработки приращений фазовых переменных АЭМ в i-й дискретный момент времени; β(Ti) – матрица-строка переменных коэффициентов, являющаяся результатом синтеза оптимального по критерию (5) управления, процедура синтеза которого подробно изложена в [8, 9].
– вектор ошибок отработки приращений фазовых переменных АЭМ в i-й дискретный момент времени; β(Ti) – матрица-строка переменных коэффициентов, являющаяся результатом синтеза оптимального по критерию (5) управления, процедура синтеза которого подробно изложена в [8, 9].
Ниже представлены результаты синтеза для АЭМ первого-четвертого порядка:
– n = 1: 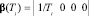 ; (7)
; (7)
– n = 2: 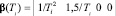 ; (8)
; (8)
– n = 3: 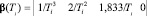 ; (9)
; (9)
– n = 4: 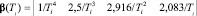 . (10)
. (10)
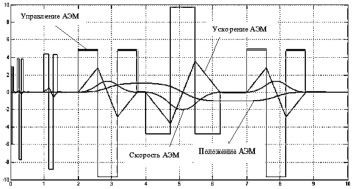
Рис. 4. Результаты моделирования процессов в АЭМ
Инвариантная по отношению к задающему воздействию ЭМСУ отрабатывает эталонные задающие воздействия X*(t) фазовых переменных. В общем случае – это заданное положение φ*(t) рабочего органа и его три производных по времени – скорость, ускорение, рывок. Форма представления сигналов определяется формой сигналов задающих воздействий самой ЭМСУ и параметрами линии связи АЭМ и ЭМСУ. Это могут быть аналоговые, цифровые или широтно-импульсные сигналы.
На рис. 2 приведена схема имитационного моделирования ЭМСУ с АЭМ в интегрированной программной среде MexBIOS Development Studio. При моделировании принято: выходная координата ЭМСУ – положение (рад), порядок АЭМ n = 3; минимальный период управления, определяющий зону линейности модели АЭМ Tmin = 0,005 c; уровень ограничения дискретного регулятора состояния АЭМ и рывка электропривода Um = 10 рад/c3.
Обозначения модулей-подпрограмм на схеме: TestSignal – модуль формирования задающих воздействий, где приняты дискретные моменты времени изменения задающих воздействий (с): t0 = 0, t1 = 0,2, t2 = 1,0, t3 = 2, t4 = 4, t5 = 7 и ступенчатые приращения задающего воздействия (положения ЭМСУ, рад): 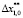 = 0,0001,
= 0,0001, 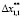 = 0,0009,
= 0,0009, 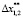 = 0,009,
= 0,009, 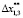 = 0,99,
= 0,99, 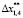 = – 2,0,
= – 2,0, 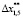 = 1; SolverTvar – модуль вычисления переменного периода управления АЭМ в соответствии с выражением (3); EM Object – объект управления АЭМ, представляющий собой идеальный интегратор 3-го порядка; EM Regulator – регулятор АЭМ, представляющий собой дискретный регулятор состояния с переменным периодом управления, формирующий оптимальное управление АЭМ в соответствии с формулами (6), (9); EMCS – квазиинвариантная по заданию электромеханическая система управления электроприводом постоянного тока, представленная, например, в виде оптимальной по быстродействию замкнутой по состоянию непрерывной системы управлением (рис. 3); StepLoad– модуль формирования ступенчатой нагрузки на валу электропривода. Принято, что нагрузка соответствует статическому току двигателя 2,5 А, время ступенчатого приложения нагрузки – 9,5 с.
= 1; SolverTvar – модуль вычисления переменного периода управления АЭМ в соответствии с выражением (3); EM Object – объект управления АЭМ, представляющий собой идеальный интегратор 3-го порядка; EM Regulator – регулятор АЭМ, представляющий собой дискретный регулятор состояния с переменным периодом управления, формирующий оптимальное управление АЭМ в соответствии с формулами (6), (9); EMCS – квазиинвариантная по заданию электромеханическая система управления электроприводом постоянного тока, представленная, например, в виде оптимальной по быстродействию замкнутой по состоянию непрерывной системы управлением (рис. 3); StepLoad– модуль формирования ступенчатой нагрузки на валу электропривода. Принято, что нагрузка соответствует статическому току двигателя 2,5 А, время ступенчатого приложения нагрузки – 9,5 с.
Обозначения приведенные на схеме: Int1, Int2 – идеальные интеграторы, моделирующие соответственно интегро-дифференцирующие связи между положением и скоростью, скоростью и ускорением (динамическим моментом); TransferFcn – инерционное звено 1-го порядка, аппроксимирующее замкнутый контур регулирования тока якоря (электромагнитного момента); Saturation– звено динамического ограничения, позволяющее ограничить ток якоря на допустимом уровне с возможностью внешнего управления уровнем ограничения; Gain1 – Gain5 – масштабирующие звенья, моделирующие параметры регулятора состояния и полученные в соответствии с методикой, изложенной в [8, 9].
На рис. 4 приведены результаты моделирования процессов в АЭМ, на рис. 5 – в ЭМСУ. Обозначения графиков переменных приведены непосредственно на рисунках, по осям абсцисс – время (с), по осям ординат – абсолютные значения моделируемых переменных.
Анализ результатов моделирования позволяет сделать следующие выводы:
– АЭМ формирует оптимальные по быстродействию задания фазовых переменных, причем ограничение рывка ЭМСУ на уровне 10 рад/с3 происходит только при достаточно больших приращениях задания, сформированных внешней средой, в частности, на 2-й, 4-й и 7-й секундах (рис. 4);
– ЭМСУ отрабатывает эталонное задание фазовых переменных с минимальной инерцией, практически дублируя задание и обеспечивая тем самым предельное быстродействие системы (рис. 5).

Рис. 5. Результаты моделирования процессов в ЭМСУ
Заключение
В результате проведенных исследований предложен новый подход к построению предельных по быстродействию электромеханических систем управления с адаптивными к параметрам внешней среды эталонными моделями. На основе предложенного подхода разработана оригинальная методика синтеза эталонных моделей, обеспечивающих формирование переменного такта дискретного управления и оптимальность формирования до четырех фазовых переменных ЭМСУ по критерию быстродействия. При этом реализуется возможность ограничения на допустимом уровне старшей фазовой переменной и, соответственно, энергии управления. Результаты имитационного моделирования подтвердили эффективность предложенного подхода.
Рецензенты:
Бочкарев С.В., д.т.н., доцент, профессор кафедры микропроцессорных средств автоматизации, ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь;
Цаплин А.И., д.т.н., профессор, зав. кафедрой общей физики, ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.



