Двухуровневое принятие решений представляет собой проблему, в которой два лица, принимающих решения (ЛПР), принимают решения последовательно, один за другим. При этом принятие решений обоими ЛПР происходит на двух разных уровнях иерархии. Каждый ЛПР работает в одном и том же пространстве решений, но с различными и, возможно, конфликтующими целями. При таком подходе ЛПР нижнего уровня принимает решение, после того как принял решение ЛПР верхнего уровня. Несмотря на то, что ЛПР верхнего уровня принимает решение независимо, тем не менее на его решение может повлиять ЛПР нижнего уровня.
Идея двухуровневого принятия решений заключается в следующем: ЛПР верхнего уровня определяет цели и принимает решение, после этого он запрашивает решение от ЛПР нижнего уровня, полученное независимо, в соответствии с целями последнего. Получив решение от ЛПР нижнего уровня, ЛПР верхнего уровня рассматривает его и изменяет в соответствии с целями двухуровневого принятия решений. Затем ЛПР нижнего уровня опять принимает решение уже с учетом этого нового решения ЛПР верхнего уровня. Процесс продолжается до тех пор, пока не будет получено удовлетворяющее решение [14].
ЛПР верхнего уровня, лидер, принимает стратегические решения. ЛПР нижнего уровня, ведомый, принимает решения в установленных рамках. Например, в качестве лидера может выступать правительство, которое намерено сократить воздействие на окружающую среду и обеспечить финансовый баланс в области энергосбережения, а также уменьшить выбросы углерода. Предприятие, выступающее в роли ведомого, стремится оптимизировать свои расходы в условиях субсидирования и штрафов, определяемых правительством [13].
Двухуровневое принятие решений находит широкое применение при решении различных практических задач в технических, экономических и организационных системах. Так, в работе [6] описана двухуровневая система поддержки принятия решений, предназначенная для проектирования дорожно-транспортной сети. Предложена двухуровневая модель принятия решений, целью которой является уменьшение задержки в пути участников дорожного движения и, одновременно с этим, снижение уязвимости сети. В статье [10] разработана новая модель принятия решений, использующая двухуровневое программирование, предназначенная для планирования строительного проекта в нечеткой случайной среде с ограниченными ресурсами. Инвестор, который выступает в качестве ЛПР верхнего уровня, стремится к максимизации прибыли, тогда как подрядчик, как ЛПР нижнего уровня, пытается минимизировать затраты. Эффективность предложенной модели подтверждена при строительстве ГЭС в г. Nuozhadu, Китай. В статье [8] представлен метод формализации процесса изготовления бумаги и выполняемых при этом технологических операций. Этот метод основывается на двухуровневом принятии решений и позволяет избежать излишних итераций во время процесса изготовления бумаги. В статье [12] представлена двухуровневая система, где задача оптимизации решается на основе целочисленного линейного программирования на верхнем уровне системы, реакция на предложенное решение происходит на нижнем уровне. Разработанная система предлагается к использованию при управлении гибкими производственными системами. В статье [15] предложена модель двухуровневого программирования, предназначенная для выбора места размещения нефтедобывающей платформы с учетом ограниченных ресурсов и стохастического характера изменения цен на нефть. На верхнем уровне модели принятие решений происходит на основе адаптивного алгоритма оптимизации, алгоритм поиска с запретами используется на нижнем уровне принятия решений и обеспечивает верификацию решения верхнего уровня. В работе [9] предложен новый подход к выбору пути беспилотных летательных аппаратов в реальном времени на основе двухуровневого программирования. Проблема выбора оптимального пути формализована как модель лидер – ведомый. Данный подход позволяет найти оптимальный путь с учетом всех возможных путей достижения цели, обхода препятствий, длины различных путей, сглаживания траектории полета и адаптации к изменениям кинематических и сенсорных свойств беспилотного летательного аппарата.
Область применения двухуровневого программирования не ограничивается указанными выше примерами, что подтверждает важность и актуальность проблемы создания методов и средств, предназначенных для повышения эффективности двухуровневого принятия решений.
Формальное представление проблемы двухуровневого принятия решений
Пусть вектор переменных решения х = (x1, x2) ∈ Rn определяется лицами, принимающими решения, двух уровней: ЛПР верхнего уровня и ЛПР нижнего уровня. Тогда ЛПР верхнего уровня может управлять вектором x1 ∈ Rn1, в то время как ЛПР нижнего уровня может управлять вектором x2 ∈ Rn2, где n = n1 + n2. Кроме того, предположим, что
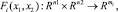i = 1, 2
являются векторами нелинейных целевых функций верхнего и нижнего уровней соответственно.
Проблема двухуровневого принятия решений может быть сформулирована следующим образом: решение может быть получено в том случае, если для верхнего уровня достигнута цель:
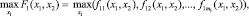
в то время как для x2
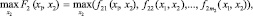
при условии
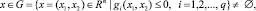
где х1 = (x11, x12, …, x1n1), х2 = (x21, x22, …, x2n2); G – множество ограничений; mi, i = 1, 2 – количество целевых функций i-го ЛПР; q – количество ограничений.
На верхнем и нижнем уровнях могут быть использованы различные методы и алгоритмы принятия решений. В данной статье при принятии решений предлагается использовать методы, отлично зарекомендовавшие себя в задачах традиционного одноуровневого принятия решений, которые основаны на близости альтернатив к идеальной альтернативе.
Определение альтернативы, ближайшей к идеальной альтернативе
На сегодняшний день разработан ряд методов принятия решений с учетом близости к идеальной альтернативе или идеальной точке, в основе которых лежит понятие меры расстояния [1–5, 7, 11]. Идеальная альтернатива, как правило, вводится искусственно на основе лучших значений целевых функций. Выбор лучшей альтернативы из множества рассматриваемых происходит при решении задачи минимизации расстояния от текущей альтернативы до идеальной. При этом некоторые методы, в частности метод упорядоченного предпочтения через сходство с идеальным решением, учитывают не только близость к идеальной наилучшей альтернативе, но и удаленность от идеальной наихудшей альтернативы [4].
Рассмотрим вектор целевых функций F(х) = (f1(х), f2(х), …, fm(х)) в m-целевом пространстве. Тогда идеальной альтернативе будет соответствовать вектор
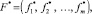
где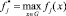 
, j = 1, 2, …, m. Для идеальной наихудшей альтернативы в этом случае можно определить вектор
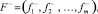
где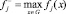 
, j = 1, 2, …, m. В качестве меры близости может использоваться Lp-метрика, которая определяет расстояние между двумя точками F(х) и F*:
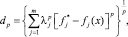p = 1, 2, ..., ∞,
где lj, j = 1, …, m – относительная важность (вес) цели.
Если целевые функции fj(х), j = 1, …, m, несоизмеримы, то необходимо их нормализовать: функции масштабируются и представляются в безразмерном виде на интервале [0, 1]. Для этого может быть использована следующая метрика:
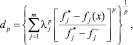p = 1, 2, ..., ∞.
Задачу выбора альтернативы, ближайшей к идеальной, можно записать в следующем виде:
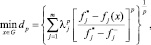
p = 1, 2, ..., ∞.
Выбор значения параметра p отражает способ обеспечения компромисса между целями. Параметр р определяет баланс между общей полезностью и максимальной индивидуальной уступкой. С увеличением значения р общая полезность (расстояние dp) уменьшается, т.е. d1 ≥ d2 ≥ … ≥ dp и наибольшее внимание уделяется наибольшему отклонению при определении конечного результата. Так, p = 1 подразумевает равную важность (вес) для всех отклонений. При p = 2 веса отклонений пропорциональны величине отклонений. Наконец, для p = ∞ наибольшее отклонение полностью доминирует при определении расстояния, а L∞-метрика имеет вид
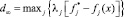
или
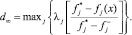
Заключение
Двухуровневое принятие решений представляет собой процесс взаимосвязанного принятия решений лицами, принимающими решения, верхнего и нижнего уровней с целью получения оптимального результата, основываясь на компромиссе при достижении целей ЛПР обоих уровней иерархии. Проведенный анализ литературных источников показал необходимость и актуальность разработки новых методов и подходов, позволяющих повысить эффективность решения задачи двухуровневого принятия решений. В статье представлена формализация данной проблемы при принятии решений на двух уровнях иерархии. Принятие решений на каждом из уровней может выполняться с применением существующих методов и алгоритмов с учетом особенностей проблемной области. В данной работе предложена концепция двухуровневого принятия решений на основе близости к идеальной альтернативе, что позволяет использовать широко известные методы принятия решений, основанные на близости рассматриваемых альтернатив к идеальной альтернативе, которые уже подтвердили свою эффективность при решении различных практических задач.
Рецензенты:
Бронов С.А., д.т.н., профессор, руководитель научно-учебной лаборатории систем автоматизированного проектирования кафедры систем искусственного интеллекта, Сибирский федеральный университет, г. Красноярск.
Ченцов С.В., д.т.н., профессор, зав. кафедрой «Системы автоматики, автоматизированное управление и проектирование», Сибирский федеральный университет, г. Красноярск.