В настоящее время существуют несколько различных способов эхокомпенсации, отличающиеся сложностью реализации, точностью компенсации и т.п. Одним из способов является инвариантная эхокомпенсация, подкупающая своей простотой реализации. Однако она мало изучена, поэтому представляет научный и практический интерес оценка количественных характеристик и параметров, что и проделано в данной работе.
В реальных условиях работы инвариантного эхокомпенсатора следует учитывать воздействие на режим его функционирования множества факторов: изменения температуры, изменения параметров используемого канала связи и т.д. Очевидно, что в результате этих неконтролируемых изменений будет происходить варьирование параметров эхотрактов.
Оценим, каким образом это повлияет на качество работы инвариантного эхокомпенсатора, а именно на величину погрешности компенсации эха.
Для этого рассмотрим преобразования отсчетов сигналов в упрощенной схеме инвариантного эхокомпенсатора (рис. 1).
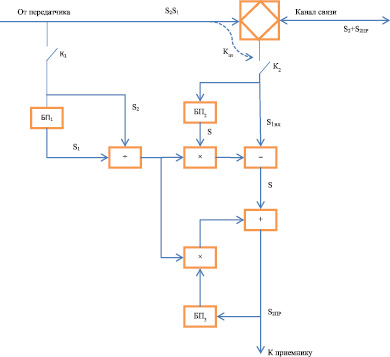
Рис. 1. Упрощенная схема инвариантного эхокомпенсатора
В этой схеме компенсация эха осуществляется путем обработки временных отсчетов сигналов, которые формируются ключами К1 и К2.
В блоках памяти БП1, БП2 и БП3 осуществляется хранение временных отчетов в течение времени, равного интервалу дискретизации. Эта упрощенная схема работает следующим образом.
Перед сеансом связи схема подвергается обучению. С этой целью передатчик передает обучающий короткий импульс SОБ, который проходит через паразитный эхотракт дифференциальной системы и записывается в блок памяти БП2 в виде импульса
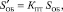
где Кпт – коэффициент ослабления импульсов паразитного эхотракта. Блок памяти БП3 в это время обнулен. Облучающий импульс через ключ К1 поступает также в блок памяти БП1. Затем начинается рабочий режим.
Рассмотрим передачу двух следующих друг за другом временных отсчетов S1 и S2 передаваемого сигнала. Первый отсчет будет передан в канал, кроме того, он пройдет через паразитный эхотракт и поступит на вход вычитателя вместе с отчетом S1пр сигнала, принимаемого от противоположной стороны. Таким образом, на верхний вход вычитателя поступит следующая сумма:
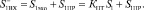(1)
На второй вход вычитателя придет сигнал
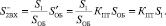(2)
На выходе вычитателя появится следующий результат:
(3)
Как видно из результата, на данном этапе имеет место полное подавление эха.
Продолжим анализ работы схемы на втором этапе, когда от передатчика поступает второй отсчет S2.
В конце первого такта величина S1ЭХО + S1ПР = КПТS1 + S1ПР была записана в блок памяти БП2, S1ПР – в БП3, а S1 – в БП1. На втором такте на первый вход вычитателя поступит сумма
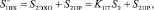(4)
на второй вход
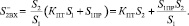(5)
На выходе вычитателя имеем
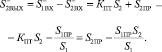(6)
На выход сумматора результат равен
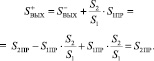(7)
Как показывает расчет и на втором такте, эхо на выходе сумматора эхокомпенсатора (на входе приемника) по-прежнему отсутствует.
Нетрудно убедиться в том, что это будет справедливо и для всех последующих тактов работы.
Однако это верно до тех пор, пока не изменятся параметры эхотракта, например вследствие изменения параметров подключенного к дифференциальной системе канала связи.
Проанализируем последствия изменения коэффициентов ослабления паразитного эхотракта на величину ∆КПТ, которое может произойти из-за изменений параметров канала связи во время рабочего режима.
Предположим, что это произошло на j-м такте работы эхокомпенсатора. При этом на выходе вычитателя появится погрешность компенсации эха:
(8)
Эта погрешность поступает в нижний контур и начинает в ней циркулировать, ответвляясь при этом на вход приемника. Через n тактов после изменения параметров канала величина погрешности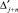 
во втором контуре будет равна
(9)
Таким образом, возникновение неустраняющейся погрешности эхокомпенсации вследствие изменения параметров эхотракта говорит об отсутствии у инвариантных эхокомпенсаторов свойства адаптивности, что ограничивает возможность их использования в каналах связи с существенными изменениями параметров во время сеанса связи.
Исходя из этого, можно сделать вывод о том, что адаптация инвариантного эхокомпенсатора возможна, если применить новую адаптивную структурную схему инвариантного эхокомпенсатора которая представлена на рис. 2.
Для анализа и получения результатов экспериментального исследования адаптивного инвариантного эхокомпенсатора была разработана моделирующая программа, написанная в среде Matlab, для имитации процессов, происходящих при обучении и дальнейшей работе предложенной схемы адаптивного инвариантного эхокомпенсатора.
Качество работы предложенной схемы оценивается величиной среднего квадратичного отклонения (СКО) при разных уровнях шума.
Были рассмотрены три варианта организации работы схемы эхокомпенсатора при введении помехи в виде белого шума. В первом случае эхокомпенсатор без преобразований, то есть только при наличии дифференциальной системы с изменяющимися параметрами; во втором – эхокомпенсатор плюс схема адаптации и схема вычитания передаваемого сигнала; в третьем – эхокомпенсатор и схема адаптации. Для наглядного сравнения также показаны изменения помехи в виде белого шума.
В качестве исследуемого сигнала был взят синусоидальный сигнал как основной, однако для сравнения был исследован при таких же условиях сигнал прямоугольной формы.
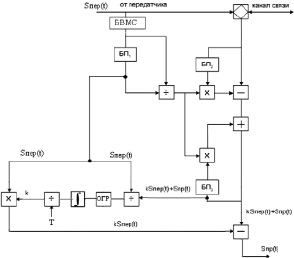
Рис. 2. Схема адаптивного инвариантного эхокомпенсатора
Зависимость СКО от количества испытаний при синусоидальной форме сигнала
|
n |
30 |
50 |
100 |
500 |
1000 |
5000 |
10000 |
50000 |
|
vv |
0,5988 |
2,0124 |
0,8778 |
2,1196 |
2,276 |
2,1224 |
2,1318 |
2,1463 |
|
vv1 |
2,2587 |
0,6828 |
0,7797 |
3,7203 |
4,4549 |
4,2234 |
4,3432 |
4,2189 |
|
vv2 |
0,3356 |
0,3264 |
0,3109 |
0,3601 |
0,3617 |
0,3547 |
0,3562 |
0,3563 |
|
vv3 |
3,251 |
3,325 |
2,4185 |
0,5894 |
0,3625 |
0,356 |
0,3803 |
0,3577 |
|
y |
20,6126 |
21,8382 |
22,7966 |
21,9027 |
21,561 |
21,6537 |
21,6685 |
21,7108 |
Используемые обозначения:
vv – эхокомпенсатор без преобразований;
vv1 – эхокомпенсатор, схема адаптации и вычитание передаваемого сигнала;
vv2 – помеха в виде белого шума;
vv3 – эхокомпенсатор, схема адаптации;
y – уровень вводимого шума, дБ;
n – количество испытаний.
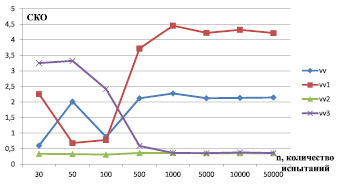
Рис. 3. График зависимости СКО от количества испытаний при синусоидальном сигнале
Результаты исследования влияния помехи в виде белого шума на качество эхокомпенсации при различных вариантах организации работы схемы представлены в таблице, а графики исследования показаны на рис. 3.
Рассмотрим зависимость СКО от количества проведенных испытаний.
Для синусоидального сигнала: при коэффициенте рассогласования дифференциальной системы, равном 0,5, и дисперсии белого шума, равной 0,1.
Полученные результаты, показывающие зависимость средней квадратичной ошибки (СКО) от дисперсии белого шума при различных формах сигналов, подтверждают предыдущие показания, то есть доказывают, что предложенная схема адаптивного инвариантного эхокомпенсатора является работоспособной в условиях действия помехи в виде белого шума.
Рецензенты:
Пальчун Ю.А., д.т.н., профессор, ученый секретарь, Сибирский государственный ордена Трудового Красного знамени научно-исследовательский институт метрологии, г. Новосибирск;
Сединин В.И., д.т.н., профессор, заведующий кафедрой «Системы автоматизированного проектирования», ФГБОУ ВПО «Сибирский государственный университет телекоммуникаций и информатики», г. Новосибирск.