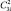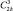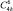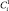Ранее, в работах [1, 2] и ряде других публикаций одного из авторов данной работы была построена общая феноменологическая теория магнитных фазовых переходов (ФП) в 3d-элементах и их магнитных соединениях. Было показано, что в этих кристаллах магнитная анизотропия возникает не в точке Кюри – Нееля (при Т = Тc), а при более низкой температуре Т = Тls, так, что в интервале Tls < Т < Tc существует магнитная фаза без анизотропии, свойства которой обусловлены только обменными взаимодействиями. В простейшем случае ферромагнетика намагниченность можно представить в виде суммы двух слагаемых 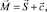 где
где 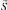 – спиновая (обменная) часть,
– спиновая (обменная) часть,  – вклад в намагниченность, обусловленный релятивистскими взаимодействиями. В парамагнитной фазе оба этих слагаемых равны нулю, а ниже точки Кюри возникает чисто спиновая часть
– вклад в намагниченность, обусловленный релятивистскими взаимодействиями. В парамагнитной фазе оба этих слагаемых равны нулю, а ниже точки Кюри возникает чисто спиновая часть 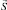 , причем вектор
, причем вектор 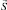 является критическим параметром порядка (ПП) для перехода в точке Кюри. Вклад релятивистских взаимодействий в намагниченность
является критическим параметром порядка (ПП) для перехода в точке Кюри. Вклад релятивистских взаимодействий в намагниченность  возникает в точке перехода в анизотропную фазу Tls, а вектор
возникает в точке перехода в анизотропную фазу Tls, а вектор  является критическим ПП для перехода из изотропной фазы в анизотропную. На кривой температурной зависимости намагниченности М(Т) включение орбитального вклада с(Т) ниже температуры Tls должно отобразиться в виде появления на графике «горбика» в окрестности точки T = Tls, если орбитальный вклад направлен по направлению вектора
является критическим ПП для перехода из изотропной фазы в анизотропную. На кривой температурной зависимости намагниченности М(Т) включение орбитального вклада с(Т) ниже температуры Tls должно отобразиться в виде появления на графике «горбика» в окрестности точки T = Tls, если орбитальный вклад направлен по направлению вектора 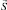 и «впадины», если направление орбитального вклада противоположно. И действительно, для кристалла медного феррита CuFe2O4 – типичного обменного магнетика, на экспериментальной кривой М(Т) при температуре перехода из кубической (изотропной) в тетрагональную (анизотропную) фазу имеется хорошо выраженный «горбик» [12].
и «впадины», если направление орбитального вклада противоположно. И действительно, для кристалла медного феррита CuFe2O4 – типичного обменного магнетика, на экспериментальной кривой М(Т) при температуре перехода из кубической (изотропной) в тетрагональную (анизотропную) фазу имеется хорошо выраженный «горбик» [12].
Предложенная в [1, 2] теория носила чисто феноменологический характер и не учитывала какой-либо специфики того, что при спин-орбитальном переходе происходит упорядочение орбиталей, вызывающее появление орбитальных токов и, как следствие, орбитального магнитного момента, вносящего вклад в намагниченность. В данной работе мы имеем намерение связать орбитальный вклад в намагниченность с квантовомеханическими величинами, описывающими орбитальное упорядочение, и с орбитальными токами. Анализ механизма кооперативного спин-орбитального эффекта рассмотрим на примере кристаллов со структурой шпинели. Весьма показателен в этом отношении феррит титана (ульвошпинель) Fe2TiO4. В точке Кюри – Нееля при Тс = 147 К кристалл ульвошпинели переходит в магнитоупорядоченное состояние – становится Неелевским антиферромагнетиком. При TJT = 115 K кристалл испытывает структурный переход из кубической фазы в тетрагональную, который сопровождается резким увеличением магнитной анизотропии и появлением слабого ферромагнетизма [8]. Принято считать [9, 11] переход при TJT = 115 K ян-теллеровским переходом, обусловленным двухвалентными ионами железа. При T2 = 77 K кристалл испытывает еще один структурный переход из тетрагональной в моноклинную фазу [6]. Катионное распределение в ульвошпинели имеет следующий вид: Fe+2[Fe+2Ti+4]O–24. При таком распределении катионов ян-теллеровскими являются ионы железа и в тетраэдрической, и в октаэдрической подрешетках. При этом катионы Fe+2 в октаэдрической подрешетке имеют трехкратно вырожденные орбитальные состояния, а ионы в тетраэдрической подрешетке являются eg-ионами [10]. Таким образом, в последовательности фазовых переходов, происходящих в ульвошпинели, спиновое и орбитальное упорядочение, а также их взаимовлияние играет самую непосредственную роль. Обратимся к подробному рассмотрению этого вопроса.
Кристаллы со структурой шпинели характеризуются в парамагнитной фазе ОЦК решеткой, симметрия которой описывается пространственной группой 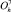 . Симметрия кристаллической решетки сохраняется и в изотропной магнитной фазе и изменяется только ниже точки спин-орбитального фазового перехода. Переход из изотропной в анизотропную ферромагнитную фазу описывается трехмерным ПП
. Симметрия кристаллической решетки сохраняется и в изотропной магнитной фазе и изменяется только ниже точки спин-орбитального фазового перехода. Переход из изотропной в анизотропную ферромагнитную фазу описывается трехмерным ПП 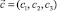 [1], который преобразуется по неприводимому представлению (НП) F1g группы симметрии кристалла
[1], который преобразуется по неприводимому представлению (НП) F1g группы симметрии кристалла 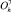 . Для корректного описания ФП, связанных с изменением квантовых орбитальных состояний 3d-электронов, ПП должен быть выражен через элементы матрицы плотности [3].
. Для корректного описания ФП, связанных с изменением квантовых орбитальных состояний 3d-электронов, ПП должен быть выражен через элементы матрицы плотности [3].
Состояния ян-телллеровского (ЯТ-)иона, находящегося в постоянном взаимодействии с кристаллом, по общим правилам квантовой механики должны описываться с помощью матрицы плотности, оператор которой в собственном базисе имеет вид [3, 6]
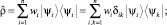
ρik = wiδik 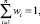 (1)
(1)
где δik – символ Кронеккера; 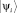 – собственные векторы
– собственные векторы  ; wi – вероятности пребывания ЯТ-иона в состояниях
; wi – вероятности пребывания ЯТ-иона в состояниях 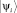 ; ρik = wiδik – матричные элементы. В исходной фазе вероятности заселенностей wi всех n состояний одинаковы: wi = 1/n, поэтому
; ρik = wiδik – матричные элементы. В исходной фазе вероятности заселенностей wi всех n состояний одинаковы: wi = 1/n, поэтому 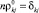 , т.е. в исходной фазе матрица плотности пропорциональна единичной. Поэтому в низкосимметричной фазе
, т.е. в исходной фазе матрица плотности пропорциональна единичной. Поэтому в низкосимметричной фазе  можно записать так:
можно записать так:
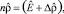 (2)
(2)
где 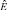 – единичная n×n-матрица, а второе слагаемое
– единичная n×n-матрица, а второе слагаемое 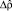 – бесследная часть оператора
– бесследная часть оператора  , возникающая ниже точки ФП, причем
, возникающая ниже точки ФП, причем 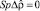 . Величина
. Величина 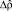 , согласно (2) описывает появление новых свойств в низкосимметричной фазе. Для любой бесследной эрмитовой n×n-матрицы существует линейно-независимый набор бесследных n×n-матриц
, согласно (2) описывает появление новых свойств в низкосимметричной фазе. Для любой бесследной эрмитовой n×n-матрицы существует линейно-независимый набор бесследных n×n-матриц 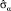 , по которым ее можно разложить [3, 6]:
, по которым ее можно разложить [3, 6]:
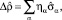 (3)
(3)
где 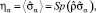
где α – номер НП, входящего в тензорное (ян-теллеровское) представление, реализующееся на Δρik. Размерность s легко вычислить. В общем случае комплексная n×n-матрица зависит от 2n2 произвольных действительных параметров. Условие равенства нулю следа матрицы и n2 условий эрмитовости дают s = 2n2 – n2 – 1 = n2 – 1. Следовательно, многомерный ПП  , описывающий снятие вырождения и упорядочение T2g-орбиталей, имеет 8 компонент. Так как у кубической группы Oh нет НП с размерностями больше 3-х,
, описывающий снятие вырождения и упорядочение T2g-орбиталей, имеет 8 компонент. Так как у кубической группы Oh нет НП с размерностями больше 3-х,  преобразуется по приводимому представлению и из его компонент можно выделить неприводимые составляющие. Ниже мы приведем результат такого анализа.
преобразуется по приводимому представлению и из его компонент можно выделить неприводимые составляющие. Ниже мы приведем результат такого анализа.
Нам необходимо связать ηα с вероятностями занятия орбитальных состояний wi. Для этого следует в (1) перейти от собственного базиса 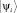 к произвольному ортонормированному базису
к произвольному ортонормированному базису 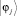 с помощью некоторого унитарного преобразования
с помощью некоторого унитарного преобразования 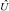 :
: 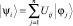 . Тогда матричные элементы оператора
. Тогда матричные элементы оператора  будут выражены через вероятности wi и матричные элементы унитарного оператора
будут выражены через вероятности wi и матричные элементы унитарного оператора 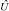
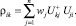 (4)
(4)
Выразим матрицу  , по формулам (2), (3) задавая явный вид базисных матриц
, по формулам (2), (3) задавая явный вид базисных матриц 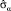 . В качестве базисных 3×3 матриц
. В качестве базисных 3×3 матриц 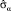 [3, 6]:
[3, 6]:
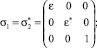
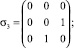
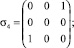
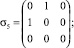 (5)
(5)
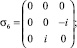
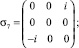
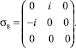
Как следствие, получаем следующие уравнения связи ηα с wi и Uij:
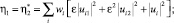
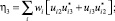
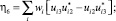 (6)
(6)
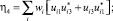
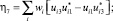
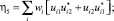
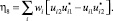
В качестве базисных электронных волновых функций трехкратно вырожденного Т2g-уровня обычно выбирают набор вещественных волновых функций φ1, φ2, φ3, определяемых соотношениями
r2φ1 = yz; r2φ2 = zx; r2φ3 = xy. (7)
Итак, мы имеем восемь компонент приводимого ПП  . Какие из них соответствуют ферромагнитному переходу по НП F1g? Для ответа на этот вопрос надо разложить приводимое представление Γ(η) по НП группы Oh. Используя метод приводящей матрицы в применении к образам генераторов группы Oh и приведя их к блочно-диагональной форме, мы получили следующее разложение исходного представления на два трехмерных и двукратное одномерное
. Какие из них соответствуют ферромагнитному переходу по НП F1g? Для ответа на этот вопрос надо разложить приводимое представление Γ(η) по НП группы Oh. Используя метод приводящей матрицы в применении к образам генераторов группы Oh и приведя их к блочно-диагональной форме, мы получили следующее разложение исходного представления на два трехмерных и двукратное одномерное
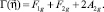 (8)
(8)
Как показал наш анализ, по псевдовекторному НП F1g преобразуется трехкомпонентный вектор 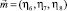 . По НП F2g преобразуется еще один трехкомпонентный вектор
. По НП F2g преобразуется еще один трехкомпонентный вектор 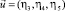 . Наконец, две компоненты η1 и η2 восьмимерного ПП
. Наконец, две компоненты η1 и η2 восьмимерного ПП  преобразуются независимо друг от друга – по одному и тому же одномерному НП A2g. Физическая роль НП, входящих в правую часть разложения (8), совершенно различна. ПП
преобразуются независимо друг от друга – по одному и тому же одномерному НП A2g. Физическая роль НП, входящих в правую часть разложения (8), совершенно различна. ПП 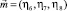 , преобразующийся по НП F1g, определяет всю физику фазового перехода в ближайшей окрестности точки спин-орбитального перехода T = Tls – изменение симметрии кристалла, температурные зависимости основных термодинамических величин. Это критический параметр порядка, и, соответственно, F1g – критическое НП. Остальные НП в правой части (8) описывают сопутствующие фазовому переходу явления – эти НП называются некритическими, а им соответствуют вторичные ПП. Для каждого возможного критического НП можно вычислить сопутствующие ему НП – и этот набор – критическое НП и совокупность некритических НП – образует так называемый полный конденсат [5]. В полный конденсат критического НП F1g, кроме указанных в (8), входят еще двумерное НП Eg и единичное НП A1g. Термодинамика ФП с критическим НП F1g была подробно рассмотрена [1–2], и специфика орбитального упорядочения не привносит в нее ничего нового. Новой является физическая интерпретация явлений, описываемых вторичными параметрами порядка, соответствующим НП F2g и A2g.
, преобразующийся по НП F1g, определяет всю физику фазового перехода в ближайшей окрестности точки спин-орбитального перехода T = Tls – изменение симметрии кристалла, температурные зависимости основных термодинамических величин. Это критический параметр порядка, и, соответственно, F1g – критическое НП. Остальные НП в правой части (8) описывают сопутствующие фазовому переходу явления – эти НП называются некритическими, а им соответствуют вторичные ПП. Для каждого возможного критического НП можно вычислить сопутствующие ему НП – и этот набор – критическое НП и совокупность некритических НП – образует так называемый полный конденсат [5]. В полный конденсат критического НП F1g, кроме указанных в (8), входят еще двумерное НП Eg и единичное НП A1g. Термодинамика ФП с критическим НП F1g была подробно рассмотрена [1–2], и специфика орбитального упорядочения не привносит в нее ничего нового. Новой является физическая интерпретация явлений, описываемых вторичными параметрами порядка, соответствующим НП F2g и A2g.
Рассмотрим это подробнее. Как было показано в [3], часть компонент ПП  описывает изменение плотности заряда на узле, занятом ЯТ-ионом, а другая часть описывает возникновение узельного тока, и эти два набора не пересекаются. Но, как известно уже из курса общей физики, с замкнутым круговым током связан соответствующий магнитный момент этого тока. Поэтому, спин-орбитальный переход в анизотропную магнитную фазу описывается теми из восьми компонент
описывает изменение плотности заряда на узле, занятом ЯТ-ионом, а другая часть описывает возникновение узельного тока, и эти два набора не пересекаются. Но, как известно уже из курса общей физики, с замкнутым круговым током связан соответствующий магнитный момент этого тока. Поэтому, спин-орбитальный переход в анизотропную магнитную фазу описывается теми из восьми компонент  , которые входят в выражение для плотности узельного тока.
, которые входят в выражение для плотности узельного тока.
Из общей квантовомеханической формулы <А> = Sp(Aρ), примененной к матрице оператора тока
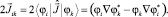 (9)
(9)
Получается следующее выражение для плотности среднего узельного тока [10]:
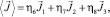 (10)
(10)
а базисные токи имеют вид
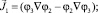
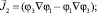
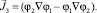 (11)
(11)
Аналогичным образом для матрицы оператора плотности заряда с элементами dik = φiφk получается выражение для среднего значения заряда, на узле, занятом ЯТ-ионом:
 (12)
(12)
Отсюда видно, что в случае действительных волновых функций (7) слагаемые с η6,η7,η8 выпадают из плотности заряда. Конкретная пространственная конфигурация электронного тока на узле определяется координатной зависимостью электронных волновых функций. Так, для тока <J> легко получить, при η6 = η7 = 0, η8 = 1
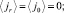
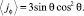 (13)
(13)
Таким образом, спин-орбитальный ФП должен описываться трехмерным ПП 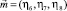 . Этот ПП преобразуется по НП F1g и пропорционален классическому ПП
. Этот ПП преобразуется по НП F1g и пропорционален классическому ПП 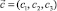 , использованному в работах [1, 2].
, использованному в работах [1, 2].
В работах [1, 2] были найдены магнитоанизотропные фазы (таблица) и проведен термодинамический анализ фазовых превращений, как по критическим степеням свободы, так и по некритическим. Эти результаты остаются в силе и при явном учете орбитальных состояний. Однако теперь мы можем точно вычислить величины орбитальных магнитных моментов и соответствующих им узельных токов для каждой из четырех низкосимметричных фаз, приведенных в таблице. Отметим, что при переходе в тригональную 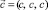 и тетрагональную
и тетрагональную 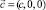 фазы 3-кратное вырождение орбитального состояния может сниматься не полностью. Может оказаться, что основное состояние ниже перехода – это дублет. Тогда снятие этого вырождения произойдет уже при дальнейшем переходе в моноклинную или триклинную фазы.
фазы 3-кратное вырождение орбитального состояния может сниматься не полностью. Может оказаться, что основное состояние ниже перехода – это дублет. Тогда снятие этого вырождения произойдет уже при дальнейшем переходе в моноклинную или триклинную фазы.
Низкосимметричные фазы, индуцированные НП F1g группы 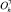
|
|
ccc |
occ |
coo |
c1c2c3 |
|
GD |
|
|
|
|
Данная таблица позволяет получить важную информацию о типах орбитального упорядочения, соответствующих приведенным там низкосимметричным фазам. Модуль параметра порядка 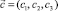 имеет размерность намагниченности, а модуль вектора
имеет размерность намагниченности, а модуль вектора 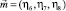 есть величина безразмерная. При этом модуль
есть величина безразмерная. При этом модуль  не превосходит единицы. Поэтому линейная связь между
не превосходит единицы. Поэтому линейная связь между  и
и  должна иметь следующий вид:
должна иметь следующий вид:
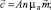
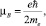 (14)
(14)
где А – константа; n – число примитивных ячеек в единице объема; μB – магнетон Бора. Таким образом, в соответствии с таблицей и соотношением (14) компоненты (η6, η7, η8) восьмимерного ПП  принимают вполне определенные значения и подчиняются определенным правилам пропорций, тогда как остальные компоненты равны нулю. Подставляя эти значения (η6, η7, η8) в систему уравнений (6), мы получаем возможность вычислить зависимость вероятностей реализации wi определенных орбитальных состояний от термодинамических параметров, если была определена предварительно зависимость от этих параметров модуля ПП
принимают вполне определенные значения и подчиняются определенным правилам пропорций, тогда как остальные компоненты равны нулю. Подставляя эти значения (η6, η7, η8) в систему уравнений (6), мы получаем возможность вычислить зависимость вероятностей реализации wi определенных орбитальных состояний от термодинамических параметров, если была определена предварительно зависимость от этих параметров модуля ПП  . Кроме вероятностей, из той же системы определяются матричные элементы унитарного оператора
. Кроме вероятностей, из той же системы определяются матричные элементы унитарного оператора 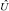 . Это позволяет проследить за изменением спинового и орбитального упорядочений в соответствии с изменением значений термодинамических параметров.
. Это позволяет проследить за изменением спинового и орбитального упорядочений в соответствии с изменением значений термодинамических параметров.
Таким образом, метод локальной матрицы плотности позволяет естественным и непротиворечивым образом объединить методы термодинамики и квантовой механики и построить теорию спин-орбитального фазового перехода и тем самым подтвердить гипотезу Гуденафа [7] и Кугеля – Хомского [4] о существовании таких переходов.
Рецензенты:
Диканский Ю.И., д.ф.-м.н., профессор, заведующий кафедрой общей физики, Северо-Кавказский федеральный университет, г. Ставрополь;
Эдиев Д.М., д.ф.-м.н., профессор кафедры математики, Северо-Кавказская государственная гуманитарно-технологическая академия, г. Черкесск.