Анализируя современные работы по описанию процесса пресечения вирусных атак, можно заметить, что многие авторы используют принципы моделирования распространения эпидемии инфекционных заболеваний [3, 4, 6–11]. Основоположниками данного подхода стали Д.O. Кепхарт и С.Р. Уайт [6].
Рассмотрим n локальных вычислительных сетей (групп), объединенных в одну глобальную сеть. Такая ситуация может возникнуть, если предприятие (или отрасль) занимает обширную территорию. В этом случае локальные сети связывают между собой с помощью любых традиционных каналов связи. Процесс распространения вредоносного кода в j группе, 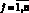 , на промежутке времени [0, Т], описывается с помощью эпидемиологической модели в следующих предположениях [3, 4, 8, 9]:
, на промежутке времени [0, Т], описывается с помощью эпидемиологической модели в следующих предположениях [3, 4, 8, 9]:
1) Nj(t) – общее количество машин в j группе, 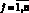 ;
;
2) произвольный узел сети может находиться в трех состояниях: уязвимом Sj(t), инфицированном Ij(t) и невосприимчивом Rj(t);
3) распространение копии вредоносной программы описывается с помощью функции роста fj(t, S(t), I(t), B), 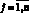 , которая может учитывать характеристики вирусной атаки и самой сети с помощью вектора параметров B = (β1(t), ..., βm(t));
, которая может учитывать характеристики вирусной атаки и самой сети с помощью вектора параметров B = (β1(t), ..., βm(t));
4) вредоносная программа имеет некий латентный период h1(t), во время которого компьютер считается зараженным, но вирус не наносит какого-либо вреда инфицированному узлу;
5) количество компьютеров в сети является переменным числом, и функция b(t) характеризует скорость прироста новых уязвимых узлов;
6) в реальных условиях «лечение» происходит за счет установки антивирусного программного обеспечения или межсетевых экранов. При этом иммунитет приобретают не только инфицированные компьютеры, но и уязвимые со скоростью иммунизации в единицу времени 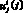 , i = 1, 2,
, i = 1, 2, 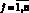 соответственно;
соответственно;
7) с постоянной скоростью μ компьютеры отключаются от сети, при этом отключение не связано с вирусной атакой;
8) на практике антивирусная защита работает для определенного вредоносного ПО. При появлении нового вида вируса узел опять становится уязвимым с частотой заражения σ и с временем задержки h2(t).
В соответствии с этими предположениями получаем следующую систему дифференциальных уравнений с запаздыванием в аргументе
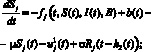 (1)
(1)
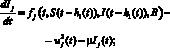 (2)
(2)
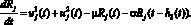 (3)
(3)
Предполагаем, что на начальном множестве E0 = {t ∈ [θ, 0], θ < 0} количество компьютеров разных классов известно:
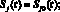
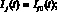
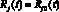
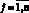 t ∈ E0. (4)
t ∈ E0. (4)
Здесь hi(t), i = 1, 2, – неотрицательная, непрерывно дифференцируемая функция. h1(t) характеризует время «инкубационного периода», в течение которого узел считается зараженным, но не распространяет вирус. h2(t) характеризует время появления нового вредоносного кода. Причем 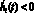 , i = 1, 2. Это значит, что функция t – hi(t) монотонно возрастает. В случае, когда hi(t) = 0, i = 1, 2, мы получаем систему обыкновенных дифференциальных уравнений без запаздывания.
, i = 1, 2. Это значит, что функция t – hi(t) монотонно возрастает. В случае, когда hi(t) = 0, i = 1, 2, мы получаем систему обыкновенных дифференциальных уравнений без запаздывания.
В построенной задаче функции Sj(t), Ij(t) и Rj(t), 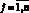 , будем считать фазовыми переменными, а управлением – скорость иммунизации
, будем считать фазовыми переменными, а управлением – скорость иммунизации 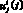 , i = 1, 2,
, i = 1, 2, 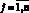 , с соответствующими ограничениями
, с соответствующими ограничениями
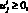 i = 1, 2,
i = 1, 2,
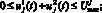
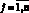 . (5)
. (5)
Здесь 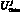 – максимальная норма управления в j-й группе, которая ограничена техническими и материальными возможностями.
– максимальная норма управления в j-й группе, которая ограничена техническими и материальными возможностями.
Данная модель (1)–(5) предполагает естественный способ расчета затрат на эпидемию. Целью управления процессом защиты от вредоносного кода является минимизация цены нанесенного ущерба и расходов на установку «иммунитета» системы.
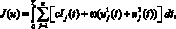 (6)
(6)
где с – относительная стоимость урона, нанесенного одной единицей инфицированного компьютера Ij(t), ω – средняя стоимость установки антивирусного программного обеспечения или межсетевых экранов.
Формализованная задача модели (1)–(6) представляет собой задачу оптимального управления системой дифференциальных уравнений с переменным запаздыванием.
Построение функции запаздывания
Рассмотрим построенную модель (1)–(6) в предположении, что антивирусное программное обеспечение обновляется через каждый промежуток времени, равный Т. Тогда получаем модель с одним временем задержки h1(t). При этом h2(t) = 0. Далее будем считать, что при t ∈ [0, Т] не осуществляется прирост новых узлов, то есть b(t) = 0 и Nj(t) = Nj = const, 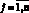 .
.
В [5] было показано, что время запаздывания является важным фактором при построении адекватной математической модели, описывающей распространение компьютерного вируса в сети.
Для построения функции запаздывания h1(t) исследуем динамику процесса. Весь период развития эпидемии можно разбить на три этапа [4, 7, 9]:
1-й этап – начало нарастания числа инфицированных компьютеров до порогового уровня.
2-й этап – эпидемия. Массовое поражение узлов и широкое распространение вируса.
3-й этап – стадия максимального подъема эпидемии, характеризуется достижением порога насыщения. В этот период зараженные узлы контактируют преимущественно друг с другом, поэтому уцелевшие узлы могут оставаться неинфицированными неопределенно продолжительное время.
Используя данную динамику эпидемии, получаем вид функции запаздывания
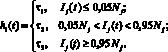 (7)
(7)
Здесь τl является величиной постоянного запаздывания, l = 1, 2, 3.
Исходя из полученной формулы (7), систему дифференциальных уравнений (1)–(3) можно представить в виде разрывной задачи в правой части с постоянным запаздыванием. Она будет иметь вид (8)
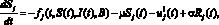
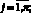
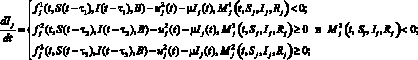
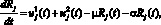
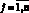 .
.
Здесь через 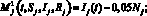
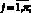
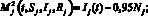
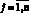 , обозначены поверхности переключения.
, обозначены поверхности переключения.
Необходимые условия оптимальности
Решение задачи оптимального управления с разрывной правой частью предусматривает рассмотрение следующих вариантов поведения траектории [1], [2]:
1) протыкание траектории поверхности переключения 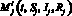 в точке
в точке 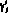 , i = 1, 2, если в любой достаточно малой окрестности точки
, i = 1, 2, если в любой достаточно малой окрестности точки 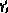 функция
функция 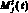 , i = 1, 2,
, i = 1, 2, 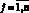 , меняет знак;
, меняет знак;
2) левостороннее или правостороннее касание траекторией поверхности переключения 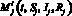 точке
точке 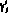 , i = 1, 2, если
, i = 1, 2, если 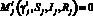 и
и 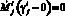 или
или 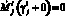 ;
;
3) скольжение траектории по поверхности переключения, если на некотором отрезке [t1, t2], 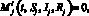 i = 1, 2,
i = 1, 2, 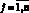 ;
;
Рассмотрим первый случай поведения траектории, а именно однократное протыкание траекторией поверхностей переключения 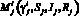 , i = 1, 2,
, i = 1, 2, 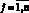 . Обозначим через
. Обозначим через 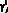 и
и  ,
, 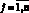 , точки переключения фазовых траекторий при пересечении поверхностей переключения
, точки переключения фазовых траекторий при пересечении поверхностей переключения 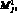
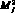 соответственно.
соответственно.
Сформулируем необходимые условия оптимальности для разрывной задачи оптимального управления с постоянным запаздыванием (рассматриваем регулярный случай) [10]. Для этого выпишем функцию Понтрягина построенной модели.
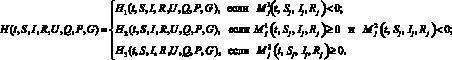
Здесь
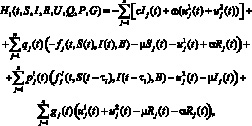
где 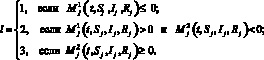
Сопряженные вектор-функции (Q(t), Pl(t), G(t)), l = 1, 2, 3, определены на промежутках 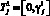 ,
, 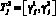 ,
, 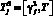 соответственно, непрерывны и почти всюду непрерывно дифференцируемы на этих отрезках.
соответственно, непрерывны и почти всюду непрерывно дифференцируемы на этих отрезках.
Теорема. Пусть 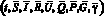 – оптимальный управляемый процесс в задаче (4) – (6), (8). Тогда оптимальное управление
– оптимальный управляемый процесс в задаче (4) – (6), (8). Тогда оптимальное управление 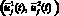 , t ∈ [0, T],
, t ∈ [0, T], 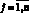 , во всех точках непрерывности доставляет максимум функции Понтрягина:
, во всех точках непрерывности доставляет максимум функции Понтрягина:
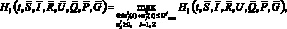 l = 1, 2, 3, где сопряженные функции являются решением системы дифференциальных уравнений
l = 1, 2, 3, где сопряженные функции являются решением системы дифференциальных уравнений
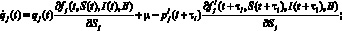
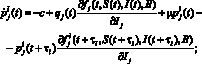 (9)
(9)
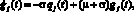
где 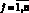 ,
, 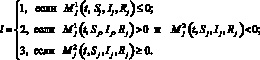
с граничными условиями на правом конце траектории
qj(T) = 0, pj(T) = 0, gj(T) = 0, 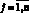 . (10)
. (10)
В точках пересечения траекторией поверхностей переключения выполняются условия скачка сопряженных функций
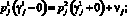
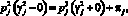
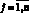

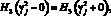
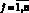 .
.
При этом величина скачка определяется по формуле
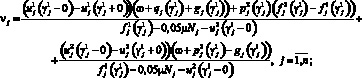
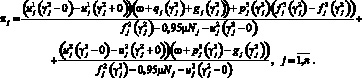
Введем функции переключения:
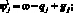
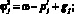
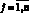 , l = 1, 2, 3.
, l = 1, 2, 3.
Из условия максимума функции Понтрягина получаем множество задач максимизации
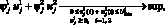
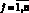 (11)
(11)
Анализ задач (11) и компактного множества ограничений для функций управления (5) позволяет найти оптимальное управление 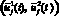 ,
, 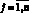 .
.
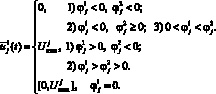
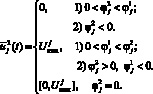 (12)
(12)
Если 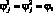
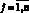 , или с учетом их определения, когда
, или с учетом их определения, когда 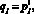
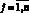 l = 1, 2, 3, то оптимальное управление будет иметь вид
l = 1, 2, 3, то оптимальное управление будет иметь вид
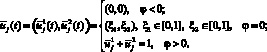
В результате получаем краевую задачу принципа максимума, состоящую из системы дифференциальных уравнений (8), (9) и краевых условий (4), (10), где оптимальное управление определяется соотношениями (12).
Выводы
В результате проведенного исследования была разработана математическая модель распространения компьютерных вирусов в локальных сетях, которая позволяет учесть «инкубационное» время заражения узла вредоносным кодом. Впервые данная модель формализована как задача оптимального управления системой дифференциальных уравнений с разрывной правой частью и с запаздывающим аргументом. Сформулированы необходимые условия оптимальности и найден вид оптимального управления, это позволит в дальнейшем объяснить и изучить различные факторы, влияющие на динамику эпидемии.
Рецензенты:
Болодурина И.П., д.т.н., профессор, заведующий кафедрой прикладной математики, Оренбургский государственный университет, г. Оренбург;
Зиятдинов Н.Н., д.т.н., профессор, заведующий кафедрой системотехники, Казанский национальный исследовательский технологический университет, г. Казань.



