В работе исследуются методы обработки и формирования сигналов в радиолокационных станциях (РЛС) с селекцией движущихся целей (СДЦ) с применением методов рандомизации грубых статистик, когда стохастичность искусственно и целенаправленно закладывается в модели сигналов и алгоритмы их обработки.
Современные исследования в области радиолокации в первую очередь идут по пути выбора вида зондирующих сигналов и совершенствования методов и средств цифровой, в общем случае пространственно-временной обработки эхо-сигналов в когерентно-импульсных радиолокационных станциях. Одно из направлений этих исследований заключается во внедрении в технику обработки и формирования радиолокационных сигналов новых цифровых технологий, поднимающих радиолокацию на новый современный уровень [1].
В работе [1] указывается, что цифровая обработка сигналов РЛС в первую очередь включает в себя дискретизацию и квантование. При этом могут использоваться различные способы этих операций:
1. Квантование во времени, обусловленное периодической структурой когерентно-импульсного сигнала и отдельных реализаций эхо-сигналов.
2. Квантование пространства по осям координат электромагнитного поля фазированными антенными решетками (ФАР) РЛС.
3. Квантование по уровню амплитуды и фазы сигналов в каналах пространственно-временной фильтрации.
4. Квантование координат и параметров движения цели, каковыми могут быть дальность, пеленг, скорость (допплеровское смещение частоты).
5. Квантование обычных и пространственных частот в апертуре ФАР РЛС, что в свою очередь связано с квантованием угловых направлений по азимуту и углу места.
6. Квантование распределений, поскольку входной пространственно-временной сигнал в процессе его наблюдения представляет собой случайный процесс, развивающийся во времени.
В данной работе, несмотря на возможность использования любого вида квантования, мы ограничились рассмотрением наиболее простого – квантования по времени. Квантование по времени превращает непрерывные функции (сигнала) y(t) в решетчатые функции y(ti).
Цифровой обработке сигналов, несмотря на известные преимущества, присущи недостатки: наличие нелинейностей амплитудных характеристик, наличие шумов квантования, округления и т.п., которые обычными способами, вытекающими из классической теории обнаружения сигналов, учесть не удается. При устранении указанных недостатков в РЛС для получения гарантированных решений необходимо учитывать не только ограничения по определению области предсказания в выборе и параметров сигналов, но и ресурсные ограничения: разрядность, частоты квантования, размеры окон пространственно-временных выборок, размеры областей предсказания и многообразие способов устранения априорной неопределенности. Одним из направлений решения данной проблемы является искусственное введение случайного процесса (рандомизации) в процедуру цифровой обработки сигналов. В настоящее время на основе такого подхода создан целый ряд устройств, реализующих различные способы обеления помех [2].
При цифровой обработке последовательность передаваемых символов является дискретным сигналом. С каждым из возможных значений символа сопоставляется некоторый набор параметров несущего колебания. Эти параметры поддерживаются постоянными в течение интервала T, то есть до прихода следующего символа. Фактически это означает преобразование последовательности чисел {nk} в ступенчатый сигнал Sn(t) с использованием кусочно-постоянной интерполяции:
Sn(t) = φ(ni);
iT ≤ t < (i + 1)T, (1)
где φ(ni) – некоторая функция преобразования набора чисел nk.
Полученный сигнал Si(t) далее используется в качестве модулирующего сигнала обычным способом. Такой способ модуляции, когда параметры несущего колебания меняются скачкообразно, называется манипуляцией. В данной работе рассматривается только пример фазовой манипуляции. При этом фазово-импульсная модуляция сигнала осуществляется в виде задержки (или упреждения) появления импульса по отношению к началу периода на время, соответствующее значению информационных символов (модулируемого сигнала). Импульсы имеют постоянную длительность. Как и в случае широтно-импульсной модуляции, частота следования импульсов сигнала является постоянной величиной. Широкое использование этого типа модуляции определяется, прежде всего тем, что отношения сигнал шум, определяемое формулой [3]
ОСШ = E0/N0, (2)
где E0 – энергия модулирующего сигнала, которая может быть рассчитана по следующему выражению:
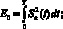(3)
N0 – двухступенчатая спектральная плотность помех рассчитывается по формуле
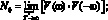(4)
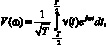(5 )
где ν(t) – сигнал помех; обеспечивают оптимальные значения характеристик ошибок.
Общий вид n-уровневой фазовой манипуляции записывается в виде
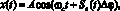(6)
где Sn(t) определяется формулой (1); Δφ – величина, на которую отличаются фазы соседних сигналов. Традиционно в радиолокации применяется «пачка модулированных сигналов», но с точки зрения статистических оценок это не имеет принципиального значения.
Цифровая обработка принятого сигнала включает в себя дискретизацию сигнала по времени и квантование по уровню. Дискретизация сигналов по времени делает систему дискретной, а квантование по уровню – нелинейной. В процессе квантования сигналов по уровню происходит процесс выделения из точно измеренного значения сигнала x(t), дискретного уровня x(iT), где T – интервал дискретизации. Этот процесс можно представить как прохождение непрерывного импульса через элемент с многоступенчатой характеристикой, т.е. через m-разрядный аналого-цифровой преобразователь (АЦП). При этом величина шага квантования h определяется соотношением
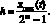(7)
В работе [2] предлагается введение искусственной стохастичности в процесс цифровой обработки сигналов, например, «рандомизации» – дискретизации сигнала по времени, которая определяется по следующей формуле:
ti = iT + ξi, (8)
где ξi – случайная величина с нулевым средним и некоторой ненулевой дисперсией σ2.
Для введения искусственной стохастичности как правило используется псевдослучайная величина, которая имеет равномерное распределение на отрезке [0, 1].
Функция плотности вероятности этой величины определяется выражением
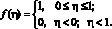(9)
Псевдослучайная величина η имеет математическое ожидание (среднее значение) M(ξ) = 0,5 и дисперсию D(ξ) = 1/12.
На рисунке представлен график функции распределения псевдослучайной величины η.
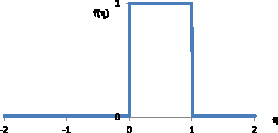
График функции распределения псевдослучайной величины η
Построение случайной величины ξi с нулевым средним и некоторой ненулевой дисперсией σ2 может быть выполнено несколькими способами. Рассмотрим некоторые из них.
Случайная величина с ξi равномерным распределением может быть построена по следующей формуле:
ξi = T(η – 0,5), (10)
где η – псевдослучайная величина, свойства которой определяются формулой (9). Псевдослучайная величина ξi, определяемая формулой (10), имеет математическое ожидание (среднее значение) M(ξ) = 0 и среднеквадратичное отклонение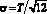 
.
Случайная величина с ξi также с равномерным распределением может быть построена по другой формуле:
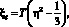(11)
где η – псевдослучайная величина, свойства которой определяются формулой (9).
Псевдослучайная величина ξi, определяемая формулой (11), имеет математическое ожидание (среднее значение) M(ξ) = 0 и среднеквадратичное отклонение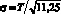 
.
Случайная величина с ξi с нормальным (Гауссовым) распределением может быть построена по следующей формуле:
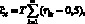(12)
где m – целое число, принимающее значение m ≥ 6; ηi – случайная величина, подчиняющаяся равномерному распределению в соответствии с формулой (9). Псевдослучайная величина ξi, определяемая формулой (12), имеет математическое ожидание (среднее значение) M(ξ) = 0 и среднеквадратичное отклонение.
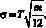(13)
Как показано в работе [2], введение искусственной стохастичности позволяет уменьшить разрядность АЦП при сохранении точности квантования. Анализ использования псевдослучайных величин, определяемых формулами (10)–(12), показал, что лучшие результаты по снижению разрядности АЦП дает распределение, определяемое формулой (12).
Основной статистической оценкой при обнаружении и различении сигналов является отношение правдоподобия, которое при использовании детерминированного сигнала на фоне белого шума выражается следующей формулой [3, 4, 5]:
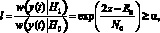(14)
где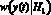 
– условная вероятность присутствия сигнала s(t) в принятом сигнале y(t) (функция правдоподобия); 
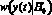– условная вероятность присутствия помех в принятом сигнале y(t); E0 – энергия сигнала s(t) и N0 – двухступенчатая спектральная плотность помех определяются формулами (3–5); z – коэффициент линейной корреляции сигнала s(t) и принятого сигнала y(t); α – некоторый уровень отношения правдоподобия.
Проведенное авторами математическое моделирование сигналов в среде Delfi7.0, параметры которых соответствуют современным РЛС, с использованием формул (3)–(14) показало, что применение искусственной стохастичности при цифровой обработке сигналов позволяет при одинаковой разрядности АЦП повысить значение критерия правдоподобия на 9–11 %.
Рассмотрим также задачу обнаружения сигналов со случайными неинформативными параметрами. При этом при разработке алгоритма обнаружения сигналов, как и в работе [1], рассмотрим наиболее простую задачу обнаружения квазидетерминированного сигнала, когда неинформативные параметры случайны, а их законы распределения вероятностей известны. В этом случае отношение правдоподобия при каждом конкретном значении параметра рассматривается как условное, а безусловное отношение правдоподобия получается путем усреднения по случайным параметрам. Пусть вектор неинформативных случайных параметров β = {β1, β2, ..., βn} имеет плотность вероятности w = w(β1, β2, ..., βn). Для получения отношения правдоподобия при наличии в сигнале неинформативных параметров необходимо в начале сформировать это отношение в предположении, что эти параметры фиксированы и известны. В результате получим отношение правдоподобия как функцию случайных параметров l = l(β1, β2, ..., βn). Далее необходимо усреднить условное отношение правдоподобия по случайным параметрам:
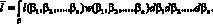(15)
Решение данной задачи также связано с реализацией возможностей использования «грубых статистик» при введении искусственной стохастичности на этапе цифровой обработки сигнала.
Отметим, что введение искусственной стохастичности существенно изменяет классический подход к задаче обнаружения сигналов, т.к. «стохастичность» в классической постановке является естественной и определяется заданными моделями отраженных сигналов, помех и собственного шума приёмника. Для сравнения в качестве базовой возьмём классическую теорию радиолокационного обнаружения сигналов, однако при этом учтём эффекты дискретизации и квантования.
Классическая задача приёма сигнала на фоне шума решается в рамках теории статистических решений. При этом сигнал подвергается ряду преобразований. В классической теории решений проектировщик системы не может управлять сигналом на входе: операция передачи задаётся внешними условиями, все сигналы определены вместе с вероятностями наступления каждого из них Введение искусственной стохастичности позволяет осуществить линеаризацию исходных нелинейных по времени данных. Предложенный метод, как и метод Монте-Карло, является инструментом, разрешающим компромисс между «дискретизацией», «грубым квантованием» и размерами окон пространственно-временных выборок.
В заключение следует отметить, что использование искусственной стохастичности при цифровой обработке радиотехнических сигналов позволяет снизить разрядность радиолокационных данных, уменьшить усреднения боковых лепестков частотных характеристик и улучшить пространственно-частотные характеристики обработки сигналов.
Рецензенты:
Бачурин В.И., д.ф.-м.н., профессор кафедры «Высшая и прикладная математика», Ярославский филиал МИИТ, г. Ярославль;
Смирнов А.Д., д.ф.-м.н., профессор, Ярославский государственный университет им. П.Г. Демидова, г. Ярославль.