Представление в аналитическом виде характеристик спектральной плотности мощности (СПМ) цифровых тестовых сигналов позволяет решать множество задач. Прежде всего это касается оценки качества передачи данных в каналах и трактах сетей связи в зависимости от выбранных способов линейного кодирования радиотехнических сигналов. В работе [4] предложена модель генератора бинарных тестовых сигналов. При этом используются тестовые сигналы с фиксированной структурой (ФС) вида R логических единиц/нулей на К битов. Структура размещения битов на цикле передачи постоянна. Например, тестовые последовательности вида «одна логическая единица на восемь битов» имеют структуру 10000000, а последовательность «две логические единицы на восемь битов» – 10001000. Стандартные полиномы, задающие структуру ПСП, описаны в рекомендациях МСЭ-Т[5]. При всех достоинствах данный подход требует обращения к специальной библиотеке, что не всегда удобно.
При дискретном характере изменения первичных (тестовых) сигналов параметры несущего колебания будут изменяться по дискретному закону (скачками). В этом случае вместо термина «модуляция» чаще используется термин «манипуляция. При этом различают три вида манипулированных сигналов: амплитудно-манипулированные (АТ – амплитудная телеграфия), частотно-манипулированные (ЧТ) и фазоманипулированные (ФТ) [2]. Все перечисленные виды сигналов находят широкое применение в радиоэлектронных системах. В данной работе будем использовать термин «несущий сигнал», если речь идет о модуляции несущей фазы последовательностью импульсов с случайным характером их следования. При разработке моделей сигналов с дискретной модуляцией будем использовать несколько видов первичных колебаний и сигналов.
Псевдослучайная структура представляет собой условно стохастическую последовательность размещения символов (для двоичной структуры битов) на цикле передачи, сформированную по заданному алгоритму[1]. В данной работе такие структуры формируются с помощью датчика случайных чисел, который автоматически встроен в программную среду Delfi. При этом псевдослучайная величина, определяемая встроенной функцией random, имеет равномерное распределение, функция плотности вероятности которого записывается в виде
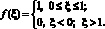(1)
Псевдослучайная величина ξ имеет математическое ожидание (среднее значение) M(ξ) = 0,5 и дисперсию D(ξ) = 1/12. Она таже имеет очень важное свойство, заключающееся в том, что вероятность попадания случайной величины в интервал (a, b) равна длине этого интервала [2]. При помощи несложных алгоритмов псевдослучайная величина, определяемая функцией random, позволяет построить случайный сигнал произвольной формы.
Рассмотрим пример формирования псевдослучайной структуры на основе двоичной системы. В этом случае система полностью задается следующими параметрами: длиной цикла передачи L (количеством бит) и временем передачи сигнала T, на основе которых определяется время дискретизации сигнала:
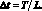(2)
Следующим шагом является построение тестового дискретного бинарного сигнала по следующему алгоритму:
1. Задается значение случайной величины ξ = random.
2. Строится тестовый сигнал по следующему правилу:
(3)
где n – порядковый номер двоичного символа в структуре (временного интервала).
Далее моделируется несущий сигнал с цифровой фазовой модуляцией по формуле
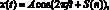(4)
где A, f – амплитуда и частота несущего сигнала.
В соответствии со свойством случайной величины ξ, определяемой функцией random, о котором шла речь ранее в этой статье, вероятность выпадения каждого значения равна 0,5. Если псевдослучайная цифровая структура имеет L символов, то вероятность образования такой структуры равна 0,5L.
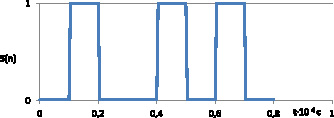
На рис. 1 представлены временные диаграммы тестового (1а) и несущего (1б) сигналов для случая бинарной псевдослучайной структуры. Несущий сигнал имеет следующие характеристики: f = 2 кГц A = 3.
Рассмотрим пример формирования псевдослучайной структуры на основе системы из трех символов. В этом случае система, так же, как и в предыдущем случае, полностью задается следующими параметрами: длиной цикла передачи L (количеством бит) и временем передачи сигнала Т.
Следующим шагом является построение тестовой дискретной структуры сигнала из трех символов по следующему алгоритму:
1. Задается значение случайной величины ξ = random
2. Строится тестовый сигнал по следующему правилу:
(5)
где n – порядковый номер двоичного символа в структуре (временного интервала).
В отличие от тестового сигнала, определяемого формулой (3), здесь используется не битовая система, а система, состоящая из трех символов.
Далее моделируется несущий сигнал с цифровой фазовой модуляцией по формуле (4).
Вероятность выпадения каждого значения равна (1/3). Если псевдослучайная цифровая структура имеет L символов, то вероятность образования такой структуры равна (1/3)L.
На рис. 2 представлены временные диаграммы тестового (2а) и несущего (2б) сигналов для случая псевдослучайной структуры из трех символов.
а
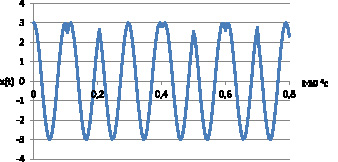
б
Рис. 1. Пример временной диаграммы тестового (а) и несущего (б) сигналов, заданных псевдослучайной бинарной последовательностью
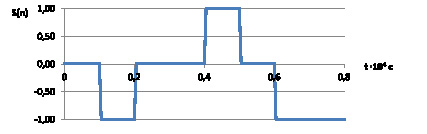
а
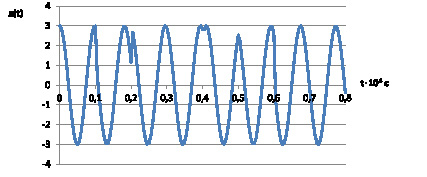
б
Рис. 2. Пример временной диаграммы тестового (а) и несущего (б) сигналов, заданных псевдослучайной последовательностью из трех символов
Рассмотрим пример формирования псевдослучайной структуры на основе системы из m символов. В этом случае система, так же, как и в предыдущем, полностью задается следующими параметрами: длиной цикла передачи L (количеством бит) и временем передачи сигнала Т.
Следующим шагом является построение тестовой дискретной структуры сигнала из m символов по следующему алгоритму:
1. Задается значение случайной величины ξ = random.
2. Строится тестовый сигнал по следующему правилу:
(6),
где n – порядковый номер символа в структуре (временного интервала).
Далее моделируется несущий сигнал с цифровой фазовой модуляцией по формуле (4).
Вероятность выпадения каждого значения равна (1/m). Если псевдослучайная цифровая структура имеет L символов, то вероятность образования такой структуры равна (1/m)L.
На рис. 3 представлены временные диаграммы тестового (3а) и несущего (3б) сигналов для случая псевдослучайной структуры из m = 5 символов.
Расчет спектральной плотности мощности (СПМ) тестового сигнала производится методом дискретного преобразования Фурье [3]:
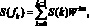(7)
где
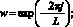(8)
S(k) – массив дискретных значений тестового сигнала, который может определяться в зависимости от условий теста по одной из формул (3), (5), (6).
Расчет СПМ выполняется в следующей последовательности:
1. Преобразование логической структуры тестовой последовательности во временную функцию с использованием программных средств Delfi.
2. Формирование массива значений модельного времени T = {T0, T1, T2, ..., TL–1} и массива значений цифрового сигнала S(k) = {S0, S1, S2, ..., SL–1}, взятых в моменты времени 0, Δt, 2 Δt, ..., (L – 1)Δt.
3. Временная дискретизация импульсов тестового сигнала и формирование массива данных (отсчетов сигнала).
4. Расчет амплитудного спектра тестового сигнала с использованием массива данных (отсчетов сигналов) и аппарата дискретного преобразования Фурье.
5. Расчет характеристик спектральной плотности мощности тестового сигнала.
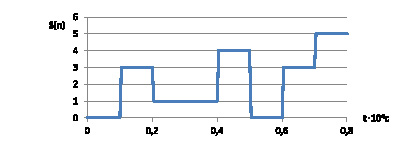
а
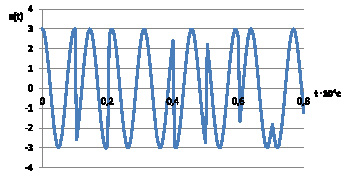
б
Рис. 3. Пример временной диаграммы тестового (а) и несущего (б) сигналов, заданных псевдослучайной последовательностью из m = 6 символов
Использование псевдослучайной величины ξ, свойства которой определяются уравнением (1), позволяет построить также абсолютно белый гауссов шум (АБГШ).
Абсолютно белый гауссов шум (АБГШ) представляет собой случайный сигнал, имеющий нормальное распределение с математическим ожиданием (средним значением) M(η) = 0 и некоторой дисперсией D(η) [2].
Согласно центральной предельной теореме, являющейся стержнем современной теории статистического моделирования [2], случайная величина η, определяемая формулой
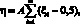(9)
где A – уровень белого шума; m – целое число, принимающее значение m ≥ 6; ξi – случайная величина, подчиняющаяся равномерному распределению в соответствии с формулой (1); имеет равномерное распределение. Причем ее математическое ожидание M(η) = 0, а дисперсия
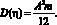(10)
Этот факт позволяет с помощью использования формулы (9) смоделировать АБГШ с заранее заданными свойствами.
Рассмотрим алгоритм построения псевдослучайного тестового сигнала, соответствующего белому АБГШ с заданными свойствами.
Исходными данными для моделирования являются A – уровень белого шума и значение дисперсии σ2.
Алгоритм выполняется в следующей последовательности:
1. В соответствии с формулой (10) определяется величина m.
2. Задается значение случайной величины ξ = random m раз.
3. Рассчитывается значение величины η по формуле (9).
4. Строится тестовый сигнал по формуле
S(n) = η. (11)
Представленный алгоритм позволяет строить математические модели АБГШ с условием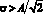 
, которое обычно выполняется для большинства встречающихся в практике радиотехнических сигналов.
Предложенная методика моделирования и расчета характеристик СПМ цифровых тестовых сигналов является аналитическим инструментом и дает возможность исследовать влияние методов линейного кодирования и форматов модуляции радиотехнических сигналов на качество их передачи.
Рецензенты:
Таршис М.Ю., д.т.н., профессор, Ярославский государственный технический университет, г. Ярославль;
Гвоздев А.А., д.ф.-м.н., профессор, Ярославский государственный университет им. П.Г. Демидова, г. Ярославль.