METHODS OF DIAGNOSING STATE OF THE OBJECT BY PUBLISHED BY ACOUSTIC NOISE

Информационные составляющие, которые содержит акустический шум объекта, является источником информации об его состоянии. Решение этой задачи может быть применено при декодировании состояний любых объектов, издающих акустический шум. На примере объектов, издающих акустический шум (пчелиных семей), рассмотрим контроль их состояний. Е.К. Еськовым [1] установлен наиболее информативный частотный диапазон от 60 до 600 Гц акустического шума пчелиной семьи.

А.Ф. Рыбочкин [2] предложил метод нахождения наиболее информативных частотных полос анализируемого частотного диапазона (60–600) Гц. Способ, основанный на использовании четырёх полосовых фильтров с шириной полосы Δf = 30 гЦ, настроенных на наиболее информативные места данного частотного диапазона, который позволяет значительно упростить программную и аппаратную реализацию диагностируемых устройств.

Рассмотрена возможность диагностирования состояний пчелиных семей путём анализа издаваемого ими акустического шума с использованием устройства, приведённого на рис. 1 [4].

Структурная схема устройства для анализа акустических шумов пчелиных семей содержит: микрофон – 1, усилитель – 2, блок узкополосных частотных фильтров – 3, блок детекторов средневыпрямленного значения – 4, микроконтроллер с аналого-цифровыми преобразователями по числу узкополосных частотных фильтров – 5, блок связи – 6, персональную электронно-вычислительную машину (ПЭВМ) – 7, блок питания – 8.

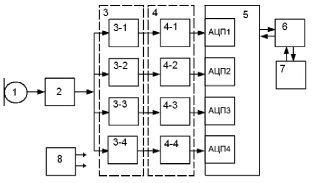
pic_47.tif

Рис. 1. Устройство для анализа акустических шумов пчелиных семей путём формирования образов спектров

Устройство для анализа акустических шумов пчелиных семей по их акустическому шуму работает следующим образом: звуковой сигнал с микрофона 1 поступает на усилитель 2. Для выделения наиболее информативных узких полос частот используется блок узкополосных частотных фильтров 3 [3–5], было применено четыре узкополосных частотных фильтра с полосами частот 205–225, 280–300, 325–345, 390–410 Гц. Выделенные сигналы с выходов узкополосных частотных фильтров 3 поступают в блок детекторов 4 средневыпрямленного значения. Детектированные значения напряжений поступают в аналого-цифровые преобразователи АЦП1, АЦП2, АЦП3 и АЦП4 микроконтроллера 5, который через блок связи 6 передает результаты аналого-цифрового преобразования на ПЭВМ 7, где происходит их кодирование и сохранение в ПЗУ. В свою очередь ПЭВМ 7 управляет работой микроконтроллера 5.

ПЭВМ 7 получает информацию в виде кодовых таблиц (табл. 1).

Дальнейшая работа с полученными данными может производиться следующими способами.

Способ № 1. Отображение состояний пчелиных семей на двумерную плоскость с соблюдением ранжированного размещения кодов.

Для создания базы данных прослушивались пчелиные семьи с различными состояниями. Далее на двумерной плоскости отображающего экрана построили координатные точки, которые характеризуют состояние пчелиной семьи.

Таблица 1

Частоты появлений кодов и их виды для установленных состояний пчелиных семей

Состояния	Реализации xi	Коды B_j и их виды, k_ji – частоты появления Bj кодов
		y_j
		B₁	B₂	B₃	…	…	B_N!–2	B_N!–1	B_N!
			…	…
А₁	1	k₁₁	k₁₂	k₁₃	…	…	K_{1 22}	K_{1 23}	k_{1 24}
А₁	n	k_n1	k_n2	k_n3	…	…	k_{n 22}	k_{n 23}	k_{n 24}
А₂	1	k₁₁	k₁₂	k₁₃	…	…	K_{1 22}	K_{1 23}	k_{1 24}
А₂	n	k_n1	k_n2	k_n3	…	…	k_{n 22}	k_{n 23}	k_{n 24}
	. .	. .	. .	…	…	…	. .	. .	. .
А_n	1	k₁₁	k₁₂	k₁₃	…	…	K_{1 22}	K_{1 23}	k_{1 24}
А_n	n	k_n1	k_n2	k_n3	…	…	k_{n 22}	k_{n 23}	k_{n 24}

В ходе анализов акустического шума пчелиных семей, а также построением точек координат схожих состояний установлено, что точки группируются на близких расстояниях, т.е. формируют класс состояния.

Способ № 2. Диагностирование состояний пчелиных семей с использованием вероятностно-статистических методов. Выявление принадлежности неизвестного состояния к известному классу состояний по минимально абсолютной разности: условных вероятностей, условных энтропий.

Первоначально необходимо накопить табл. 1 состояний А_iпчелиных семей с её диагностическими признаками с использованием устройства рис. 1.

С применением алгоритма (рис. 2) проводится вычисление координат состояний на двумерной плоскости, осуществляется построение классов состояний, также по последовательности наблюдаемых кодов строятся матрицы состояний, подсчитываются условные вероятности каждого состояния и вероятности состояний Р(А_i).

С использованием экспериментальных данных определяют апостериорные вероятности P(B_j/A_i), где событие B_j(выпадающий код) произошло при условии, что произошло событие A_iконтролируемого состояния диагностируемой пчелиной семьи. Апостериорная вероятность P(B_j/A_i) (A_i – диагностируемое i-состояние, индекс j показывает номер кода от 1 до N!) определяется согласно выражению (1) апостериорная энтропия согласно (2)

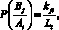mohsen17.wmf (1)

где L_i – количество кодов реализации [2].

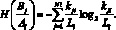mohsen07.wmf (2)

Для определения вероятности состояния Р(А_i) применим формулу

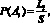mohsen18.wmf (3)

где S – суммарное количество кодов таблицы известных состояний.

Энтропия состояния определяется согласно выражению (4)

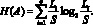mohsen08.wmf (4)

Для вычисления вероятностей появлений В_j кодов Р(В_j) применим формулу

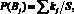mohsen19.wmf (5)

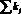где mohsen22.wmf – суммарное количество каждого В_j кода выборки всех известных состояний.

Априорная энтропия В_jкода определяется согласно выражению

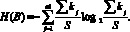mohsen09.wmf (6)

Для вычисления условных вероятностей (априорных) Р(А_i/В_j) применим формулу

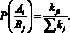mohsen20.wmf (7)

Условная энтропия определяется согласно выражению

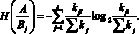mohsen10.wmf (8)

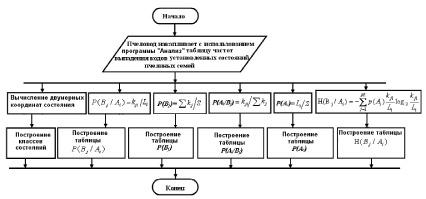
pic_48.tif

Рис. 2. Алгоритм подготовки данных для диагностирования состояний пчелиных семей

Совместная вероятность двух событий определяется по формуле

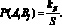mohsen11.wmf (9)

Совместная энтропия установленной выборки определяется по формуле

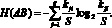mohsen12.wmf (10)

С применением формул (11, (12) проверяется сходимость табл. 5:

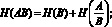mohsen13.wmf (11)

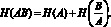mohsen14.wmf (12)

Диагностирование состояния пчелиной семьи осуществляется в течение времени от 3 до 10 минут прослушивания пчелиной семьи. Алгоритм подготовки исходных данных для диагностирования состояний пчелиных семей приведён на рис. 1. Далее установление состояния пчелиной семьи осуществляется с применением формулы

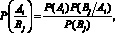mohsen21.wmf (13)

а также с применением формулы

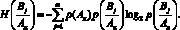mohsen15.wmf (14)

В ходе исследований для установленных состояний экспертом-пчеловодом наблюдали частоты появлений кодов, табл. 2: 1–4 пчелиные семьи в рабочем состоянии, носят мёд. 5–11 пчелиные семьи в роевом состоянии. 12–15 зимуют сильные пчелиные семьи –22 °С. 16–20 пчелиные семьи тревожит мышь. 21–24 зимуют средней силы пчелиные семьи –22 °С. 25–28 зимуют пчелиные семьи небольшой силы –22 °С. 29–30 подсадка новой матки на одной рамке, здесь же присутствует родная матка. 31–33 поведение пчёл по истечении времени – реакция пчёл на другую матку. 34–37, рамка пчёл без матки. 38–40 – реакция пчёл на новую матку, матка не принимается. 41–43 – поведение пчёл по истечении времени, матка принята.

Таблица 2

Частоты выпадения кодов установленных состояний пчелиных семей

№ п/п		04	06	07	14	46	47	54	63	67	74	76	77
1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	93	19	42	9	–	10	1	–	1	–	2	5	4
2	73	30	–	–	17	–	–	15	–	–	11	–	–
3	111	22	43	11	13	2	–	–	–	–	15	–	5
4	112	18	48	12	16	5	–	–	–	–	7	6	–
5	100	–	3	–	–	3	–	–	–	42	19	31	2
6	135	7	–	4	–	–	–	–	–	45	40	33	6
7	80	6	–	–	14	–	–	25	–	–	35	–	–
8	91	9	–	8	–	–	–	–	–	30	16	26	2
9	100	19	9	–	11	10	–	–	2	9	30	8	2
10	69	–	–	–	–	–	–	2	–	–	65	–	2
11	64	–	–	–	–	–	–	–	–	–	53	–	11
12	95	1	57	1	–	30	5	–	–	1	–	–	–
13	108	13	–	27	15	35	–	–	–	10	5	–	3
14	91	–	9	30	19	18	–	–	–	6	5	4	–
15	97	17	–	33	21	15	–	–	1	5	–	3	2
16	100	–	52	–	–	16	–	–	–	32	–	–	–
17	160	18	–	46	–	–	–	–	–	34	–	22	40
18	171	–	29	37	–	–	–	–	–	48	–	27	30
19	124	–	–	33	–	22	–	–	–	37	–	32	–
20	158	35	–	37	–	30	–	–	–	35	–	21	–
21	96	–	13	–	–	16	–	–	–	53	–	12	2
22	86	–	15	–	–	19	–	–	–	32	–	15	5
1	2	3	4	5	6	7	8	9	10	11	12	13	14
23	77	–	–	25	–	9	–	–	–	23	–	20	–
24	75	–	17	12	–	8	–	–	–	14	–	24	–
25	100	–	–	–	–	10	–	–	–	70	–	17	3
26	100	–	–	–	–	4	2	–	–	49	–	41	4
27	94	–	–	–	–	6	5	–	–	39	–	30	14
28	77	–	–	–	–	8	4	–	–	40	–	25	–
29	103	10	12	11	–	14	8	–	–	24	–	15	9
30	82	4	9	8	–	12	7	–	–	26	–	9	7
31	45	–	–	–	–	3	–	–	–	21	–	16	5
32	35	–	–	–	–	2	–	–	–	16	–	12	5
33	32	–	–	4	–	4	–	–	–	11	–	9	4
34	81	15	19	5	–	6	–	–	2	27	–	5	2
35	66	10	7	6	–	13	9	–	–	12	–	8	1
36	65	–	–	–	–	11	–	–	–	29	–	17	8
37	30	–	–	6	–	–	–	–	–	18	–	4	2
38	25	–	–	–	–	2	–	–	–	17	–	6	–
39	56	–	–	–	–	–	–	–	–	19	8	22	7
40	32	–	–	–	–	–	–	–	–	15	3	8	6
41	48	19	–	–	–	5	–	–	–	18	–	6	–
42	54	–	–	12	–	6	–	–	–	25	–	11	–
43	57	8	–	–	–	7	–	–	–	27	–	15	–
	3648	280	384	377	126	361	41	42	6	959	314	565	193

Таблица 3

Реализация кодов неизвестного состояния

L_I	04	06	07	14	46	47	54	63	67	74	76	77
82	20	35	8	1	8	–	–	1	–	3	4	2

Диагностирование неизвестного состояния пчелиной семьи (табл. 3) проведено с использованием алгоритма (рис. 3).

Определили апостериорную вероятность кодов P(B_j/A_нi) неизвестного состояния по формуле (1). Для кодов, приведённых в таблице 2, по формуле (3) вычислили априорные вероятности Р(В_j) Вычисленное значение апостериорной вероятности P(B_j/A_нi) неизвестного состояния пчелиной семьи и вычисленную априорную вероятность Р(В_j) по данным табл. 2, подставляем в формулу (5). Вероятности P(A_i) известных состояний пчелиных семей нам известны, используя данные, приведённые в табл. 2, и вычисленную апостериорную вероятность неизвестного состояния по формуле (5), осуществляем вычисление условных вероятностей состояния пчелиной семьи Р(А_i/В_j).

Используя данные известных состояний, приведённые в табл. 2, вычисляем апостериорные вероятности Р(А_i/В_j) выбранного кода по формуле (4).

Проводим вычисление разности условных вероятностей Р(А_i/В_j), вычисленных по формулам (4) и (5) Р(А_нi/В_j) – Р(А_i/В_j) = Δ_ij для каждого В_jкода состояния. Для каждого состояния вычисляется средняя разность условной вероятности состояния. Та средняя разность условных вероятностей Δ_i, которая окажется наименьшей, будет соответствовать состоянию, приведённому в табл. 2. Таким образом, мы диагностируем состояние пчелиной семьи.

Выдача диагностических сообщений выдаётся на дисплей компьютера как в виде таблиц, в виде рисунков классов состояний (рис. 4), так и в виде текста, описывающего состояние пчелиной семьи.

В ходе проведённых вычислений с использованием формул (4) и (5) анализировалась принадлежность неизвестного состояния к известному состоянию, приведённому в табл. 2.

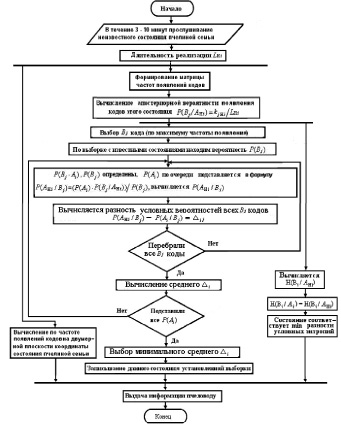
pic_49.tif

Рис. 3. Алгоритм диагностирования состояния пчелиной семьи

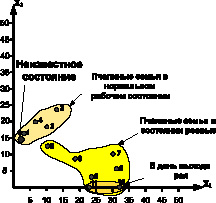
pic_50.wmf

Рис. 4. Классы состояний пчелиных семей

Абсолютная средняя погрешность в принятии решения в принадлежности к первому состоянию Δ₁ = 0,006. Тогда как при проверке принадлежности к остальным состояниям абсолютная средняя погрешность приведена в табл. 4.

С применением формулы (14) была вычислена апостериорная энтропия неизвестного состояния, которая составила H(В_j/А_нi) = 0,0585676 бит, тогда как апостериорная энтропия известного первого состояния, которая составила H(В_j/А_нi) = 0,058343 бит, т.е. минимальная разность равна 0,0002246 бит, что указывает на принадлежность неизвестного состояния к первому состоянию, приведённому в табл. 2.

Из всех приведённых средних абсолютных погрешностей условных вероятностей ΔР(В_j/А_i) самая наименьшая относится к первому состоянию.

Таблица 4

Таблица абсолютных погрешностей условных вероятностей ΔР(В_j/А_i) принятия решения в принадлежности к состоянию

Δ₁ := 0.00023	Δ₈ := 0.002:59	Δ₁₅ := 0.00197	Δ₂₂ := 0,01839	Δ₂₉ := 0.01590	Δ₃₆ := 0.00923	Δ₄₃ := 0.00878
Δ₂ := 0.00304	Δ₉ := 0,01239	Δ₁₆ := 0.02492	Δ₂₃:= 0.00916	Δ₃₀:= 0.00962	Δ₃₇ := 0.00653
Δ₃ := 0.00100	Δ₁₀ := 0.032J1	Δ₁₇ := 0.00478	Δ₂₄:= 0.00243	Δ₃₁ := 0.00855	Δ₃₈ := 0.00812
Δ₄ := 0.00068	Δ₁₁ := 0.02962	Δ₁₈ := 0.00291	Δ₂₅ := 0.02933	Δ₃₂ := 0.00639	Δ₃₉ := 0.00789
Δ₅ := 0.01173	Δ₁₂ := 0.02477	Δ₁₉ := 0.01268	Δ₂₆:= 0.02283	Δ₃₃:= 0.00159	Δ₄₀ := 0.00459
Δ₆ := 0.00849	Δ₁₃ := 0.00320	Δ₂₀ := 0.00232	Δ₂₇ := 0.01054	Δ₃₄ := 0.00351	Δ₄₁ := 0.00755
Δ₇ := 0.01232	Δ₁₄ := 0.00324	Δ₂₁ := 0.014S2	Δ₂₈ := 0.01625	Δ₃₅ := 0.00874	Δ₄₂ := 0.00789

Таблица 5

Таблица абсолютных погрешностей условных энтропий ΔР(В_j/А_i) принятия решения в принадлежности к состоянию

Δ₁ := 0.00023	Δ₈ := 0.00259	Δ₁₅ := 0.00197	Δ₂₃ := 0.00916	Δ₃₀:= 0.00962	Δ₃₇ := 0.00653	Δ₄₃ := 0.00878
Δ₂ := 0.00904	Δ₉ := 0.01239	Δ₁₆ := 0.02492	Δ₂₄ := 0.00243	Δ₃₁ := 0.00855	Δ₃₈ := 0.00812
Δ₃ := 0.00100	Δ₁₀ := 0.03251	Δ₁₇ := 0.00478	Δ₂₅ := 0.02933	Δ₃₂ := 0.00639	Δ₃₉ := 0.00789
Δ₄ := 0.00068	Δ₁₁ := 0.02962	Δ₁₈:= 0.00291	Δ₂₆ := 0.02283	Δ₃₃ := 0.00159	Δ₄₀ := 0.00459
Δ₅ := 0.01173	Δ₁₂ := 0.02477	Δ₁₉ := 0.01268	Δ₂₇ := 0.01054	Δ₃₄ := 0.00351	Δ₄₁ := 0.00755
Δ₆:= 0.00849	Δ₁₃:= 0.00320	Δ₂₀ := 0.00232	Δ₂₈ := 0.01625	Δ₃₅ := 0.00874	Δ₄₂:= 0.00789
Δ₇:= 0.01232	Δ₁₄ := 0.00324	Δ₂₁ := 0.01482	Δ₂₉ := 0.01590	Δ₃₆ := 0.00923
		Δ₂₂ := 0.01839

Из всех приведённых абсолютных погрешностей ΔР(В_j/А_i) самая наименьшая относится к первому состоянию.

На рис. 4 показано расположение неизвестного состояния, видно, что находится в непосредственной близости к первому состоянию.

Таким образом, рассмотрена возможность диагностирования состояний объекта путём анализа издаваемого им акустического шума в частотном диапазоне (60–600) Гц с использованием кодовых таблиц накапливать классы состояний. Три варианта принятия решения повышают достоверность распознавания.

Рецензенты:

Бурмака А.А., д.т.н., профессор, главный научный сотрудник НИИЦ, ФГУП «18 ЦНИИ» МО РФ, г. Курск;

Серебровский В.И., д.т.н., профессор, заведующий кафедрой электротехники и электроэнергетики, ФГБОУ ВПО «Курская государственная сельскохозяйственная академия имени профессора И.И. Иванова», г. Курск.

Scientific journal
Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

METHODS OF DIAGNOSING STATE OF THE OBJECT BY PUBLISHED BY ACOUSTIC NOISE

Fundamental research
Scientific journal | ISSN 1812-7339 | Certificate - PI №77-15598