Современные логистические складские комплексы (ЛСК) представляют собой сложно организованные хозяйственные объекты, ориентированные на управление грузопотоками большой емкости, в том числе на дистрибуцию товаров, и, вследствие этого, играют важную роль в экономической сфере деятельности. Особое внимание привлекают региональные ЛСК, так как сегодня значительное число крупных российских производственных компаний, торговых сетей и иностранных ритейлеров выбирают расширение сбыта продукции в регионах в качестве основного направления своего развития и остро нуждаются в качественных масштабных услугах складской логистики. В этой связи важнейшими задачами складского менеджмента становятся анализ и оптимизация организационно-функциональной структуры как эксплуатируемых, так и проектируемых ЛСК.
Одними из основных логистических операций складского комплекса являются погрузка и разгрузка. Оптимизация этих процессов – одна из ключевых задач системы управления ЛСК.
Для ее решения требуется определить оптимальное количество человеческих и технических ресурсов ЛСК, обеспечивающих выполнение погрузочно-разгрузочных работ (ПРР). Здесь необходимо учитывать не только потенциальные объемы работ, но и особенности загружаемой (выгружаемой) продукции, габариты транспортного средства, возможности привлечения специализированной техники и многое-многое другое. Важно сформулировать эффективное соотношение между количеством требуемых постов, объемом поставок, числом обслуживающего персонала и расходами на строительство каждого отдельного поста.
Верное решение по количеству технических и трудовых ресурсов ЛСК, направляемых на выполнение работ по разгрузке товаров, позволит, с одной стороны, снять проблему очередей транспортных средств, с другой – сократить простой персонала ЛСК, то есть позволит повысить надежность и экономичность работы ЛСК.
Целью исследований, представленных в данной статье, является разработка имитационной модели, обеспечивающей определение предпочтительных уровней обслуживания клиентов ЛСК при выполнении ПРР.
Модель предпочтительного уровня обслуживания
В современных условиях для повышения эффективности функционирования сложных систем главной задачей зачастую становится максимизация уровня качества логистических услуг при одновременном снижении затрат на его обеспечение. Многообразие параметров качества, их противоречивость, сложность формализации усложняют процесс его оценки. Для адекватного отображения качественных характеристик в математической модели функционирования сложной системы необходимо определить метод их перевода в количественные параметры.
Анализ и оценку эффективности проведения ПРР можно провести, используя модель предпочтительного уровня обслуживания [6]. Идея состоит в определении приемлемого интервала изменения уровня обслуживания путем поиска разумных пределов для конкурирующих экономических показателей, которые характеризуют процесс обслуживания. Эти пределы представляют собой уровни предпочтительного обслуживания, которых стремится достичь лицо, принимающее управленческое решение.
При определении уровня предпочтительного обслуживания ПРР в ЛСК с несколькими сервисами можно рассмотреть два конкурирующих экономических показателя процесса обслуживания: среднее время W ожидания в системе и процент X простоя сервисов. Задача сводится к определению числа сервисов с, для которого выполняется условие W ≤ α и X ≤ β, где α и β – уровни предпочтительного обслуживания, определенные лицом, принимающим управленческое решение.
Графически решение задачи можно найти, построив зависимости среднего времени ожидания и процента простоя сервисов от количества сервисов (рис. 1). Отмечая на графике значения α и β, можно определить приемлемый интервал изменения значений для уровня обслуживания с.
Если оба упомянутых выше условия нельзя удовлетворить одновременно, необходимо ослабить один или оба уровня предпочтительности, пока не будет получен приемлемый интервал изменения количества сервисов. Рассмотренные показатели являются измерителями качества обслуживания потребителей. Их определение, контроль и оценка позволяют также оценить эффективность системы обслуживания ЛСК.
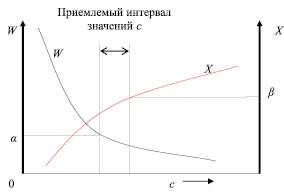
Рис. 1. Приемлемый интервал изменения значений для уровня обслуживания
Неформальная постановка задачи
ЛСК предоставляет услуги по проведению ПРР при использовании авто- и железнодорожного транспорта различной грузоподъемности. Существуют нормативы проведения ПРР с учетом вида грузового транспорта, вида и категории груза. Невыполнение данных нормативов влечет за собой штрафные санкции. Необходимо определить такое количество ресурсов ЛСК (человеческих и технических), чтобы среднее время ожидания транспортом ПРР было меньше α, процент времени простоя персонала ЛСК не превышал β, экономические показатели оставались в допустимых пределах.
Характеристики имитационной модели
Для решения поставленной задачи была разработана имитационная модель процесса проведения ПРР ЛСК. Модель реализована на языке General Purpose Simulation System (GPSS) [5]. Для выполнения модели использована система GPSSS World [3]. Характеристики модели представлены в табл. 1.
На рис. 2 представлена блок-схема фрагмента имитационной модели – сегмента, моделирующего поступление и обслуживание транспортного средства i-го вида по случайным заявкам. Транспортное средство поступает в систему в соответствии с равномерным законом распределения. Время поступления анализируется. Если система доступна, определяются коэффициент К1 загруженности ТС, вид работ (погрузка или разгрузка) и ТС становится в очередь. Моделируется занятость и освобождение многоканального устройства BR, вычисляются и суммируются с предыдущими значения наблюдаемых переменных: время T-prr погрузки/разгрузки, доход Dohod от выполнения ПРР, штраф Shtraf за несоблюдение временных норм проведения работ, грузооборот склада Gruz. Разработка и применение имитационной модели осуществлялись в соответствии с методикой, предложенной в [1].
Вычислительный эксперимент
Диапазоны и шаг изменения входных переменных были определены заказчиком. Тем самым было обусловлено большое количество наблюдений. Поэтому был проведен частичный факторный эксперимент. Многовариантные расчеты проводились в распределенной вычислительной среде, которая включала кластеры, организованные на базе персональных компьютеров и функционирующие под управлением операционной системы Windows и системы управления прохождением заданий Condor [4]. Выборочные результаты моделирования приведены в табл. 2.
На основе вышеприведенных результатов можно сделать вывод, что при проведении ПРР целесообразно использовать 3 бригады. Это значительно сокращает среднее время нахождения транспортного средства в очереди. В этом случае коэффициент простоя и требуемые экономические показатели остаются в допустимых пределах.
Результаты моделирования, полученные в рамках вычислительного эксперимента, были использованы в управленческих службах ООО «Иркутский хладокомбинат» при разработке нормативов ПРР и определении категорий «лояльных» клиентов.
Таблица 1
Характеристики модели
|
Характеристика |
Описание характеристики |
|
Транзакты |
Транспортные средства (ТС) различной грузоподъемности (5 видов) |
|
Приборы |
Бригады, участвующие в ПРР (каждая бригада включает: 2 грузчика, 2 водителя электропогрузчиков) |
|
Модельное время |
43 200 минут (1 месяц) |
|
Входные переменные |
Накладные расходы по проведению ПРР для каждого типа ТС; цена ПРР на 1 кг груза (зависит от вида груза); зарплата бригады; нормы времени ПРР на каждый тип ТС с учетом вида груза; величина штрафа за простой ТС |
|
Наблюдаемые величины |
Доход от ПРР; себестоимость ПРР; штраф за простои ТС; прибыль от ПРР; рентабельность ПРР; грузооборот ЛСК; процент времени простоя бригад; среднее время ожидания ТС обслуживания. |
|
Особенности модели |
Разнородные ТС, включая железнодорожный транспорт; различная рентабельность; различные нормы времени проведения ПРР; различные виды груза; наличие недоступности сервисов, обусловленных человеческими факторами, техническими неисправностями. |
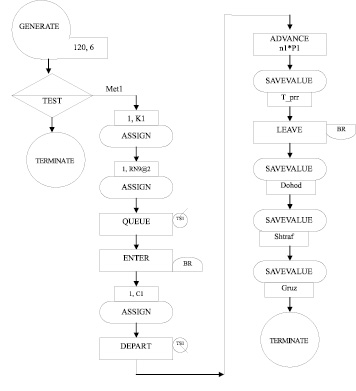
Рис. 2. Блок-схема фрагмента имитационной модели
Таблица 2
Результаты моделирования
|
Показатель |
Количество бригад |
|||
|
2 |
3 |
4 |
5 |
|
|
Коэффициент изменения дохода |
1,04 |
1,06 |
1,08 |
1,11 |
|
Коэффициент изменения себестоимости |
0,78 |
0,88 |
0,98 |
1,18 |
|
Коэффициент изменения прибыли |
0,26 |
0,19 |
0,11 |
– 0,07 |
|
Рентабельность, % |
33,55 |
21,19 |
10,75 |
– 5,61 |
|
Коэффициент простоя |
0,28 |
0,30 |
0,31 |
0,32 |
|
Среднее время в очереди, мин |
4,86 |
2,04 |
2,02 |
1,95 |
Модифицированная версия рассмотренной имитационной модели использована для классификации потоков вычислительных заданий и ресурсов экспериментальной кластерной Grid ИДСТУ СО РАН. Для каждого класса заданий был определен уровень обслуживания, а также допустимые интервалы изменения значений показателей эффективности функционирования Grid. Полученные результаты [2] показали, что дополнительное применение классификации заданий в процессе распределения заданий совместно с традиционными метапланировщиками заданий Grid дает возможность повысить коэффициент полезного использования вычислительных ресурсов системы на 15–18 %.
Заключение
Результаты исследования обеспечивают дополнительные функциональные возможности для систем управления ЛСК и ориентированы на подготовку и проведение экспериментов с помощью высокопроизводительных вычислений с целью ускорения получения результатов для принятия эффективных логистических решений. В плане развития модели предполагается введение в нее новых сегментов, входных переменных и наблюдаемых величин. Модифицированные версии модели могут быть успешно использованы для исследования широкого спектра сложных систем с целью определения предпочтительных уровней обслуживания требований.
Исследование выполнено при частичной финансовой поддержке РФФИ, проект № 15-29-07955-офи_м.
Рецензенты:
Данеев А.В., д.т.н., профессор кафедры «Информационные системы и защита информации» Иркутского государственного университета путей сообщения, г. Иркутск;
Опарин Г.А., д.т.н., профессор, зам. директора по научной работе ФБГУН «Институт динамики систем и теории управления им. В.М. Матросова» СО РАН, г. Иркутск.



