Расчет показателей надежности лесовозных автопоездов производится на основании анализа отказов, зафиксированных у подконтрольных автомобилей, с помощью известных методов теории вероятностей и математической статистики.
Для построения целевой функции (1) необходима статистическая информация 3 видов:
– информация, позволяющая выявить операции, для которых целесообразно корректирование периодичности;
– информация, с помощью которой можно построить математическую модель зависимости величины суммарных удельных приведенных затрат на техническое обслуживание и ремонт автомобилей (агрегатов) от периодичности выполнения выявленных операций;
– информация, позволяющая построить математические модели, описывающие связь показателей надёжности и функциональных показателей с периодичностью выполнения операций технического обслуживания.
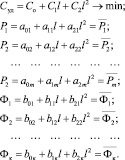 (1)
(1)
Для получения информации первого вида целесообразно использовать результаты наблюдений за группой автомобилей, эксплуатирующихся в исследуемом хозяйстве. Целью этих наблюдений является выявление таких операций технического обслуживания, периодичность выполнения которых в наибольшей степени оказывается на удельные затраты, показатели надежности и показатели функциональных свойств. Этой цели соответствует план NRT [11]. Для получения достаточно объективных данных при корректировании режимов ТО количество подконтрольных автомобилей должно быть не менее 10–15 м и может быть не более 20–25, а продолжительность наблюдения не менее 3–6 месяцев [2]. При анализе влияния периодичности выполнения операций ТО на перечисленные показатели можно также использовать парный корреляционный анализ.
В качестве показателя тесноты связи используется корреляционное отношение, определяемое по формуле
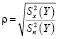 , (2)
, (2)
где
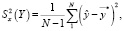 (3)
(3)
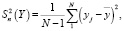 (4)
(4)
где 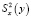 – дисперсия отклонения линии регрессии от общей средней;
– дисперсия отклонения линии регрессии от общей средней;
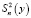 – полная дисперсия зависимой переменной (удельных затрат, показателя надежности, функционального показателя); N – объем наблюдений.
– полная дисперсия зависимой переменной (удельных затрат, показателя надежности, функционального показателя); N – объем наблюдений.
Для оценки значимости корреляционного отношения используется критерий Стьюдента, вычисление которого производится по формуле
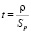 , (5)
, (5)
где 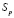 – среднеквадратичное отклонение корреляционного отношения.
– среднеквадратичное отклонение корреляционного отношения.
Связь между рассматриваемыми величинами является существенной в том случае, если расчетное значение t больше табличного при уровне значимости α = 0,05.
В результате проведенного анализа из перечня операций по обслуживанию узлов, агрегатов и систем, лимитирующих надежность автомобиля, выделяются операции оказывающие существенное влияние на критерий оптимизации и рассматриваемые показатели. Эти операции группируются по видам и условиям выполнения с учетом возможности установления для каждой группы единой периодичности.
Далее для каждой группы операций определяется состав ограничений, накладываемых на целевую функцию (1). Для этого определяются показатели надежности и функциональные показатели, которые зависят от периодичности выполнения рассматриваемых операций, и обосновываются нормативные значения этих показателей. Информация, необходимая для оценки коэффициентов регрессии уравнений, входящих в построенную целевую функцию, собирается по результатам эксплуатации группы подконтрольных автомобилей, имеющих различную периодичность выполнения рассматриваемых групп операций. В качестве середины интервала можно взять периодичность, рекомендуемую положением. Нижние и верхние границы устанавливаются для каждого конкретного случая с таким расчётом, чтобы оптимальная периодичность лежала в пределах рассматриваемого интервала.
Количество подконтрольных автомобилей принимается с таким расчётом, чтобы получаемая информация обеспечивала эффективность применения методов корреляционного анализа. В рассматриваемом случае число коэффициентов регрессии равно трем. Поэтому объем выборки должен быть не менее 15–21 шт. В связи с тем, что при эксплуатации возможна потеря информации по различным причинам, количество подконтрольных автомобилей должно быть не менее 25 шт.
Периодичность выполнения рассматриваемых операций ТО для подконтрольных автомобилей устанавливается таким образом, чтобы ее значения варьировались в пределах принятого интервала.
При выборе подконтрольных автомобилей необходимо, чтобы условия их работы были типичными для данной модели. Несмещенность оценок параметров целевой функции обеспечивается за счет получения при испытаниях подконтрольных автомобилей вероятностного аналога моделируемой зависимости.
В процессе наблюдений для каждого подконтрольного автомобиля определяются удельные затраты на техническое обслуживание и ремонт, значения показателей надежности и функциональных показателей, включенных в целевую функцию.
Определение функциональных показателей производится путем непосредственного их измерения или с помощью существующих способов диагностики.
При определении удельных затрат на ТО и ремонт значения показателей надежности и функциональных показателей включены в целевую функцию.
Определение функциональных показателей производится путем непосредственного их измерения или с помощью существующих способов диагностики.
Переменными затратами являются затраты на оплату труда ремонтного персонала Cтр, на запасные части и материалы Cзч. Кроме того при изменении объема ТО и ТР будет меняться объем капитальных вложений. Поэтому переменные затраты будут равны
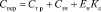 . (6)
. (6)
Определение расходов на запасные части и материалы, используемые при ТО и ТР, производятся по формуле
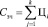 , (7)
, (7)
где Цi – стоимость j детали или материала по прейскуранту; j – количество материалов и деталей, заменяемых на рассматриваемом интервале пробега.
Затраты на оплату труда ремонтного персонала определяются
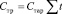 , (8)
, (8)
где Cтар – средняя тарифная ставка ремонтных рабочих; 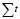 – суммарная трудоемкость технического обслуживания и ремонта на интервале пробега.
– суммарная трудоемкость технического обслуживания и ремонта на интервале пробега.
Определение капитальных вложений на техническое обслуживание и текущий ремонт производится по формуле
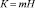 , (9)
, (9)
где H – норма капитальных вложений на одного производственного рабочего; m – количество рабочих, необходимых для обслуживания и ремонта подконтрольного автомобиля на интервале пробега.
Величина m рассчитывается по формуле
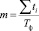 , (10)
, (10)
где 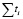 – суммарная трудоемкость ТО и ремонта в рассматриваемом интервале пробега; Тф – фонд времени ремонтных рабочих за этот период. Для получения удельных затрат, полученное значение Cпер делится на интервал пробега.
– суммарная трудоемкость ТО и ремонта в рассматриваемом интервале пробега; Тф – фонд времени ремонтных рабочих за этот период. Для получения удельных затрат, полученное значение Cпер делится на интервал пробега.
После определения для каждого подконтрольного автомобиля значений функциональных показателей, показателей надежности и удельных затрат полученная информация представляется в виде матрицы:
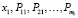 ,
, 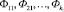
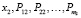 ,
, 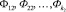 (11)
(11)
… … … …
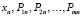 ,
, 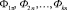 ,
,
где 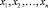 – значения периодичностей у подконтрольных автомобилей;
– значения периодичностей у подконтрольных автомобилей; 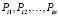 – значения показателей надежности подконтрольных автомобилей;
– значения показателей надежности подконтрольных автомобилей;
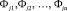 – значения функциональных показателей подконтрольных автомобилей.
– значения функциональных показателей подконтрольных автомобилей.
Матрица исходных данных (11) используется для нахождения коэффициентов регрессии моделей, входящих в целевую функцию (1).
Основная задача состоит в определении коэффициентов регрессии уравнения
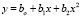 . (12)
. (12)
В данном случае задача оценивания bi представляет собой нахождение криволинейной регрессии по методу наименьших квадратов.
С помощью системы ортогональных полиномов Чебышева уравнение (12) можно представлять в следующем виде:
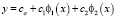 . (13)
. (13)
Для этого уравнения формулы для вычисления полиномов Чебышева будут иметь вид
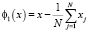 , (14)
, (14)
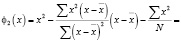
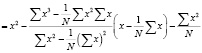 .
.
Значения коэффициентов, входящих в уравнение (14), определяются по формулам
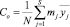 , (15)
, (15)
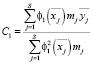 , (16)
, (16)
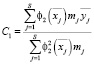 , (17)
, (17)
где S – число интервалов изменения периодичностей выполнения операций ТО; 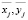 – среднее значение величин x и y в j интервале; mj – количество автомобилей, у которых периодичность находится в j интервале.
– среднее значение величин x и y в j интервале; mj – количество автомобилей, у которых периодичность находится в j интервале.
Проверка адекватности построенного уравнения производится с помощью F-критерия. При соблюдении условия (17) гипотеза об адекватности принимается
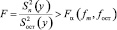 , (18)
, (18)
где 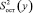 – остаточная дисперсия, характеризующая рассеивание экспериментальных точек относительно линии регрессии;
– остаточная дисперсия, характеризующая рассеивание экспериментальных точек относительно линии регрессии;
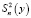 – полная дисперсия, характеризующая рассеивание точек около общей средней.
– полная дисперсия, характеризующая рассеивание точек около общей средней.
Значения 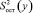 и
и 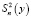 определяем по формулам
определяем по формулам
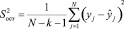 , (19)
, (19)
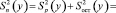
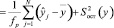 , (20)
, (20)
где k – порядок параболы (в рассматриваемом случае = 2); fp – число степеней свободы, соответствующее дисперсии регрессии.
Значения fn и fост вычисляются по формуле fn = N – 1, fост = m – 1. В случае адекватности уравнений построенная целевая функция используется для расчёта оптимальной периодичности. Если условие адекватности не соблюдается, то в многочлены вводятся добавочные члены, после чего вновь рассчитываются коэффициенты регрессии и определяется адекватность уточненной модели. Этот процесс последовательно повторяется до тех пор, пока не будут получены модели, удовлетворяющие условию адекватности.
Для отыскания минимума построенной целевой функции могут быть использованы различные методы. Выбор того или иного из них определяется видом функции и ее ограничениями.
В данном случае целевая функция нелинейна, непрерывна и имеет ограничения в виде неравенств. Характерной ее чертой является непрерывная дифференцируемость. Для оптимизации подобных функций целесообразно использовать методы дифференциального исчисления. Целевая функция (1) является строго выпуклой. Ее минимум достигается в точке А, где частная производная равна нулю. В общем случае минимум может лежать как внутри, так и за пределами допустимой области, определяемой характером накладываемых на целевую функцию ограничений.
В том случае, если минимум находится в допустимой области, точка А определяет оптимальную периодичность выполнения операций ТО. Если же минимум целевой функции находится вне допустимой области, то минимум целевой функции лежит на ее границе. Для решения задачи в этом случае необходимо определить значения целевой функции на границах допустимой области, выбрать из них минимальные и определить соответствующую этому значению функции периодичность выполнения операций ТО.
Рецензенты:
Павлов А.И., д.т.н., профессор, профессор кафедры лесных, деревообрабатывающих машин и материаловедения, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта.
Сушков С.И., д.т.н., профессор кафедры технологии машин и лесозаготовок, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта.



