Структура рыночной экономики предполагает развитую систему взаимосвязанных рынков, охватывающих обеспечение производства товаров и услуг, элементы материального и денежного обращения, потребительского рынка, рынков технологий и духовных благ. В классической модели рыночная экономика представляется как система нескольких взаимодействующих рынков: рынка производства товаров, рынка трудовых ресурсов, финансового рынка и других. В равновесии каждый из рынков описывается кривыми спроса и предложения соответствующих продуктов, пересечения которых определяют точки динамического равновесия. Отклонения от равновесия любого из рынков считаются малыми и в моделях установления нового равновесия обсуждаются лишь качественно [1, 2].
Важнейшей сферой макроэкономики является производство, наполняющее рынки товарной массой и определяющее формирование рыночных отношений. Между производством и потреблением товаров и услуг функционирует система распределения, определяемая сложившимися социальными отношениями в обществе. Детализация объектов рынков и связей делает возможным построение моделей социально-экономических процессов, что предоставляет исследователю возможность формализации теории процессов. Классическая модель рыночной экономики представляет макроэкономическую систему как взаимодействие трёх рынков: производства товаров, рынка трудовых ресурсов и финансового рынка [1, 2].
Моделирование социально-экономических процессов и объектов часто связывают с получением численных результатов, например в теории исследования операций, теории игр, в которых вводится целевая функция. Современный социально-экономический анализ не приводит к адекватному описанию сложных многопараметрических макроэкономических систем. Принцип оптимальности, широко используемый в большинстве математических работ по моделированию, эффективен не всегда, в силу отсутствия или сложности динамических экономических моделей неравновесных, открытых, самоорганизующихся систем. Такие проблемы, как автоколебания параметров, наличие у них быстрых изменений и скачков (катастроф), не описываются в моделях с использованием принципов оптимальности [2, 3].
Качественная феноменологическая теория социально-экономических процессов ставит своими целями нахождение простейших моделей, описывающих данные системы и процессы в них. Эти модели могут восстанавливаться по динамическим рядам параметров исследуемых систем в виде регрессионных моделей. В динамических моделях проводится математический анализ возможных сценариев их поведения с помощью существующих методов (бифуркационный анализ, теория катастроф) и выдача рекомендаций для оптимизации процессов. Задачи качественного анализа делают акцент на получении качественного результата, на исследовании характерных черт всего явления, на прогнозировании явления [2–6].
Синергетические модели экономических процессов
В синергетических моделях рыночной экономики полагается, что субъекты являются открытыми и неравновесными и обмениваются информацией. Обмен информацией и взаимодействие с окружением может приводить к понижению энтропии в системе, что ведёт к появлению новых равновесных состояний и структур, изменениям с образованием новых форм в организации системы. Наряду с эволюционным, медленным изменением иногда в системе возникает динамический хаос с последующей самоорганизацией новых оптимальных структур. Хаотическое поведение экономических параметров рынков вблизи точек экономических катастроф описывают в нелинейной динамике сложных систем странными аттракторами [2]. Аттракторы в дальнейшем развитии превращаются в другие формы самоорганизации: в циклические колебания экономических параметров, стремление фазовых траекторий систем в устойчивые или неустойчивые состояния типа узлов и фокусов. Математический анализ нелинейных моделей проводится с помощью существующих методов бифуркационного анализа и теории катастроф [2, 3].
Качественное исследование моделей состоит в изучении топологических структур, на которые разбивается фазовый портрет системы. Сущностный анализ состоит в сопоставлении неприводимых структур фазового портрета конкретным объектам и процессам, происходящим с ними, совместно с бифуркационным анализом стационарных точек [2]. При макроэкономическом анализе динамических процессов используют ряд связанных, нелинейных дифференциальных уравнений для экономических параметров. Отбор нелинейной математической модели функционирования предприятий может быть решён лишь с помощью анализа наилучшего совпадения прогнозов, даваемых моделями с наблюдаемыми динамическими рядами. Динамические ряды данных предприятий анализируются на стационарность и при наличии значительных девиаций дисперсии, поведение динамической системы должно описываться дифференциальными уравнениями. Необходимо проводить обработку рядов для нахождения коэффициентов дифференциальных уравнений, выбираемых как пробные математические модели системы [2].
Пусть рассматривается экономическая система, поведение которой описывается системой дифференциальных уравнений первого порядка
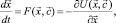(1)
где вектор 
задает состояние динамической системы набором существенных переменных – «параметров порядка»; 
– вектор управляющих параметров; U – потенциал Тома [2], моделирующий характер поведения системы вблизи экономической катастрофы. Фазовая траектория такой системы стремится к единственному предельному состоянию, которым может быть замкнутая траектория, некоторая точка или многообразие – аттракторы. В процессе изменения потенциала U изменится как сама система, так и ее интегральные кривые в фазовом пространстве. Важно проследить за характером изменения стационарных особых точек потенциала U, которые называются множеством катастроф, в которых происходит существенное изменение поведения системы.
Если выделить существенные, медленно меняющиеся параметры модели, её параметра порядка (ПП) η, можно найти из (1) динамические уравнения, в которые войдут соответствующее ПП сопряжённые им поля h, а в уравнения для h войдут параметры внешних воздействий или управляющие параметры S, для которого можно получить соответствующие уравнения [4]. Таким образом, простая математическая модель представляет собой дифференциальные уравнения для параметров порядка (ПП) η, сопряжённых им полей h и параметров внешних воздействий или управляющих параметров S:
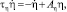
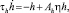(2)
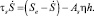
Здесь Aη, Ah, As – константы связи; Se – стационарный управляющий параметр; τη, τh, τs – времена релаксации параметров порядка, сопряжённых полей и управляющих параметров соответственно. В синергетике модель (2) называется моделью Лоренца, которая в наиболее простой и изученной форме описывает динамическое состояние хаоса. Этот аттрактор получил название аттрактор Лоренца и является наиболее изученной и популярной математической моделью, демонстрирующей поведение типа динамический хаос. Она же описывает и процесс самоорганизации систем из динамического хаоса при переходе в режим регулярного эволюционного поведения [2, 3].
Рассмотрим динамику систем в области катастроф в приближении стандартного синергетического подхода, учитывающего принцип соподчинения степеней свободы выделенным – ПП. В этом режиме выполняются следующие неравенства в иерархии времён релаксации: τη >> τh, τs, а временная зависимость сопряжённого поля и внешних параметров определяется изменением ПП: h(t) = h(η(t)) и S(t) = S(η(t)). При выполнении принципа подчинения поведение системы описывается уравнениями (2), в которых внешнее поле и управляющий параметр выражены через ПП. Когда параметр внешнего воздействия Se меньше критического значения Sc = (AηAh)–1, потенциал U(η) имеет минимум в точке η0 = 0 и упорядочения в системе не происходит. В закритической области при Se > Sc в минимуме потенциала катастроф система имеет ненулевой ПП [2]
η0 = ηm(Se/Sc – 1)1/2, (3)
где ηm–2 = AsAh и стационарное значение ПП возрастает с критическим показателем ½ при закритическом значении безразмерного параметра внешнего воздействия до s = Se/S > 1. В закритическом режиме образуется область точек, притягивающая фазовые траектории, к которой система движется быстро, но при попадании в неё движение замедляется. Указанное множество, называемое «руслом», и соответствует эволюционному поведению системы [3].
Модели экономических предприятий с инновационной деятельностью
Исследуем влияние инновационной деятельности на динамику систем в области катастроф. Рассмотрим известную систему открытой трёхсекторной модели функционирования экономической системы, в которой учтём инновационную деятельность активной части работников и менеджеров предприятий в трёх секторах: производственном, характеризуемом выпуском продукции – x(t), имеющим трудовые ресурсы – y(t), располагающим финансовыми ресурсами – z(t) [4, 5]. Творческую активность по созданию новых инновационных технологий будем учитывать функцией m(t), которая даёт удельную характеристику эффективного изменения способов производства. Такой вариант открытой трёхсекторной модели функционирования экономической системы описывается системой уравнений для основных параметров секторов:
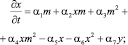
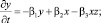(4)
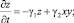
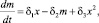
здесь α5x и α6x – непроизводственные расходы системы; α7y – прирост валового продукта, связанный с производительностью труда; β1y – выбывание трудовых ресурсов в процессе производства; β2y – изменение трудовых ресурсов, связанное с ростом валового продукта; β3xz – вовлечение трудовых ресурсов в связи с инвестициями и дополнительным производством товаров; γ1z – доходы; γ2xy – доход системы, связанный с ростом производства и ресурсов. Параметр m(t), характеризующий эффективность управления предприятием, связанную с внедрением инновационных способов производства, меняющийся в интервале 0 < m < 1 и определяемый относительным количеством принятых на предприятии инноваций, увеличивающими прибыль, описывается последним уравнением в системе (4). Члены системы: α4xm2 – планирование затрат капитала на проведение научных и инженерных инноваций; коэффициент α2 – эффективность инновационной деятельности; α2xm – инновационные капитальные вложения в основные фонды. В последнем уравнении системы (4) член δ1x – отражает увеличение вариантов инновационных производств; δ2m – уменьшение числа способов производства, оказавшихся неэффективными; δ3x2 – влияние вложений капитала в инвестиции, приносящие прибыль. Коэффициенты α1, β1, γ1, δ1 системы уравнений (4) определяют времена релаксации параметров x, y, z, m в режиме гладкой эволюции к квазиравновесным значениям для производственного, трудового и финансового рынков. Переход к обезразмеренным параметрам в системе уравнений (4) при определённых значениях коэффициентов системы уравнений приводит к модели Лоренца и решениям типа динамического хаотического поведения.
Рассмотрим механизмы, стабилизирующие хаотическое или неустойчивое поведение экономических систем. Рассмотрим случай, когда происходит быстрая релаксация степеней свободы параметров y и z, так что они входят в первое и последнее уравнения системы (4) своими квазиравновесными значениями. В этом случае имеем из (4)
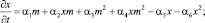
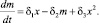(5)
Имеются два стационарных ненулевых решения x1,2 системы уравнений (5). Исследуем фазовой диаграммы возможных структур коллективизированного поведения экономических систем. Бифуркационный анализ корней характеристического уравнения (5) показывает, что при
α5δ2 > α1δ1 (6)
в укороченной модели (5) существует единственное положительное стационарное состояние равновесия x1, m1. При выполнении условий для коэффициентов системы (5)
α5δ2 < α1δ1,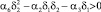 
(7)
в модели таких положений два. Коэффициенты характеристического уравнения σ, μ для исследования корней системы (5), определяющих границы раздела на фазовой диаграмме неустойчивых решений типа седло, устойчивых и неустойчивых решений типа узел, седло и предельных циклов имеют вид
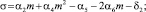(8)
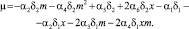(9)
Исследование соотношения (8), (9) показывает, что первое положительное стационарное состояние может быть устойчивым фокусом; устойчивым фокусом, который окружает неустойчивый предельный цикл; неустойчивым фокусом, вокруг которого есть единственный предельный цикл; неустойчивым фокусом без цикла. При μ < 0 все решения системы (5) – неустойчивые решения типа седло. Второе положительное состояние равновесия при выполнении условия (7) для μ > 0 всегда устойчиво и предельных циклов не имеет. Следовательно, параметры инновационной модели (5) дают возможность появления устойчивого эволюционного развития.
Модели конкурентного рынка
Технический прогресс общества обеспечивается конкурентной борьбой предприятий с инновационной технологией, повышающей качество и производительность труда, с предприятиями, выпускающими продукцию с устаревшей технологией. На модели конкурентной борьбы возможно проследить этапы конкуренции и понять варианты возможных её исходов. Пусть x(t) – концентрация предприятий в момент времени t, выпускающих продукцию по устаревшей, но общепринятой технологии, а n(t) – концентрация предприятий, внедривших инновационные технологии. Система дифференциальных уравнений для скорости изменения числа этих предприятий при конкурентной борьбе имеет вид
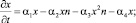(10)
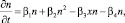(11)
здесь α1x и β1n – естественный прирост числа фирм обоих типов со скоростями α1 и β1; члены α4x и β4n – естественное уменьшение количества предприятий; члены –α2xn и –β3xn характеризуют уменьшение количества предприятий в результате их конкурентной борьбы; член –α3x2n характеризует убыль фирм со старой технологией в результате их большой плотности при ограниченном спросе и в результате конкуренции между собой и с предприятиями, обновившими свои технологии; член β2n2 – нелинейный рост числа фирм, обеспеченный инновационными технологиями.
Рассмотрим начальный этап зарождения предприятий с новой технологией, когда они ввиду малочисленности не представляют серьёзную конкуренцию n << x и положим α2 в правой части уравнения (10) равным нулю. Проведём анализ возможных решений системы уравнений (10), (11) с помощью характеристического уравнения. В нашем приближении можно получить для коэффициентов квадратичного характеристического уравнения выражения
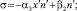(12)
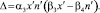(13)
Здесь x′ и n′ – положения равновесия модели. При условии (β3x′ – β4n′) > 0 реализуется фазовая траектория типа седло. Таким образом, наша модель стала неустойчивой, как только появилась хоть одна фирма, использующая инновационную технологию выпуска продукта. В модели есть бифуркация, связанная с членом β2n2, которая приводит к исчезновению предприятий, использующих старые технологии.
Заключение
Исследованы кооперативные явления в системах взаимодействующих, рыночных предприятий, эволюционирующих естественным образом в условиях рыночной экономики. Рассмотрены регулярный и стохастический типы поведения экономических систем. Обсуждены оптимальные способы управления развитием экономических систем и показаны возможности исключения катастрофических ситуаций.
Рецензенты:
Торопцев Е.Л., д.э.н., профессор, заведующий кафедрой математического анализа, Институт математики и естественных наук, Северо-Кавказский федеральный университет, г. Ставрополь;
Мараховский А.С., д.э.н., профессор кафедры прикладной математики и компьютерной безопасности, Институт информационных технологий и телекоммуникаций, Северо-Кавказский федеральный университет, г. Ставрополь.