Упрощенная схема параллельного резонансного инвертора представлена на рис. 1, а. На схеме показаны паразитные емкости активного элемента (АЭ) (С1) и собственная емкость дросселя (С2), которые должны быть учтены при анализе усилителя на высоких частотах. Для упрощения задачи предположим, что цепь возбуждения, независимо от рабочей частоты, обеспечивает прямоугольную форму управляющих импульсов, а АЭ в открытом состоянии имеет минимальное сопротивление R = 1/Sкр = rнас.
При выполнении этих условий исследуемый усилитель можно представить эквивалентной схемой, показанной на рис. 1, б. Нагрузочный колебательный контур здесь представлен двумя усилителями напряжения
uк = Uкsin(ωt + φ). (1)
Такое представление, разумеется, справедливо лишь для контура с высокой добротностью.
Предположим что сопротивление «ключей» меняется согласно (2) и (3).
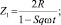 (2)
(2)
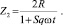 (3)
(3)
Тогда эквивалентную схему усилителя можно описать линейным неоднородным дифференциальным уравнением следующего вида:
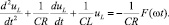 (4)
(4)
где
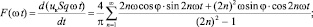 C = 2C0 + C1. (5)
C = 2C0 + C1. (5)
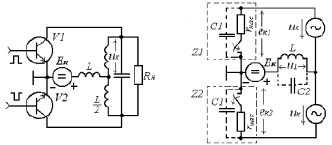
а б
Рис. 1. Параллельный резонансный инвертор и его эквивалентная схема
Решение (4) в установившемся режиме имеет следующий вид:
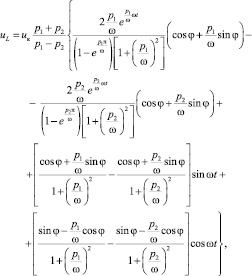 (6)
(6)
где р1, р2 – корни характеристического уравнения (4)
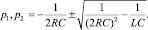 (7)
(7)
В соответствии с эквивалентной схемой, напряжение на Z1
e1 = E – uL – uk. (8)
Энергетические показатели усилителя
Используя (6) и (7), определим постоянную составляющую тока АЭ:
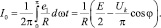 (9)
(9)
При определении переменных составляющих тока АЭ следует учесть, что на повышенных частотах между напряжением возбуждения и первой гармоникой может появиться фазовый сдвиг (φ1), обусловленный искажением формы импульса тока АЭ. В связи с этим будем искать первую гармонику в следующем виде:
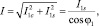 (10)
(10)
где 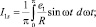
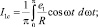
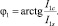
В дальнейшем будем полагать, что в рассматриваемом режиме контур усилителя настроен в резонанс, т.е. φ1 = φ.
Тогда, вычислив интегралы (10), получим
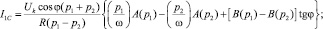 (11)
(11)
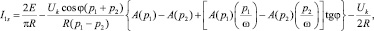 (12)
(12)
где 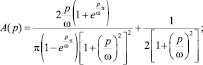
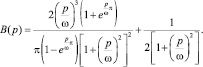 (13)
(13)
При известном сопротивлении нагрузки для одного плеча усилителя (Rн), с помощью (10)–(12), можно определить угол φ, соответствующий работе на настроенную нагрузку:
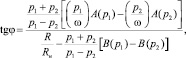 (14)
(14)
и КПД усилителя
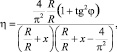 (15)
(15)
где 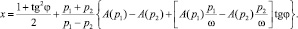 (16)
(16)
Выражения (14), (15), (16) позволяют по известным параметрам схемы усилителя 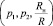 определить КПД на любой частоте. Максимальное значение кпд получается в случае выбора оптимального значения сопротивления нагрузки. К сожалению, исследование (15) на экстремум приводит к сложному трансцендентному уравнению для Rн opt. Сравнительно простые аналитические выражения удается получить лишь в тех случаях, когда
определить КПД на любой частоте. Максимальное значение кпд получается в случае выбора оптимального значения сопротивления нагрузки. К сожалению, исследование (15) на экстремум приводит к сложному трансцендентному уравнению для Rн opt. Сравнительно простые аналитические выражения удается получить лишь в тех случаях, когда 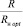 мало и слабо влияет на величину tgφ. В этих случаях можно положить в (14)
мало и слабо влияет на величину tgφ. В этих случаях можно положить в (14) 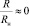 и, следовательно, tgφ и x оказываются независимы от Rн.
и, следовательно, tgφ и x оказываются независимы от Rн.
Исследуя (15) на экстремум, для указанного частотного случая, найдем
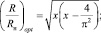 (17)
(17)
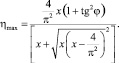 (18)
(18)
Практически выражения (17) и (18) можно использовать для p1 > –1,5 и p2 < –5,0. Однако для детального исследования частотной зависимости к.п.д. усилителя приходится анализировать режимы работы с большими фазовыми сдвигами (φ > 15°). В этом случае необходимо пользоваться точными соотношениями (14)–(16) и численными методами решения уравнений.
Построены кривые равных уровней КПД при оптимальной величине Rн, которые представлены на рис. 2.
Таким образом, КПД инвертора можно представить некоторой поверхностью. Сечения этой поверхности плоскостями, проходящими через начало координат и ось, перпендикулярную к плоскости рисунка, образуют семейство частотных характеристик
η = fn(ω). (19)
Действительно, каждой секущей плоскости соответствует определенное отношение 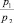 (или, иначе, определенные значения R, L, C1, C2), поэтому положение точки исследуемой поверхности, лежащей в секущей плоскости, полностью определяется частотой усилителя.
(или, иначе, определенные значения R, L, C1, C2), поэтому положение точки исследуемой поверхности, лежащей в секущей плоскости, полностью определяется частотой усилителя.
Приведен ряд частотных характеристик для некоторых значений отношения 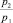 представленных на рис. 3.
представленных на рис. 3.
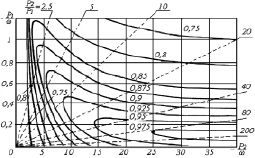
Рис. 2. Номограмма для определения кпд инвертора при оптимальном значении сопротивления нагрузки
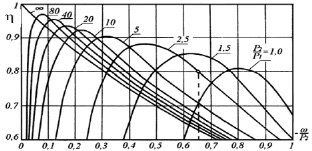
Рис. 3. Зависимости КПД инвертора от частоты
Анализируя полученные характеристики, можно сделать следующие выводы:
1. Для повышения рабочей частоты инвертора необходимо уменьшать отношение 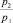 , что в первом приближении эквивалентно уменьшению индуктивности дросселя
, что в первом приближении эквивалентно уменьшению индуктивности дросселя 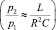 . Однако при этом следует иметь в виду, что одновременно сокращается относительная полоса частот эффективных режимов усилителя. В результате инверторный режим усилителя при работе на высоких частотах в какой-то степени подобен бигармоническому режиму [4].
. Однако при этом следует иметь в виду, что одновременно сокращается относительная полоса частот эффективных режимов усилителя. В результате инверторный режим усилителя при работе на высоких частотах в какой-то степени подобен бигармоническому режиму [4].
2. Перемещение рабочего диапазона в область высоких частот приводит к уменьшению максимума частотной зависимости КПД.
Чтобы найти предельную частоту эффективной работы инвертора, необходимо задать: во-первых, коэффициент перекрытия диапазона частот (σ), в пределах которого эффективность усилителя не падает ниже определенной величины; во-вторых, минимальное значение кпд, которое должно быть обеспечено в пределах установленного диапазона. В дальнейшем для определенности принимается σ = 2; ηmin = 0,8.
Обращаясь к частотным характеристикам, теперь нетрудно установить, что заданным условиям удовлетворяет характеристика, для которой
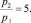 (20)
(20)
По выбранной характеристике можно определить максимальную частоту эффективной работы усилителя
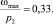 (21)
(21)
Выражения (20) и (21) позволяют непосредственно связать ωmax с параметрами схемы. Для этого достаточно воспользоваться соотношениями (7)
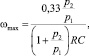 (22)
(22)
или с учетом (20)
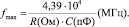 (23)
(23)
Из полученного выражения, на первый взгляд, следует, что fmax не зависит от индуктивности дросселя. В действительности величина индуктивности дросселя должна быть вполне определенной, так как в противном случае не будут обеспечены исходные значения γ и ηmin. Необходимая индуктивность дросселя может быть найдена с помощью (7), (20) и (21):
L = 7,2R2C. (24)
По существу, индуктивность дросселя входит в постоянный коэффициент выражения (23), который остается постоянным только при выборе L в соответствии с (24).
Заметим, что максимальная частота в (23), в сущности, отражает лишь потенциальные возможности параллельного инвертора. Реализовать эти возможности на практике, по-видимому, будет трудно, так как с ростом рабочей частоты усилителя задача формирования напряжения возбуждения прямоугольной формы существенно усложняется. Кроме того, при использовании колебательной системы с низкой добротностью в нагруженном состоянии существенное влияние на величину кпд инвертора могут оказать высшие гармоники. Наконец, не всегда могут быть практически осуществимы оптимальные значения эквивалентного сопротивления нагрузки (Rн opt).
Выводы
1. При оптимальном выборе параметров нагрузочной цепи существенно расширяется полоса рабочих частот без перестройки колебательной системы.
2. Пиковое напряжение на коллекторе будет превышать примерно в 3,5 раза напряжение источника питания.
3. Параллельный резонансный инвертор способен работать на частотах на порядок выше, чем последовательный резонансный инвертор [1].
4. Перемещение рабочего диапазона в область высоких частот приводит к уменьшению максимума частотной зависимости КПД.
Рецензенты:
Пальчун Ю.А., д.т.н., профессор, ученый секретарь, Сибирский государственный научно-исследовательский ордена Трудового Красного Знамени институт метрологии, г. Новосибирск;
Сединин В.И., д.т.н., профессор, заведующий кафедрой «Системы автоматизированного проектирования», ФГБОУ ВПО «Сибирский государственный университет телекоммуникаций и информатики», г. Новосибирск.



