В настоящее время актуальной проблемой является получение изделий сложной геометрии из полимерных композиционных материалов, армированных коротким волокном.
При инжекционном литье (ИЛ) таких материалов, которые, как правило, обладают низкой текучестью, возможно появление таких характерных дефектов, как недолив, коробление, высокая усадка, линии стыка.
С целью оптимизации конструкторско-технологических параметров ИЛ деталей сложной геометрии (расположения и геометрии литников, температуры подаваемого расплава и пресс-формы и другие) для предотвращения указанных выше дефектов производят имитационное моделирование ИЛ методами численного анализа.
Процесс заполнения формообразующих полостей пресс-формы формализуется решением краевой задачи численными МКЭ-методами на основе уравнения Навье – Стокса. Система состоит из двух уравнений: уравнения движения и уравнения неразрывности. В векторном виде для несжимаемой жидкости они записываются следующим образом:
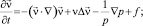 (1)
(1)
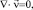 (2)
(2)
где ∇ – оператор Гамильтона; Δ – оператор Лапласа; t – время; ν – коэффициент кинематической вязкости; ρ – плотность; p – давление, 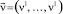 – векторное поле скоростей;
– векторное поле скоростей; 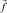 – векторное поле массовых сил. Неизвестные p и
– векторное поле массовых сил. Неизвестные p и  являются функциями времени t и координаты x ∈ Ω, где Ω ∈ n, n = 2, 3 – плоская или трёхмерная область, в которой движется жидкость.
являются функциями времени t и координаты x ∈ Ω, где Ω ∈ n, n = 2, 3 – плоская или трёхмерная область, в которой движется жидкость.
Вязкость расплава обычно определяют по модели Кросса – Вильямса – Ландела – Ферри (Cross-WLF), которая описывает зависимость вязкости от температуры, скорости сдвига и давления.
Данная модель определяется следующим уравнением:
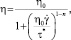 (3)
(3)
где η – вязкость расплава (Па·с); η0 – вязкость при нулевом сдвиге, или «ньютоновский предел», к которому стремится вязкость при очень низких скоростях сдвига;  – скорость сдвига (1/c); τ* – критический уровень напряжения в начале сдвиговой деформации, который определяется путем подгонки кривой.
– скорость сдвига (1/c); τ* – критический уровень напряжения в начале сдвиговой деформации, который определяется путем подгонки кривой.
Вязкость при нулевом сдвиге определяется по формуле
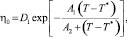 (4)
(4)
где T – температура (K); T* – температура стеклования, определённая подгонкой кривой; А2 – коэффициент, равный A3 + D3p; p – давление (Па); D1, A1, A3 и D3 – коэффициенты, полученные из экспериментальных данных.
Для вычисления температуры стеклования используется следующее выражение:
T* = D2 + D3p, (5)
где D2 – коэффициент, полученный из экспериментальных данных.
К наиболее известным системам относятся Moldex3D и Moldflow. Результаты CAE-моделирования, которые носят дискретный характер, для поиска оптимального решения обычно аппроксимируются регрессионными зависимостями.
В работе Y.F. Yin [5] посредством моделирования процесса инжекционного литья было определено оптимальное положение литника и время заполнения формы, а также на основе данных об усадке определена оптимальная температура впрыска. С использованием данных анализа была разработана регрессионная модель для определения математической зависимости между объёмной усадкой и параметрами процесса (температурой пресс-формы, температурой расплава, давлением и временем впрыска, временем охлаждения).
Авторы Y. Wang, H. Wang, X. Xu, X. Zhang [4] объектом моделирования выбрали рабочее колесо насоса. Были предложены разные варианты расположения литниковых каналов и посредством CAE-системы изучено влияние на давление заполнение полости, распределение линий спая и объёмной усадки.
C. Fetecau, I. Postolache, F. Stan [3] для большего понимания процесса инжекционного литья на основе экспериментальных данных была создана компьютерная модель. Для оптимизации процесса было исследовано влияние геометрии литниковой системы на фазы заполнения и уплотнения.
B.H. Min [1] были проведены натурные эксперименты, по данным которых построена регрессионная модель зависимости усадки от скорости впрыска и давления выдержки. Оптимальные параметры найдены с помощью метода градиентного спуска.
Автором B.H.M. Sadeghi [2] для предсказания качества изделия, получаемого методом инжекционного литья, на основе ключевых параметров процесса разработана нейронная сеть.
Численное моделирование
Основным критерием качества изделий, изготовляемых методом литья под давлением, является полное заполнение формообразующей полости пресс-формы. Наряду с требованием по полному заполнению формообразующей полости, для армированных ПКМ возникает требование к равномерному распределению и направленности упрочняющего волокна. Выполнение данных требований должно обеспечиваться выбором таких параметров технологического процесса переработки материала, как скорость и давление впрыска расплава, его температура. Поиск указанных параметров является целью численного моделирования.
Объект моделирования – статорная лопатка компрессора ГТД. Полимерный композиционный материал – полиэфиэфиркетон, на 40 % армированный углеволокном (PEEK90HMF40).
Коэффициенты модели вязкости Cross-WLF приведены в таблице.
Основные этапы моделирования приведены на схеме (рис. 1).
Коэффициенты модели вязкости для PEEK90HMF40 по зависимости (4)
|
Коэффициент |
n |
τ, Па |
D1, Па·с |
D2, K |
D3, K/Па |
A1 |
A2, K |
|
Значение |
0,17 |
905300 |
2,02865·108 |
417,15 |
0 |
18,082 |
51,6 |
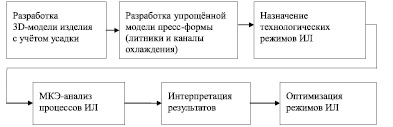
Рис. 1. Этапы моделирования инжекционного литья (ИЛ)
К особенностям моделирования следует отнести следующие моменты:
1. Литниковая система и формообразующая полость формируется поверхностью готового изделия, а не пресс-формы.
2. Расчётная модель пресс-формы упрощается, она задается указанием габаритных размеров, литниковых каналов и каналов охлаждения.
3. Граничными условиями являются технологические параметры процесса.
На основе 3D-модели изделия строится сетка конечных элементов. В целом для прогнозирования распределения давления не обязательна высокая плотность сетки. Но точное представление общей картины заполнения может быть получено, только если сетка детализирована достаточно, чтобы отразить все подробности детали. При недостаточно качественной сетке при расчёте могут не проявиться следующие дефекты: «эффект задержки», воздушные «ловушки», линии спая (стыка).
Для предварительного расчёта в нашем случае была использована сетка с относительно крупными элементами размером 2 мм, что привело к ошибкам генерации сетки на поверхностях с радиусами локальной кривизной меньше указанного размера. Это – тонкие кромки пера лопатки. Добавление новых элементов или разбивка области на более мелкие элементы удобнее производится в препроцессорах специализированных программных продуктов, например ANSYS.
На следующем этапе выбирается расположение литника и каналов охлаждения. Входной литник расположен со стороны нижней полки с целью её максимально быстрого полного заполнения для исключения возникновения зон непролива.
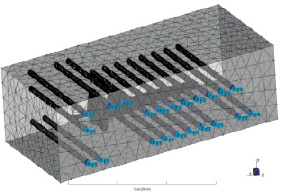
Рис. 2. Расчётная КЭ-модель пресс-формы
Температура расплава, а следовательно, его текучесть при заполнении формующей полости зависит от тепловых потоков, подводящих и отводящих тепло от расплава. Для достижения необходимой равномерности прогрева в КЭ – модель пресс-формы вводятся каналы подогрева маслом (рис. 2). Температура, объемный расход масла, диаметр и расположения каналов также являются параметрами оптимизации при моделировании.
Обычно каналы подогрева/охлаждения описываются конечными элементами типа «балка».
Для поиска оптимальных параметров ИЛ была построена радиально-базисная нейронная сеть c одним внутренним слоем нейронов, с топологией типа 5:5-4-2:2 (рис. 3).
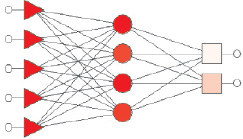
Рис. 3. Топология нейронной сети
Входные параметры: температура расплава, температура пресс-формы, время заполнения, давление заполнения, давление выдержки.
Выходные параметры: процент заполненности формообразующей полости, степень направленности углеволокна в продольном направлении.
Для обучения сети использовались 10 вариаций рекомендуемых производителем материала параметров переработки для общего случая с интервалом варьирования 20 % от номинального значения, например номинальная температура подаваемого расплава – 370 °С, а температура пресс-формы – 230 °С, время заполнения – 10 с.
Обсуждение результатов моделирования
В результате расчёта на номинальных режимах получена картина заполнения материалом формообразующей оснастки, степень коробления, распределение температуры в оснастке и в детали в процессе литья, а также распределение армирующего волокна, наиболее вероятное при заданных технологических параметрах литья.
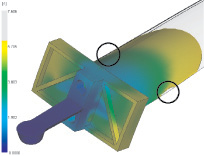
Расчёт показал область непролива в области пера (рис. 4). Эта незаполненная область возникла вследствие недостаточного давления во время заполнения нижней полки. Когда полка полностью заполняется, давление и, соответственно, скорость потока в области пера резко увеличивается, но часть расплава всё равно успевает застыть.
 а
а 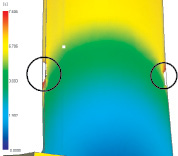 б
б
Рис. 4. Образование зоны непролива: а – расположение зон непролива; б – динамика заполнения формы вблизи зон непролива
 а
а  б
б
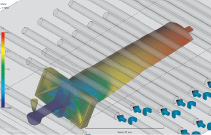
Рис. 5. Время заполнения (a) и степень ориентированности наполнителя вдоль пера лопатки (б)
Оптимизация процесса инжекционного литья
На основе нейронной сети были получены режимы литья, которые обеспечили наилучшую заполняемость формы при максимальной величине тензора ориентации армирующего волокна. Оптимизированные режимы были верифицированы численным моделированием.
Установлено, что непролив уменьшается при увеличении скорости впрыска (т.е. уменьшении времени впрыска). Проведённые расчёты в диапазоне времени впрыска 4–7 с обеспечили процент заполнения 99,97–100 %.
В итоге в качестве оптимальных параметров литья выбраны: время впрыска 4 с, а температура охлаждения расплава – 170 °С. Результаты расчёта с данными параметрами представлены на рис. 5.
Степень ориентации вдоль пера лопатки (ось Z) показана на рис. 5. Чем выше значение, тем больше волокон ориентации вдоль оси Z. В данном направлении в области пера лопатки ориентировано 75–90 % наполнителя (углеволокна), что является довольно высоким показателем.
Выводы
1. Апробирована методика оптимизации технологических параметров инжекционного литья изделий сложной геометрии из коротковолокнистых полимерных композиционных материалов (статорная лопатка ГТД). Методика основана на анализе численного моделирования процесса заполнения и ориентации армирующего волокна методом конечных элементов с последующим поиском области рациональных режимов литья с применением 3-слойной радиально-базисной нейронной сети.
2. Установлено, что требуемая ориентация углеволокна (максимальное значение тензора ориентации) в наибольшей степени зависит от скорости впрыска расплава, которая для минимальной температуры пресс-формы, обеспечивающей полное заполнение формы, должна быть максимальной.
Рецензенты:
Дровянников В.И., д.э.н., проректор по учебной и воспитательной работе, ЧОУ ВО «Международный институт рынка», г. Самара;
Макаров А.А., д.т.н., профессор кафедры информационных систем и компьютерных технологий, ЧОУ ВО «Международный институт рынка», г. Самара.



