В данной работе изложена разработанная авторами методика решения комплексной задачи по оценке прочности и долговечности стальных оболочек вращения с учетом необратимых деформаций, повреждаемости материалов вследствие ползучести и высокотемпературной водородной коррозии [1, 2, 4, 5]. Эта задача решалась в термовязкоупругопластической постановке, с применением соотношений теории неизотермических процессов упругопластического деформирования элементов твердого тела по траекториям малой кривизны, линеаризованных методом дополнительных деформаций. Учет влияния повреждаемости материалов вследствие ползучести на процесс ее деформирования осуществляется путем введения параметра повреждаемости в соотношения термовязкопластичности, для определения которого используется хорошо зарекомендовавшее себя кинетическое уравнение повреждаемости в форме, предложенной Ю.Н. Работновым.
Коррозионное воздействие водорода на стали в настоящее время изучено достаточно хорошо, и на эту тему имеется множество публикаций, в которых показано, что влияние водорода существенным образом сказывается на изменении вида диаграммы деформирования углеродистых сталей, при этом снижаются прочностные и пластические свойства сталей и происходит их охрупчивание, ухудшаются длительные прочностные характеристики сталей. Вместе с тем возможность комплексного учета повреждаемости материалов вследствие температурной ползучести и водородной коррозии почти нигде не рассмотрена. Таким образом, основной и наиболее сложной задачей исследования является определение условий перехода механических характеристик сталей из исходного состояния в обезуглероженное. Для этого используются несколько подходов, подробно изложенных авторами в публикации [3]. Рассмотрим некоторые из них.
Обобщенная модель химического взаимодействия
Предполагается, что влияние водорода, контактирующего с материалом конструкций, проявляется по истечении определенного времени, называемого инкубационным периодом tинк. После завершения инкубационного периода начинается интенсивное обезуглероживание материала конструкции, сопровождающееся ухудшением его механических свойств. При этом механические свойства материалов могут существенно изменяться. Этот период называется периодом активных химических превращений tкр. По завершении указанного периода дальнейших изменений механических свойств сталей под воздействием водорода не происходит.
Влияние водорода на свойства материала в данной модели представляется в виде дифференциального уравнения для параметра химического взаимодействия водорода с материалом конструкции µ, изменяющегося от m0 до mкр, принадлежащего интервалу (0; 1) и характеризующего степень поражения материала вследствие водородной коррозии [3]:
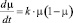 (1)
(1)
с условиями:
t = 0, μ = μ0(p, T, ωС);
t = tинк, μ = μп(p, T, ωС); (2)
t = tкр, μ = μкр(p, T, ωС).
Здесь k(p, T, ωС) – коэффициент, учитывающий влияние давления p, температуры T и степени поврежденности ωС на кинетику химических превращений, приводящих к деградации физико-механических свойств материала.
Решение уравнения (1) имеет вид [3] (кривая 1 на рис. 1):
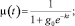 (3)
(3)
g0 = (1 – μ0)/μ0; (4)
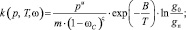 (5)
(5)
gп = (1 – μп)/μп, (6)
где m, u, B, z – константы, экспериментально определяемые для различных марок стали. Значения μ0, μп и μкр определяются по методике, изложенной в работе [3] и связаны с анализом кинетики выделения метана при взаимодействии водорода с углеродом, содержащимся в материале стенки.
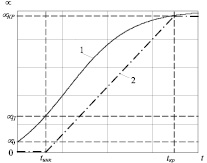
Рис. 1
При этом учет влияния уровня напряжений на длительность инкубационного периода и скорость высокотемпературной коррозии вводится зависимость коэффициента m от σ в виде
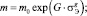
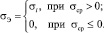 (7)
(7)
Здесь: m0, G, g – константы материала; σэ – эквивалентное напряжение; σi – интенсивность нормальных напряжений, σср – среднее напряжение.
Распределение давления по толщине оболочки вычисляется [3]:
для плоской стенки:
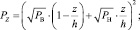 (8)
(8)
для оболочки:
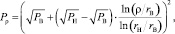 (9)
(9)
где z – плоская координата; ρ – сферическая координата; h – толщина оболочки; rВ – внутренний радиус оболочки; rН – наружный радиус оболочки; PВ – внутреннее давление; PН – наружное давление.
Упрощенная модель химического взаимодействия
Так как t < tинк изменений механических свойств материалов еще не происходит, а при t > tкр уже не происходит [3], то логистическую кривую Ферхюльста можно аппроксимировать трехзвенной линией (на рис. 1 линия 2) и конкретизировать в виде
μ(t) = a t + μп, (10)
где
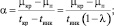 (11)
(11)
μп ≤ m(t) ≤ μкр. (12)
Длительность инкубационного периода, как показано в работе [3], определяется с помощью следующего соотношения:
tинк = m p–u·exp(B/T), (13)
где p – парциальное давление водорода, МПа; T – температура; m, u, B – некоторые константы, экспериментально определяемые для различных марок стали.
Длительность периода активных химических превращений определяем следующим образом [3]:
tкр = λ tинк, (14)
где λ – параметр, являющийся мерой скорости химического взаимодействия водорода с конструкцией, показывающий, во сколько раз время до завершения периода изменений механических свойств материала отличается от продолжительности инкубационного периода, т.е. λ = tкр/tинк. Для стали 20 этот параметр принимает значения в пределах от 5 до 10 [3].
В том случае, если известно, что процесс обезуглероживания конструкции значительно короче времени до начала разрушения, можно использовать еще более простые модели воздействия водородосодержащей среды. В частности, замену логистической кривой, описывающей плавное изменение механических характеристик, на ступенчатое их изменение от начального до конечного состояния, по прошествии либо инкубационного периода, либо периода активных химических превращений.
На рис. 2 схематически показан примерный характер изменения временного сопротивления стали 20 вследствие воздействия водорода. Здесь σв и 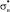 – соответственно значения временного сопротивления материала в исходном и обезуглероженном состоянии. Другие механические характеристики материала (E, σт, δ, ψ) изменяются в процессе обезуглероживания аналогичным образом [3].
– соответственно значения временного сопротивления материала в исходном и обезуглероженном состоянии. Другие механические характеристики материала (E, σт, δ, ψ) изменяются в процессе обезуглероживания аналогичным образом [3].
При использовании варианта 1 считается, что механические характеристики ступенчато изменяются по истечении периода времени, соответствующего tкр, а в варианте 2 это изменение происходит сразу же после завершения инкубационного периода, то есть при tкр = tинк. При этом вариант 1 дает завышенную оценку времени обезуглероживания, а вариант 2 – заниженную. Кроме того, в варианте 2 не требуется нахождение параметра λ .
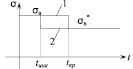
Рис. 2
Учет влияния напряжений на скорость коррозии и распределение давлений осуществляется так же, как и в обобщенной модели.
На основе упрощенной модели химического взаимодействия построена также модель оценки кинетики движения фронта обезуглероживания, целью разработки которой была возможность использования при аналитических расчетах, однако она может использоваться только для некоторых несложных моделей пластин и неспособна учитывать нестационарный характер изменения тепловых, силовых нагрузок и давления водорода, а также влияние уровня напряжений на скорость движения фронта обезуглероживания.
В действительности моделей воздействия водородосодержащей среды значительно больше, наиболее распространенные из них подробно рассмотрены в работе [3]. Здесь же приведены только те модели, которые могут использоваться в составе разработанного авторами программного комплекса по расчету напряженно-деформированного состояния оболочечных конструкций [1, 2, 4, 5].
Технически учет влияния водорода на прочностные свойства конструкции реализован следующим образом. Для каждого из материалов конструкции введены механические характеристики двух его состояний – исходного и обезуглероженного. Если процесс обезуглероживания отсутствует (инкубационный период не завершен), то для расчета параметров напряженно-деформированного состояния берутся исходные механические характеристики материала. Если в материале уже происходит процесс обезуглероживания, но он еще полностью не завершен, то значения механических характеристик материала на этой стадии расчета, вычисляются путем линейной интерполяции в зависимости от текущего значения m(t) между исходным и обезуглероженным состояниями. Если процесс обезуглероживания завершен, то для расчета берутся характеристики обезуглероженного материала.
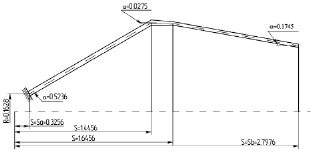
Рис. 3
С применением данной методики были проведены расчеты составной двухслойной конической оболочки, осевое сечение которой приведено на рис. 3. Исследуемая конструкция состоит из трех участков. По форме меридиана координатной поверхности все три участка оболочки являются коническими. Левый торец оболочки жестко заделан, правый свободен. Толщина первого участка 40 мм (конусность 30°), третьего – 30 мм (конусность 10°). Второй участок является переходным (конусность 1,575°). Давление водорода осуществляется с внутренней стороны и постоянно во времени.
Внутренний слой, обращенный к водородосодержащей среде, изготовлен из материала 12Х18Н9Т, а внешний – из материала сталь 20.
Давление водорода принималось равным 2, 2,5 и 3 МПа. Выбор значений обусловлен следующими соображениями: при 2 МПа в материале имеют место только мгновенные упругие деформации и деформации ползучести, а при 2,5 и 3 МПа – еще и мгновенные пластические. Все расчеты приведены для температуры 500 °С.
Константы материала в соотношениях были взяты из [3], которые для стали 20 при данных условиях нагружения принимают следующие значения: k = 1,49·10–5 (МПа)·u, ч; u = 1,73; B = 13500; λ = 1…10. Согласно данным, приведенным в работе [3], механические сплавы 12Х18Н9Т под воздействием водорода практически не изменяются.
Влияние уровня напряжений на скорость процесса обезуглероживания в данном расчете не учитывалось, поскольку для этого требуются дополнительные исследования.
В работе исследовалось влияние толщины защитного слоя 12Х18Н9Т на длительную прочность оболочки, а также распределение, меридиональных напряжений, деформаций зон пластичности и повреждаемости в моменты времени до разрушения, перед разрушением и непосредственно после него. Некоторые результаты приведены на рис. 4–6.
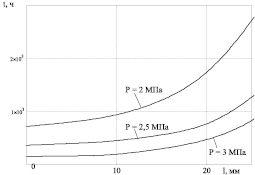
Рис. 4
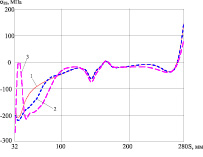 а
а 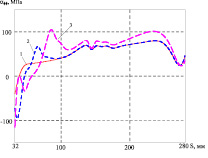 б
б
Рис. 5
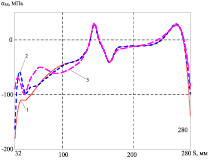 а
а 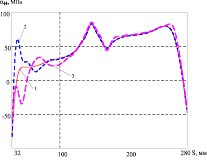 б
б
Рис. 6
На рис. 4 приведены графики, показывающие время до разрушения оболочки в зависимости от толщины защитного слоя при разных давлениях. Введение защитного слоя существенно увеличивает время до разрушения оболочки. Набор таких графиков, полученных при разных давлениях и температурах, позволяет подобрать требуемую толщину защитного слоя при заданном ресурсе изделия.
На рис. 5 приведены кривые, показывающие распределение меридиональных (а) и окружных (б) напряжений на внутренней поверхности, а на рис. 6 – на внешней поверхности для толщины защитного слоя 5 мм и давления 2,5 МПа. Кривая 1 соответствует началу процесса нагружения, кривая 2 – моменту времени t = 379 ч (непосредственно перед разрушением), кривая 3 – моменту времени t = 380 ч (сразу после начала разрушения). На этих графиках видно перераспределение напряжений по мере развития пластических деформаций и накопления повреждений от наружного слоя к более прочному внутреннему. Однако по мере накопления повреждений во внутреннем слое происходит вторичное перераспределение напряжений уже к наружному слою. При этом наиболее нагруженными точками оболочки являются точки внутренней поверхности. Начало процесса разрушения происходит в точке внутренней поверхности с меридиональной координатой S = 0,457 м.
Таким образом, исследуя историю изменения напряженно-деформированного состояния с учетом перемещения фронта обезуглероживания и повреждаемости материалов при ползучести и используя соответствующие критерии мгновенной и длительной прочности, можно оценить ее несущую способность и долговечность с учетом воздействия всех вышеназванных факторов.
Рецензенты:
Богомолов А.Н., д.т.н., профессор, проректор по научной работе, ФГБОУ ВПО «Волгоградский государственный архитектурно-строительный университет», г. Волгоград;
Богданов Е.П., д.т.н., профессор кафедры «Информационные системы и технологии», ФГБОУ ВПО «Волгоградский государственный аграрный университет», г. Волгоград.



