Одним из наиболее прогрессивных видов транспорта, обеспечивающим высокую производительность и технико-экономическую эффективность при больших грузопотоках, является конвейер. Анализ представленных в работе [5] конструкций существующих конвейеров показывает, что на горных предприятиях для транспортирования насыпных грузов с различным гранулометрическим составом (уголь, руда и т.д.) на расстояния от 20 до 100 м целесообразно использовать инерционные конвейеры с постоянным давлением груза на дно желоба. Инерционные конвейеры, как машины, относящиеся к динамическим колебательным системам, обладают высокой степенью стабильности в связи с тем, что амплитуда колебаний желоба в процессе работы конвейера постоянна. За последние десятилетия появились схемы инерционных конвейеров с изменяемыми рабочими параметрами, для которых высокая амплитуда при малой частоте колебаний обеспечивает высокую скорость транспортирования, не вызывая подбрасывания груза. В настоящее время задача оптимального проектирования механизмов конвейера сводится к выбору наиболее совершенной динамической схемы и параметров ее структурных элементов, при которых движения рабочих органов максимально удовлетворяют технологическим требованиям, а условия нагружения элементов машины – конструктивным ограничениям.
Исследования кинематических и динамических параметров инерционных конвейеров проводятся в основном для схем конвейеров с жесткими звеньями [8, 6]. Учитывая, что жесткость тяги, как последнего звена в кинематической цепи привода конвейера, оказывает наибольшее влияние на кинематику движения рабочего органа, исследования привода инерционного конвейера с тягой с переменной жесткости являются актуальными. В предыдущей работе [4] авторами настоящей статьи была выбрана структурная схема (рис. 1, а), позволяющая регулировать скорость перемещения груза за счет использования тяги с переменной жесткостью и достигать максимальной производительности транспортирования сыпучих материалов с различным гранулометрическим составом. В настоящей работе проводились исследования кинематических и динамических параметров движения желоба инерционного конвейера для транспортировки горных пород с учетом влияния жесткости тяг. Известно, что точность теоретических исследований зависит от полноты представления физических явлений, от принятых допущений и методов решений, т.е. от построения динамической модели и способов ее реализации. В работе [3] была представлена динамическая модель инерционного конвейера с учетом влияния жесткости тяг на колебания желоба, изображенная на рис. 1, б.
Движение желоба инерционного конвейера, согласно этой динамической схеме, при установившемся режиме движения и сухом трении описывалось дифференциальным уравнением
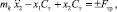 (1)
(1)
где mk – приведенная масса желоба и груза; x1 – координата вращательной кинематической пары С, так как кинематическая цепь ОАВО1С жесткая (рис. 1); x2 – координата приведенной массы колеблющегося желоба с грузом; Cт – жесткость тяги; Fтр – сила сопротивления движению, знакопеременная на рабочем и холостом ходах желоба конвейера.
 а
а 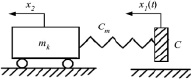 б
б
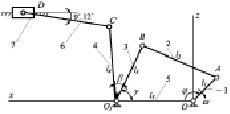
Рис. 1. Схемы привода инерционного конвейера: а – кинематическая схема привода (кривошип 1; шатун 2; коромысло 3–4; тяга 6; желоб конвейера 7); б – динамическая схема привода инерционного конвейера
Учитывая, что приводной двигатель передает мощность через жесткие звенья цепи ОАВО1С (рис. 1), методом векторных контуров был определен закон движения точки С:
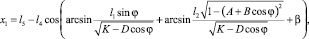 (2)
(2)
где b – угол между звеньями коромысла СО1В; φ – обобщенная координата кривошипа ОА; φ = ωt; ω – угловая скорость кривошипа; А, В, К, D – величины, определяемые геометрическими параметрами конструкции:
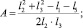
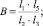
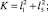
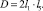
Для решения уравнения (1) был применен кусочно-линейный метод, так как системы, движение которых рассматривается с учетом сухого трения, относятся к нелинейным. Уравнение движения желоба с грузом представляли в виде суммы свободных и вынужденных колебаний с учетом действующей на желоб силы трения Fтр. Знакопеременную скорость желоба выражали единичной функцией 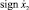 . В соответствии с этим свободные колебания желоба описываются уравнением:
. В соответствии с этим свободные колебания желоба описываются уравнением:
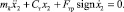 (3)
(3)
Анализ свободных колебаний желоба проводился методом поэтапного рассмотрения, при этом последовательно выделялись интервалы движения желоба с постоянным знаком скорости [2]. На первом этапе желоб из крайнего правого положения (х2 = А1), движется влево без начальной скорости под действием силы упругости тяги, его скорость 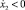 , а уравнение движения желоба
, а уравнение движения желоба
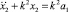 (4)
(4)
где k – частота свободных колебаний, 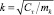 ; a1 – максимальное отклонение желоба влево под действием силы трения,
; a1 – максимальное отклонение желоба влево под действием силы трения, 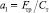 .
.
Уравнение (4) справедливо при А1 > a1, так как при отклонении желоба на величину А1 ≤ a1 силы упругости тяги недостаточно для преодоления силы трения. Область положений желоба –a1 < х2 <+a1 является «зоной застоя». Общим решением уравнения (4) будет выражение
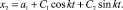
После определения постоянных С1 и С2 из начальных условий движения желоба x0 = A1; 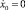 оно примет вид
оно примет вид
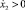
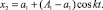 (5)
(5)
Закон движения желоба (5) справедлив до момента времени t1 = π/k, пока скорость желоба отрицательна, так как
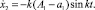
В этот момент желоб остановится, а его смещение в левую крайнюю точку будет равно x2 = –(A1 – 2a1). После остановки желоб начнет двигаться вправо.
На втором этапе движения, когда, уравнение движения
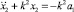 (6)
(6)
может рассматриваться как уравнение гармонических колебаний со смещением (x2 + a1). Это движение также происходит в течение времени π/k. Максимальное отклонение вправо на втором цикле колебания x2 = A1 – 4a1. Процесс движения продолжается до тех пор, пока желоб не попадет в зону застоя и не остановится. Фазовый портрет свободных колебаний желоба с грузом, как системы с сухим трением представлен на рис. 2.
В координатах (х2, 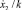 ) гармонический закон движения желоба изображается дугами окружности. На первом этапе, когда
) гармонический закон движения желоба изображается дугами окружности. На первом этапе, когда 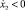 , движение изображается полуокружностью радиусом (A1 – a1) с центром в точке (x2 = a1). Второй этап движения (при
, движение изображается полуокружностью радиусом (A1 – a1) с центром в точке (x2 = a1). Второй этап движения (при 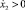 ) представляет собой полуокружность с центром в точке (x2 = –a1). И так до тех пор, пока кривая на фазовой плоскости при
) представляет собой полуокружность с центром в точке (x2 = –a1). И так до тех пор, пока кривая на фазовой плоскости при 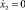 не попадает в зону застоя.
не попадает в зону застоя.
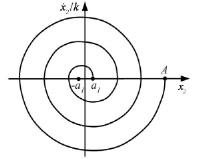
Рис. 2. Фазовый портрет свободных колебаний желоба
Вынужденные колебания желоба возникают при условии, что амплитуда возмущающей силы достаточно велика по сравнению с силой трения Fтр. При этом возмущающая сила выражается функцией Cтx1, изменяющейся по гармоническому закону. Тогда закон вынужденных колебаний желоба описывается уравнением
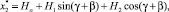 (7)
(7)
а скорость и ускорение желоба конвейера определяются выражениями
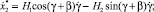 (8)
(8)
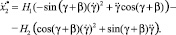 (9)
(9)
В результате определения констант интегрирования Н0, Н1, Н2 из начальных условий движения желоба с учетом дифференциального уравнения (1) был получен закон движения желоба конвейера с учетом жесткости тяг:
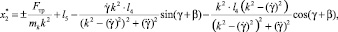 (10)
(10)
где 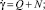
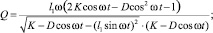 (11)
(11)
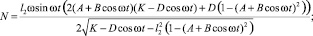 (12)
(12)
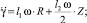 (13)
(13)
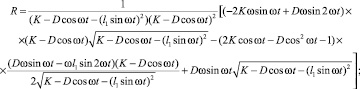 (14)
(14)
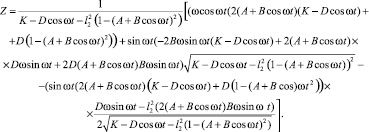 (15)
(15)
При движении желоба с грузом свободные колебания, определяемые уравнением (5), накладываются на вынужденные колебания (10). Наличие сухого трения не изменяет частоту свободных колебаний, так как она во много раз больше частоты вынужденных колебаний, которые и оказывают основное влияние на закон движения желоба конвейера.
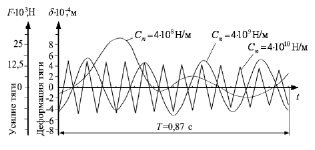
По полученным выражениям (7)–(15) проведены расчеты динамических параметров инерционного конвейера при различной жесткости тяги и построены диаграммы, представленные на рис. 3, а. В расчетах за деформацию тяги принимали величину δ = х2 – х1, а усилия, действующие на тягу F = Cтδ.. Из рис. 3, а видно, что тяга работает на сжатие и на растяжение, т.к. угол между осью тяги и направлением хода желоба невелик и составляет 9…12° (рис. 1, а). При больших углах тяга начинает работать в сложном напряженном состоянии (изгиб – растяжение – сжатие). Наибольшее усилие, действующее на тягу, и ее наибольшая деформация приходятся на начало прямого хода, что соответствует четверти периода Т полного оборота кривошипа ОА. Расчеты также показали, что на инерционном конвейере можно устанавливать тягу c жесткостью 4∙107 ≤ Ст ≤ 4∙109. Для большей жесткости закон движения не отражает действительного колебательного процесса.
Результаты кинематических расчетов движения желоба и груза для инерционного конвейера с тягами различной жесткости представлены на рис. 3, б.
а
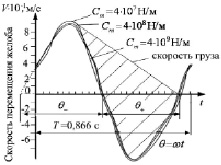
б
Рис. 3. Результаты динамических и кинематических расчетов: а – диаграммы деформаций тяги и усилий, действующих на тягу с различной жесткостью; б – диаграмма скорости желоба инерционного конвейера и груза
Процесс взаимодействия груза и желоба на одном цикле движения состоит в том, что на первом этапе груз перемещается вместе с желобом, удерживаясь на нем силой трения покоя. Когда желоб начинает торможение и сила трения не может удержать груз от проскальзывания по желобу, то скорость груза становится больше скорости желоба. Далее, под действием силы трения скольжения, скорости груза и желоба постепенно сближаются, груз перестает скользить по желобу, и параметры его движения опять совпадают с параметрами движения желоба. Результатом этого взаимодействия является положительное перемещение груза при возвращении желоба в исходное положение [7]. Данные, полученные в настоящей работе (рис. 3, б), подтверждают это описание. На диаграмме скорость груза показана для инерционного конвейера с тягой, имеющей жесткость Ст = 4∙107. Заштрихованная область соответствует абсолютному перемещению груза за один цикл работы инерционного конвейера [1]. Видно, что с уменьшением жесткости тяги увеличивается максимальная скорость желоба на рабочем ходу, а следовательно, и скорость перемещения груза по желобу конвейера.
По результатам проведенных исследований можно сделать следующие выводы:
1. Получено дифференциальное уравнение движения желоба инерционного конвейера с тягой переменной жесткости, позволяющее производить анализ движения груза в зависимости от конструкций приводных звеньев, их взаимного геометрического расположения и динамических характеристик.
2. Разработан алгоритм решения дифференциального уравнения и выполнены расчеты движения одномассной системы с переменной жесткостью. Проведен анализ свободных и вынужденных колебаний желоба инерционного конвейера с тягой переменной жесткости.
3. Результаты теоретических исследований инерционного конвейера с гибкой тягой могут быть использованы для выбора оптимальных параметров при создании инерционного конвейера принципиально нового устройства с продольным приложением возмущающего усилия, характеризующегося компактностью, пониженной материалоемкостью и энергоемкостью.



