В настоящее время в вычислительных системах обширное распределение получил целый ряд способов обеспечения отказоустойчивости. Невзирая на их разнообразие, данные способы можно разделить на три основные группы, которые в своей основе используют различные виды избыточности: аппаратную, временную и алгоритмическую, основанную на корректирующих кодах. Обеспечение отказоустойчивости специализированных процессоров цифровой обработки сигналов (ЦОС) состоит в том, чтобы гарантировать непрерывность функционирования за счет тестирования, реконфигурации и перезапуска.
Существуют два подхода к обеспечению отказоустойчивости: аппаратный и алгоритмический. Аппаратный подход основан либо на реконфигурации и исключении из работы отказавших процессоров, либо резервировании. Алгоритмические подходы к обеспечению отказоустойчивости основаны на избыточном кодировании данных и позволяют восстановить правильный результат при возникновении сбоев и отказе процессорного элемента. Этот подход позволяет строить вычислительные структуры с амортизацией отказов.
Рассмотрим функционирование цифрового фильтра с конечной импульсной характеристикой, отклик которого задается уравнением
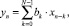(1)
или, иначе,
yn = b0xn + b1xn–1 + b2xn–2 + … + bnxn–N + 1. (2)
Таким образом, для построения систем цифровой фильтрации требуется эффективная реализация соотношения типа дискретной свертки, которая в свою очередь раскладывается на операции взвешенного суммирования задержанных на равные промежутки входного сигнала.
Для конечных последовательностей обычно применяется линейная свертка y(n), которая для двух конечных последовательностей x(n) и h(n) длины N1 и N2 будет содержать N1 + N2 – l отсчетов
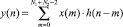, (3)
для отрицательных значений индексов значение h берется равным нулю.
Для описания процессов фильтрации можно применить алгебру полиномов, приняв отсчеты импульсной характеристики h и входного сигнала x соответствующими полиномиальными коэффициентами. Если длину последовательностей принять равной N, то вычисление линейной свертки будет представлять собой произведение полиномов
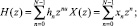
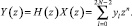(4)
Одним из методов вычисления свертки является применение различных ортогональных преобразований. При этом образы, полученные при ортогональных преобразованиях последовательностей x(m) и h(n), перемножаются, затем осуществляется обратное преобразование. Во многих практических задачах последовательности обрабатываемых данных представляют собой целые числа, в остальных случаях можно этого добиться путем масштабирования.
Пример 1. Пусть требуется вычислить линейную свертку двух последовательностей x = {1, 3, 2} и h = {3, 2, 1}. Полиномы при этом будут представлять собой
X(z) = z2 + 3z + 2
и
H(z) = 3z2 + 2z + 1.
Перемножив X(z) и H(z), получим полином
Y(z) = H(z) X(z) = (z2 + 3z + 2)(3z2 + 2z + 1) = = 3z4 + 11z3 + 13z2 + 7z + 1,
коэффициенты которого равны отсчетам линейной свертки.
В предположение того, что входной сигнал и импульсная характеристика фильтра ограничены и не превышают некоторого простого числа p/2, для вычислений можно применить поля Галуа GF(pn). Если полином P(z) приводим над полем GF(pn) и раскладывается в произведение d неприводимых полиномов Pi(z)
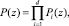(5)
то вычисления можно распараллелить по модулю каждого из полиномов Pi(z), вычислив
Yi(z) = Hi(z) Xi(z) mod Pi(z), (6)
где Hi(z) и Xi(z) вычеты полиномов H(z) и X(z) по модулю Pi(z).
Восстановление результата Y(z) производится на основе Китайской теоремы об остатках (КТО) для системы взаимно простых полиномов Pi(z)
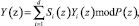(7)
где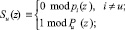 
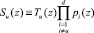– ортогональные базисы,
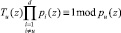– веса базисов.
Вычисления по модулю каждого полинома можно проводить параллельно, это говорит о равноправности остатков. Малоразрядность остатков подразумевает более простую реализацию вычислений, чем при прямом вычислении свертки (3). Если полином P(z) раскладывается на d полиномов первого порядка вида z – α, где α Î GF(p), то вычисления по модулю каждого из таких полиномов сводятся к умножению двух констант по модулю простого p.
Модель вычисления свертки в системе взаимно простых полиномов Pi(z) предполагает:
1. Приведение двух полиномов H(z) и X(z) по модулю pi(z).
2. Умножение вычетов полиномов Hi(z) и Xi(z)по модулю pi(z) (6).
3. Восстановление результата при помощи КТО (7).
Пример 2. Пусть требуется вычислить непериодическую свертку последовательностей x = {1, 3, 1} и h = {2, 0, 1}. Полиномы при этом будут представлять собой X(z) = z2 + 3z + 1 и H(z) = 2z2 + 1. Перемножив X(z) и H(z), получим полином
Y(z) = H(z) X(z) = (z2 + 3z + 1)(2z2 + 1) = 2z4 + 6z3 + 3z2 + 3z + 1,
коэффициенты которого равны отсчетам линейной свертки.
Значения последовательностей не превосходят 3, полиномиальные преобразования можно определить по модулю 7 в поле GF(7). Порядок полинома преобразования должен быть больше 4. Пусть
P(z) = z5 + z4 + z3 + z2 + z + 1,
который в поле GF(76) может быть факторизован
Y(z) = H(z) X(z) = (z + 1) (z + 2) (z + 3) (z + 4) (z + 5).
Воспользуемся описанной ранее методикой для вычисления линейной свертки. Для этого:
Приведем полиномы H(z) и X(z) по модулю pi(z).
Найдем Hi(z) = H(z) mod pi(z):
H1(z) = H(z) mod p1(z) = (2z2 + 1) mod (z + 1) = 3;
H2(z) = H(z) mod p2(z) = (2z2 + 1) mod (z + 2) = 2;
H3(z) = H(z) mod p3(z) = (2z2 + 1) mod (z + 3) = 5;
H4(z) = H(z) mod p4(z) = (2z2 + 1) mod (z + 4) = 5;
H5(z) = H(z) mod p5(z) = (2z2 + 1) mod (z + 5) = 2.
Найдем Xi(z) = X(z) mod Pi(z):
X1(z) = X(z) mod p1(z) = (z2 + 3z + 1) mod (z + 1) = 6;
X2(z) = X(z) mod p2(z) = (z2 + 3z + 1) mod (z + 2) = 6;
X3(z) = X(z) mod p3(z) = (z2 + 3z + 1) mod (z + 3) = 1;
X4(z) = X(z) mod p4(z) = (z2 + 3z + 1) mod (z + 4) = 5;
X5(z) = X(z) mod p5(z) = (z2 + 3z + 1) mod (z + 5) = 4.
Умножим вычеты полиномов Hi(z) и Xi(z) по модулю p
Yi(z) = Hi(z)⋅Xi(z) mod 7:
Y1(z) = H1(z)⋅X1(z) mod 7 = 6⋅3 mod 7 = 4;
Y2(z) = H2(z)⋅X2(z) mod 7 = 6⋅2 mod 7 = 5;
Y3(z) = H3(z)⋅X3(z) mod 7 = 1×5 mod 7 = 5;
Y4(z) = H4(z)⋅X4(z) mod 7 = 5×5 mod 7 = 4;
Y5(z) = H5(z)⋅X5(z) mod 7 = 4⋅2 mod 7 = 1.
Восстановим результаты при помощи КТО. Для этого найдем ортогональные базисы (7):
S1(z) = 5z4 + 5z2 + 5, S2(z) = z4 + 6z3 + 3z2 + 2z + 4,
S3(z) = 2z4 + 3z3 + 2z + 3, S4(z) = z4 + 4z3 + 6z2 + 5z + 2, S5(z) = 5z4 + z3 + 5z + 1.
Обратное преобразование дает
Y(z) = 4(5z4 + 5z2 + 5) + 5(z4 + 6z3 + 3z2 + 2z + 4) + 5(2z4 + 3z3 + 2z + 3) + + 4(z4 + 4z3 + 6z2 + 5z + 2) + 5z4 + z3 + 5z + 1 mod 7 = 2z4 + 6z3 + 3z2 + 3z + 1,
что соответствует ранее вычисленному полиному.
Устройства, функционирующие в полиномиальной системе класса вычетов, обладают следующими достоинствами:
1. Независимость разрядов обуславливает возможность построения автономных вычислительных трактов (каналов) по каждому основанию и позволяет считать последние независимыми элементами.
2. Равноправность разрядов дает возможность изменения функциональных назначений последних, выражающуюся в переводе информационных вычислительных каналов в множество избыточных и наоборот.
3. Использование табличных методов реализации арифметических операций обуславливает малый разброс надежных характеристик вычислительных каналов.
4. Отсутствие межразрядных переносов по основаниям полиномиальной системы классов вычетов.
Из сказанного выше видно, что существующее состояние разработок по теории полиномиальной системы классов вычетов обеспечивает потенциальную возможность повышения не только производительности реализаций арифметических операций, но и информационной надежности вычислительной системы в целом. Поэтому очевидна актуальность разработки алгоритмов построения корректирующих кодов полиномиальной системы классов вычетов. Возможность обнаружения, локализации и коррекции возникающих ошибок возникает благодаря введению информационной избыточности. Введение избыточности в полиномиальный модулярный код осуществляется введением дополнительных контрольных оснований.
Кроме того, полиномиальная система классов вычетов расширенного поля Галуа обладает способностью к варьированию точностью, быстродействием и информационной надежностью в процессе вычисления. Данная способность базируется на обменных операциях полиномиальной системы классов вычетов. В настоящее время проявляется повышенный интерес к возможности варьирования корректирующей способностью модулярного кода за счет изменения точности и производительности вычислений в пределах одного цифрового устройства. В первую очередь это объясняется тем, что учет указанного свойства полиномиальной системы классов вычетов является мощным средством повышения надежности, т.е. при отказе r каналов их можно просто удалить из процессора, не оказывая влияния на точность выполнения задания. Но, с другой стороны, данные r избыточных каналов предопределяют корректирующие способности вычислительной системы, другими словами – гарантию защиты от недостоверного результата.
Таким образом, изменяя количество информационных и избыточных оснований в заданной структуре специализированных процессоров полиномиальной системы классов вычетов, можно варьировать его основными показателями – точностью, информационной надежностью вычислительной системы. Если некоторая упорядоченная полиномиальная система классов вычетов расширяется путем добавления оснований, каждое из которых больше основания исходной полиномиальной системы классов вычетов, то минимальное кодовое расстояние автоматически увеличивается [1].
Того же эффекта можно добиться, уменьшая число информационных оснований, т.е. переходя к вычислениям с меньшей точностью. На одном и том же специализированных процессоров можно одни и те же вычисления выполнять с высокой точностью, но с меньшей информационной надежностью или с меньшей точностью, но с более высокими значениями надежности и скорости.
Таким образом, очевидно, что полиномиальная система классов вычетов обладает свойством, позволяющим ей гибко использовать резервы точности и надежности при наличии ограничений на увеличение веса, габаритов и стоимости цифрового устройства. Внедрение математической модели полиномиальной системы классов вычетов, позволяющей представлять числа в модулярном коде, является одним из наиболее перспективных путей повышения отказоустойчивости и быстродействия вычислительных средств цифровой обработки сигналов. В этом случае преимущества модулярной арифметики реализуются наиболее полно, как в направлении обеспечения высокой отказоустойчивости, так и в направлении повышения производительности функционирования специализированных процессоров цифровой обработки сигналов.
Рецензенты:
Пашинцев В.П., д.т.н., профессор кафедры информационной безопасности автоматизированных систем, Институт информационных технологий и телекоммуникаций, ФГАОУ ВПО «Северо-Кавказский федеральный университет», г. Ставрополь;
Линец Г.И., д.т.н., профессор, заведующий кафедрой инфокоммуникаций, Институт информационных технологий и телекоммуникаций, ФГАОУ ВПО «Северо-Кавказский федеральный университет», г. Ставрополь.