Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Аэродинамическим качеством крыла называется отношение коэффициента подъемной силы C_y к коэффициенту аэродинамического сопротивления C_x:

.

Считается, что наилучшими аэродинамическими свойствами обладает крыло с максимальным значением аэродинамического качества K [1]. Для воздушного винта сила тяги F_у и мощность P, затрачиваемая на вращение с частотой f, определяются следующим образом [2]:

,                                             (1)

,                                                 (2)

где ρ - плотность воздуха, D - диаметр воздушного винта, A(a) и B(a) - безразмерные коэффициенты тяги и мощности, соответственно, зависящие от геометрических параметров винта и угла установки α. Это позволяет для воздушного винта ввести величину

,                                              (3)

аналогичную аэродинамическому качеству крыла. При этом величина A(a)ρ=F_y/f²D⁴ представляет собой приведенную силу тяги, а величина B(α)ρ=P/f³D⁵ - приведенную мощность, поэтому отношение (3) - ничто иное, как отношение приведенной силы тяги к приведенной мощности, затрачиваемой на вращение воздушного винта. По аналогии с аэродинамическим качеством крыла можно предположить, что наилучшими аэродинамическими свойствами обладает винт с максимальным значением K_w.

С другой стороны, исключая из выражений (1) и (2) частоту вращения f, можно получить выражение

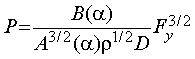.                                            (4)

Получается, что для обеспечения минимальных потерь энергии при заданной силе тяги и при заданном диаметре винта D минимумом должен обладать коэффициент

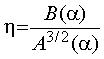,                                                        (5)

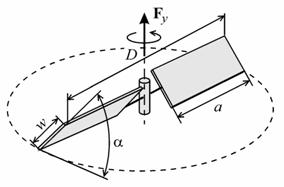
а не B(α)/A(α). Поскольку та и другая величины зависят от угла установки a, то сравнивать следует условия минимумов функции η(α) и зависимости B(α)/A(α) от a. Речь, разумеется, идет о сравнении и обработке экспериментальных зависимостей. Результат должен быть воспроизводимым, поддаваться экспериментальной проверке и теоретическому анализу, поэтому в качестве примера имеет смысл изучить аэродинамические свойства воздушного винта с плоскими лопастями (рис. 1). Существенной силой тяги, как оказалось, обладает воздушный винт с параметрами w/D=0.13 и a/D=0.4.

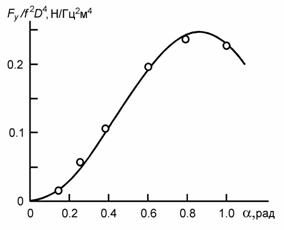
Рис. 2 демонстрирует зависимость приведенной силы тяги от угла установки a. В этой зависимости нет ничего неожиданного; приближенно зависимость силы тяги от угла установки и геометрических параметров крыла может быть описана функцией

   (6).                         

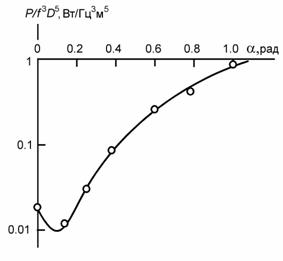
Неожиданным оказалось появление минимума мощности, затрачиваемой на вращение воздушного винта при малых углах установки (рис. 3). Чем это вызвано у воздушного винта с плоскими лопастями, до конца не понятно, хотя и имеет очень важное значение. Для винта с лопастями, обладающими профилем с ненулевой толщиной, это является привычным следствием лобового сопротивления крыла или воздушного винта [3].

Зависимость мощности P от угла установки, частоты вращения и диаметра ротора приближенно может быть описана функцией

.          (7)

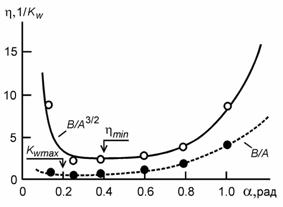
Теперь есть все, чтобы установить соответствие между двумя подходами к выбору параметров воздушного винта. Результаты такого анализа, проведенные с использованием полученных экспериментальных данных и приближенных зависимостей (6) и (7), представлены на рис. 4 и демонстрируют существенные различия между оптимальными значениями угла установки. Минимум коэффициента η=B(α)/A^3/2(α) соответствует значению a_3/2 ≈ 0.4, тогда как максимальное значение аэродинамического качества воздушного винта K_w наблюдается при a₁ ≈ 0.2. При этом потери энергии (4) при a=a₁ почти в полтора раза больше, чем при a=a_3/2. Минимум потерь энергии, показанный на рис. 3, здесь не причем: он наблюдается при a≈0.1.

Важно отметить, что максимальное отношение коэффициенты K_w оказалось равным 1.67, разумеется, не совпадающим со значением тангенса угла, при котором "качество воздушного винта" имеет максимальное отношение. Так оно должно и быть, поскольку коэффициенты A(α) и B(α) определяют величины, имеющие совершенно разный смысл, - силу и мощность. Это - еще одна причина попытки определять оптимальный угол установки лопасти воздушного винта, исходя из так называемой поляры (рис. 5), считать бессмысленными. С другой стороны, потери энергии пропорциональны силе аэродинамического сопротивления [4], поэтому интерпретация отношения A(α)/B(α) как аэродинамического качества воздушного винта понятна, но ничем не обоснована. Есть одно единственное оправдание для построения поляры воздушного винта. Это - необходимость продемонстрировать сравнение результатов расчетов, использующих приведенные выше аппроксимации (6) и (7), с экспериментальными данными. К сожалению, в известной мере основной результат может быть перенесен и на выбор оптимальных параметров крыла. Для крыла, обладающего профилем это должно быть особо заметно. Основой для таких критических замечаний явились экспериментальные исследования, опирающиеся на прецизионные измерения потерь энергии, методика которых основана на изучении динамики твердого тела, вращающегося в среде [5]. В оптимальном режиме воздушный винт с плоскими лопастями является достаточно экономичным. Например, для того, чтобы создать силу тяги 100Н, требуется мощность двигателя менее 3 л.с. при диаметре крыла всего лишь 1 м.

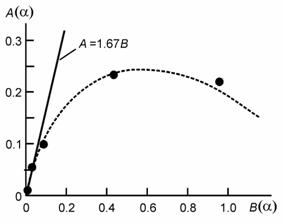
Рис. 5. Поляра воздушного винта. Точки - экспериментальные результаты, кривая - расчет по формулам (6) и (7), прямая линия соответствует максимальному значению аэродинамического качества K_w.

СПИСОК ЛИТЕРАТУРЫ:

1. Краснов Н.Ф. Аэродинамика. Ч. 1. Основы теории. Аэродинамика профиля и крыла. М.: Высшая школа, 1976. 384 c.
2. Прицкер Д.М., Сахаров Г.И. Аэродинамика. М.: Машиностроение, 1968. 310 с.
3. Anderson D., Eberhardt S. Understanding Flight. New York: McGraw-Hill, 2001. 240 p.
4. Герасимов С.А. Потери энергии вращающимся в среде твердым телом. // Фундаментальные исследования. 2008. № 3. С. 97-99.
5. Герасимов С.А. Об измерении потерь энергии вращающимся крылом. // Техника и технология. 2008. № 3. С. 10-12.