Задачи прогнозирования нефтегазоносности всегда были актуальными, а в наше время, в сложных экономических условиях, качество их решения имеет особое значение. Они решаются на основе изучения геологического строения крупных регионов, динамических особенностей развития, построения моделей тектонического и геологического строения региона. Таким образом, важно наличие адекватных реальной среде геолого-геофизических моделей осадочных бассейнов и их фрагментов, построенных на основании комплексного анализа всей имеющейся геолого-геофизической информации.
Одним из главных факторов, определяющим эффективность использования геофизических методов для решения задач построения моделей геологических сред, является заложенная в поле полезная информация об исследуемом объекте и возможность извлечения этой информации. Рассмотрим технологии реконструкции структурно-плотностных моделей по гравиметрическим данным [8]. Коснёмся некоторых, наиболее популярных и представляющих интерес в связи с поставленной проблемой.
Различные технологии интерпретации гравиметрических данных в своей основе содержат решение соответствующих обратных задач. Под решением обратной задачи [6] понимают нахождение распределения источников x (плотность σ(v) или конфигурация границ f(s)) по заданным наблюдаемому полю U и оператору прямой задачи A(x):
Ax = U. (*)
Одна из технологий основана на призматическом подходе (Е.Г. Булах, С.В. Шалаев, В.И. Старостенко, П.И. Балк, В.И. Гольдшмидт, В.Н. Страхов и др.). Уступы, призмы, пирамиды, цилиндры, многоугольники – наиболее распространённые геометрические объекты, набором которых с подобранными геометрическими параметрами и плотностями моделируется реальный геометрический объект. Такой способ решения обратных задач – метод подбора, где в качестве модельного класса выбираются конструкции призматического типа. В рамках этих методов для решения обратных задач (*) рассматриваются:
1. Модельный класс k – множество возможных элементарных тел m, которыми аппроксимируется геологическая среда. Для каждого элементарного тела существует способ расчёта компоненты гравитационного поля u = A(x) и наблюдённая компонента un.
2. Критерий подбора наблюдённого и рассчитанного полей представлен минимизируемым функционалом J(un, A(m)), характеризующим степень согласия изучаемых компонент гравитационного поля.
3. Алгоритм решения обратной задачи представляет собой способ осуществления минимизации функционала J(un, A(m)), в результате чего определяется искомая плотностная модель m′.
В зависимости от задания гравитационного поля и его точности, наличия регионального фона, влияния пород, залегающих вне области поиска решения и т.п., принимается различный вид функционала J(un, A(m)).
В рамках методов подбора можно выделить также технологии, состоящие в нахождении некоторых формальных источников наблюдаемого гравитационного поля с последующим их эквивалентным перераспределением [12]. При описании сложнопостроенных сред число параметров значительно возрастает, и при решении обратной задачи методами подбора возникают проблемы устойчивости и единственности. Решение вопросов о корректности обратных задач занимает в теории интерпретации геофизических данных центральное место. Так, трудами А.Н. Тихонова, М.М. Лаврентьева, В.Н. Страхова и их последователей развита теория некорректных задач. В основе этой теории лежит идея привлечения в постановку обратной задачи дополнительной информации об искомом решении. Непосредственно поиск решения обратной задачи осуществляется с помощью регуляризирующих алгоритмов [1, 11]. Проблема неединственности обратной задачи сопровождается её неустойчивостью: малые изменения во входных данных порождают различные результаты решения. Снижение этого эффекта позволило осуществить методы регуляризующих процедур. При решении обратных задач для сложнопостроенных сред возникает «эффект скрытой эквивалентности» [1, 2, 3, 5]. Для реально существующего распределения плотности σ(v), характеризующего изучаемую среду, найдётся элемент m*, такой что для достаточно малого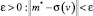 
. На исходном классе может найтись также некоторый бессмысленный с геологической точки зрения элемент σ′(v), такой что A(σ(v)) = A(σ′(v)), который может быть аппроксимирован некоторым элементом m′ из класса K лучше, чем m*, аппроксимирует σ(v) [2]. Возникает вопрос о том, какое решение из области эквивалентности получается при использовании метода подбора.
Особый интерес представляют технологии, развивающие методы решения обратных задач гравиметрии в рамках так называемого критериального подхода, разработанного А.И. Кобруновым [5]. Особенность данного подхода состоит в том, что на основе критерия качества решения, содержащего в свёрнутом виде априорную информацию о параметрах среды, из множества решений, удовлетворяющих наблюдённому гравитационному полю формируются классы единственности, а полученные на них решения обратной задачи удовлетворяют условиям единственности и устойчивости [5]. Вопросы, связанные с такой постановкой обратной задачи, широко отражены в трудах В.Н. Страхова [15], А.И. Кобрунова [1], А.С. Маргулиса, М.В. Новоселицкого [7] и др. Подобная постановка известна в работах G. Backus и F. Gilbert [14], разработавших линейную теорию решения обратных задач при использовании ограниченного набора данных. Подробная характеристика этих методов дана в [13]. Основы данной технологии заложены в системе GCIS, разработанной А.И. Кобруновым, А.П. Петровским и др. [4], но все эти технологии – двухмерные. В этой ситуации необходимо обеспечить увязку технологий профильного и объёмного моделирования.
Технологии, основанные на спектральном анализе поля, представлены в работах Л.Т. Бережной, М.А. Телепина, О.И. Журавлевой и др. Для нахождения плотности используется полиномиальная аппроксимация, а описание конфигурации плотностной границы производится отрезком ряда Фурье. Восстановление геометрии модели по полю проводилось при помощи сферических функций. В случае нескольких контактных поверхностей возникает проблема выделения из суммарного поля гравитационных эффектов от каждой поверхности и изучения трансформации полей. Необходимо оценивать качество решения.
Одной из объёмных технологий построения пространственных моделей является технология корреляционного прогнозирования структур. Они были развиты в работах В.И. Шрайбмана, М.С. Жданова, О.В. Витвицкого, Г.И. Каратаева, Ф.М. Гольцмана, Т.Б. Калининой, А.А. Никитина и др. В общей схеме для расчётов выбираются эталонный и исследуемый участки, близкие по геологическому строению. По данным различных исследований на эталонном участке устанавливается корреляционная связь между глубиной плотностной границы и какой-либо компонентой гравитационного поля. Составленное уравнение регрессии применяется к исследуемому участку. Результаты решений во многом зависят от степени соответствия эталонной и исследуемой площадей, от полученной тесноты связи на эталонной площади. Проблемным вопросом является выделение аномального гравитационного поля, наилучшим образом связанного с конкретной плотностной границей. На сегодняшний день корреляционно-статистическими методами интерпретировано большое количество данных. Например, на территории Тимано-Печорской провинции и Баренцевоморского бассейна была проведена обработка данных С.П. Аплоновым [10] и др.
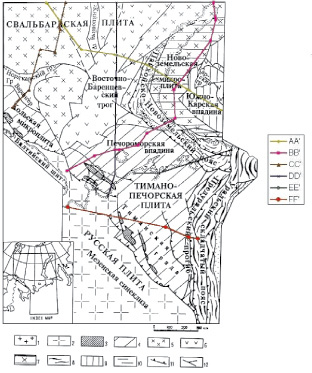
Рис. 1. Тектоническая карта района исследований (Выкопировка из тектонической схемы севера Европейской части России и прилегающих акваторий [10]): 1 – фундамент Балтийского щита; 2 – протерозойский фундамент, перекрытый чехлом Русской плиты; 3 – складчатые рифейско-вендские отложения; 4 – эпибайкальские плиты; 5 – эпигренвильская плита; 6 – троги с субокеанической корой; 7 – эпигренвильская плита с элементами киммерийской складчатости; 8 – герцинские складчатые структуры; 9 – эпигерцинская плита; 10 – раннекиммерийские складчатые структуры; 11 – надвиги; 12 – сбросы, сдвиги
Результаты такого анализа являются приближенными. Объясняется это тем, что физическая информация в уравнениях, описывающих модель, просто не используется. Поэтому итоговая модель зависит от того, в какой последовательности и какие профили были взяты за эталон, какие из них были взяты для проверки. При замене одних другими может получиться другая структура, и доказательством тому является сопоставление результатов построения Тимано-Печорской провинции и Баренцевоморского бассейна (рис. 1) при различных подходах к представлению априорной информации.
На рис. 2 и 3 представлены результаты построения рельефа фундамента одной и той же территории различных авторов [9, 10]. Расхождения достигают 8000 м, что приводит к выводу о необходимости пересмотра выполненных построений, проверки их на соответствие гравитационному полю и корректировки. Необходимо вернуться к изучению строения осадочных бассейнов, даже там, где были проведены исследования и составлены структурные карты.
Таким образом, существующие сегодня технологии анализа гравиметрических данных не позволяют качественно решать задачу изучения сложнопостроенных образований типа осадочных бассейнов в условиях фрагментарности данных. Это связано либо с недостаточностью возможности комплексирования, либо недостатками, скрытыми в технологии гравитационного анализа при решении обратных задач. Проведённый анализ эффективности применения гравиразведки при решении задач поиска нефти и газа показал, что при интерпретации геофизических данных не в полной мере используется информация, содержащаяся в гравитационном поле.
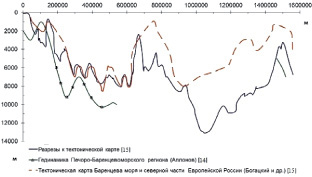
Рис. 2. Сопоставление рельефа поверхности фундамента по профилю BB′
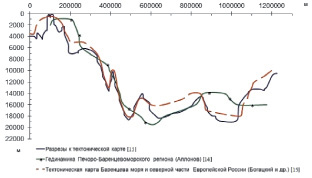
Рис. 3. Сопоставление рельефа поверхности фундамента по профилю DD′
В этой связи необходимо развитие специализированной методики, основанной на решении обратных задач в условиях фрагментарности данных. Активное использование априорной информации в технологиях решения обеспечит управление процессом получения единственного элемента из класса эквивалентности, а также технологичность процедур и содержательность результатов.
Рецензенты:
Бурмистрова О.Н., д.т.н., заведующая кафедрой технологии и машин лесозаготовок, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта;
Андронов И.Н., д.т.н., заведующий кафедрой сопротивления материалов и деталей машин, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта.