Заметим, что при составлении расчетной модели приведенной крутильной системы не учитывались переменные силы внутреннего трения в материале коленчатого вала (упругий гистерезис), так как они невелики по сравнению с силами жидкостного трения в подшипниках и цилиндрах двигателя.
Приведенная n-массовая крутильная система коленчатого вала ДВС (рис. 1) в общем виде описывается системой дифференциальных уравнений, которые запишем в матричном виде:
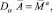 (1)
(1)
где Dts – матрица, учитывающая свойства приведенной крутильной системы [Dts = f(Ii, w, Сi,i + 1, Ci + 1,I, ξi)]; 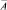 – вектор-столбец амплитуд крутильных колебаний масс;
– вектор-столбец амплитуд крутильных колебаний масс; 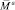 – вектор-столбец амплитуд гармонических составляющих моментов, действующих в крутильной системе.
– вектор-столбец амплитуд гармонических составляющих моментов, действующих в крутильной системе.
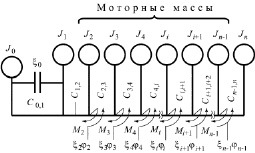
Рис. 1. Приведенная n-массовая эквивалентная крутильная система коленчатого вала ДВС
Для определения амплитуд вынужденных колебаний примем, что массы i (i = 0,1, 2, …, n) при вынужденных колебаниях совершают гармонические колебания одной и той же частоты [4, 5, 6]:
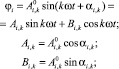 (2)
(2)
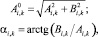 (3)
(3)
где 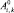 – k-я гармоническая амплитуда массы i, рад; ai,k – фазовый угол амплитуды k-й гармоники массы i, град; w – угловая частота возмущающего момента, рад·с–1; k – порядок гармоники возмущающего момента.
– k-я гармоническая амплитуда массы i, рад; ai,k – фазовый угол амплитуды k-й гармоники массы i, град; w – угловая частота возмущающего момента, рад·с–1; k – порядок гармоники возмущающего момента.
Возмущающий момент на каждую моторную массу представим в виде
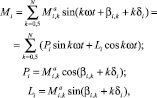 (4)
(4)
где N – число гармоник (0,5; 1,0; 1,5; …N, для двухтактных двигателей – 1, 2,0, …, N); 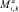 – амплитуда k-й гармоники возмущающего момента Mi, действующего на массу i от газовых и инерционных сил, Н.м; βi,k – ее фазовый угол, град; δi – угол поворота коленчатого вала между вспышками в первом и i-ом цилиндрах двигателя, град.
– амплитуда k-й гармоники возмущающего момента Mi, действующего на массу i от газовых и инерционных сил, Н.м; βi,k – ее фазовый угол, град; δi – угол поворота коленчатого вала между вспышками в первом и i-ом цилиндрах двигателя, град.
Таким образом матрица-столбец 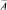 содержит по два компонента амплитуд крутильных колебаний масс Ii, а матрица-столбец
содержит по два компонента амплитуд крутильных колебаний масс Ii, а матрица-столбец 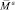 содержит нулевые компоненты – по два для масс I0, I1 и In , так как на них не действуют никакие вынуждающие моменты (для экономии места для векторов
содержит нулевые компоненты – по два для масс I0, I1 и In , так как на них не действуют никакие вынуждающие моменты (для экономии места для векторов 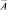 и
и 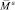 используем строчечную запись):
используем строчечную запись):
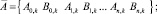
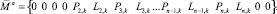 (5)
(5)
Матрица Dts – квадратная, имеющая порядок 2n, где n – число масс в приведенной крутильной системе. По своей структуре она является ленточной, поскольку только на главной диагонали, а также на двух верхних и двух нижних кодиагоналях располагаются отличные от нуля элементы. Для подробного анализа разобьем матрицу Dts на блоки Dii, которые сами являются квадратными матрицами второго порядка:
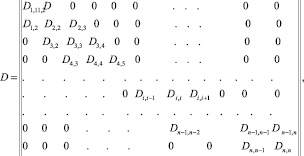 (6)
(6)
где 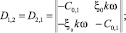
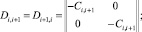 (7)
(7)
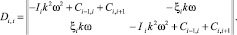 (8)
(8)
Блоки D1,2 = D2,1 описывают связь между массами I0 и I1 – учитывается коэффициент жесткости C0,1 на этом участке приведенной системы, а также сопротивление крутильным колебаниям, вызванное демпфером – ξ0kω. Для демпфера жидкостного трения C0,1 = 0, т.е. на главной диагонали располагаются нулевые компоненты. Если между какими-то массами приведенной системы отсутствует демпфирование, то компоненты, стоящие на побочной диагонали, равны нулю (ξi = 0). Для моторных масс, имеющих собственное демпфирование (переменные силы жидкостного трения в подшипниках и цилиндрах), сопротивление учитывается компонентом ξikω Матрица несимметрична, поскольку при дифференцировании угловой координаты φi (2) по времени t функция cos kωt при Bi,k – нечетная.
Блоки несимметричных матриц Dii, расположенные на главной диагонали, учитывают свойства i-й массы – ее момент инерции, демпфирование собственно самой массы, а также коэффициенты жесткости участков приведенной системы перед массой и после нее. Несимметричность блоков матрицы Dts вызвана как раз тем, что функция cos kωt при Bi,k – нечетная.
Умножив матричное уравнение (1) слева на матрицу D–1, обратную матрице D, получим
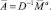 (9)
(9)
Решение (9) легко реализуется на ЭВМ. Расчет компонентов матрицы D можно провести по формулам (8) и (9).
Матрица-столбец амплитуд гармонических составляющих вынуждающих моментов, действующих на массы i, может быть определен на основе гармонического анализа кривой крутящего момента двигателя. Для вычисления амплитуд необходимо подставить поочередно в уравнение (10) значение амплитуд вынуждающих моментов для всех гармоник, начиная с 0,5 (и с таким же шагом) для четырехтактного или с 1,0 – для двухтактного. Амплитуды и фазовые углы колебаний и фазовые углы для каждой массы i и гармоники определяются по формуле (3).
Для определения суммарной амплитуды угловых колебаний Ai i-ой массы от угла поворота коленчатого вала двигателя воспользуемся зависимостью
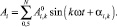 (10)
(10)
Численное решение системы (1) приведенной крутильной системы коленчатого вала ДВС с помощью ЭВМ позволяет выбрать такой демпфер крутильных колебаний, при котором амплитуды колебаний носка будут минимальными [7, 8]. На рис. 2 приведена структурная схема оптимизации коэффициента демпфирования и момента инерции маховика демпфера внутреннего трения. Предварительно нужно оптимизировать коэффициент жесткости резинового слоя C0,1. Из условий компоновки на носке коленчатого вала демпфера внутреннего трения выбираются ориентировочно его габаритные размеры. Величина динамического коэффициента жесткости демпфера C0,1 можно определить по формулам [8, 9]:
для резинового слоя цилиндрической формы
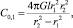 (11)
(11)
где G – модуль упругости второго рода резинового слоя; r1 и r2 – внутренний и внешний радиусы резинового кольца; l – ширина демпфера;
для резинового слоя демпфера Г-образной формы
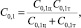 (12)
(12)
где C0,1ц определяется по (11); C0,1ц = GIp/Lт – коэффициенты жесткости слоя в торцевой поверхности соответственно; Ip – полярный момент инерции его; lт – размер резинового слоя в торцевой поверхности.
Вместе с тем, как показывают расчеты, значение коэффициента жесткости резинового слоя C0,1 можно определить следующим образом. После расчетов по формулам (11)–(12) определяются пределы изменения C0,1. Необходимо иметь в виду, что по (11) и (12) определяют статический коэффициент жесткости Cjст, а для определения динамического коэффициента Cφд необходимо умножить полученное значение Cφст на 2…2,5. Кроме того, при работе двигателя демпфер нагревается до температуры t = 50…60 °С и динамическая жесткость резинового слоя изменяется [10].
Для определения зависимости Cφд от температуры демпферы устанавливались на безмоторной установке и нагревались потоком теплого воздуха или охлаждались до температуры минус 20 °C. После обработки результатов экспериментальных исследований получена следующая эмпирическая зависимость, позволяющая определить действительное значение динамического коэффициента жесткости Cφд (при известном статическом C0) резинового слоя при изменении температуры t:
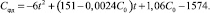 (14)
(14)
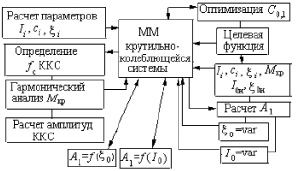
Рис. 2. Структурная схема оптимизации коэффициента демпфирования и момента инерции маховика демпфера внутреннего трения
Покажем на конкретном примере выбор резинового слоя для демпфера для коленчатого вала дизеля с воздушным охлаждением 6ЧН 10,5/12.
Пример расчета резинового демпфера
Дизель 6ЧН 10,5/12 с показателями: номинальная мощность Ne = 76 кВт; среднее эффективное давление pe = 0,68 МПа; номинальная частота вращения коленчатого вала n = 2200 мин–1; порядок работы цилиндров 1-5-3-6-2-4.
Параметры девятимассовой приведенной крутильной системы коленчатого вала дизеля 6ЧН 10,5/12 приведены в табл. 1, а результаты гармонического анализа кривой крутящего момента одного цилиндра в табл. 2.
Расчетом было установлено, что круговая частота свободных крутильных колебаний по первой форме (табл. 2) составляет ωс1 = 1364 с–1 (частота f1 = 217 Гц), а те же параметры по второй форме колебаний – ωс2 = 2935 с–1 (f2 = 467 Гц). Демпфирование каждой моторной массы составляет по расчету [3] ξi = 2,18 Н×м×с.
После расчета резонансных крутильных колебаний выяснилось, что на частотах вращения 1448, 1738, 2172 и 2890 мин–1 (для гармоник 9-й, 7,5-й, 6-й и 4-й) амплитуды носка (масса 1), а также касательные напряжения в узловой точке превышают допустимые (рис. 3 и 4 – кривые 1). Так, в пределах рабочих частот амплитуда крутильных колебаний носка коленчатого вала достигает A1 = 13·10–3 рад, а касательные напряжения tmax = 60 МПа.
По нашим исследованиям [1, 4, 5] на резонансных режимах уровень касательных напряжений не должен превышать 15…25 МПа. В связи с этим было принято решение об установке резинового демпфера крутильных колебаний.
Выбрав из условий компоновки габаритные размеры демпфера, по формуле (13) определим ориентировочные значения динамического коэффициента жесткости: C0,1 = 10000…40000 Н·м. Начальное значение момента инерции маховика демпфера выбрали I0 = 0,014 кг·м2.
Таблица 1
Параметры приведенной крутильной системы дизеля коленчатого вала 6ЧН 10,5/12
|
Моменты инерции масс приведенной крутильной системы, кг·м2·10–2 |
|||||||||||||||
|
I0 |
I1 |
I2 |
I3 |
I4 |
I5 |
I6 |
I7 |
I8 |
|||||||
|
1,40 |
0,75 |
5,64 |
3,89 |
5,64 |
5,64 |
3,89 |
5,64 |
69,2 |
|||||||
|
Коэффициенты жесткости, Н·м·104 |
|||||||||||||||
|
C0,1 |
C1,2 |
C2,3 |
C3,4 |
C4,5 |
C5,6 |
C6,7 |
C7,8 |
||||||||
|
2,295 |
7,64 |
116 |
116 |
116 |
116 |
116 |
145 |
||||||||
Таблица 2
Гармонический анализ кривой крутящего момента одного цилиндра дизеля 6ЧН 10,5/12
|
Гармоника k |
Mi,kа, Н·м |
bi,k, град |
Гармоника k |
Mi,kа, Н·м |
bi,k, град |
|
0,5 |
139,0 |
249°33′ |
5,0 |
58,1 |
326°33′ |
|
1,0 |
168,94 |
28°15′ |
5,5 |
49,6 |
149°38′ |
|
1,5 |
143,0 |
196°20′ |
6,0 |
41,8 |
323°11′ |
|
2,0 |
97,65 |
169°41′ |
6,5 |
35,1 |
138°38′ |
|
2,5 |
118,9 |
180°28′ |
7,0 |
29,3 |
314°27′ |
|
3,0 |
10,4 |
329°41′ |
7,5 |
24,5 |
130°19′ |
|
3,5 |
91,4 |
177°08′ |
8,0 |
20,7 |
307°04′ |
|
4,0 |
69,6 |
346°55′ |
8,5 |
17,7 |
122°32′ |
|
4,5 |
67,4 |
162°38′ |
9,0 |
14,9 |
298°18′ |
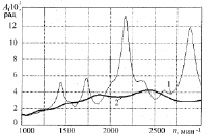
Рис. 3. Изменение амплитуд угловых колебаний первой массы приведенной системы коленчатого вала дизеля 6ЧН 10,5/12 от частоты вращения: 1 – без демпфера; 2 – с резиновым демпфером
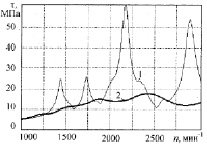
Рис. 4. Изменение касательных напряжений в узловом сечении коленчатого вала дизеля 6ЧН 10,5/12 от частоты вращения: 1 – без демпфера; 2 – с резиновым демпфером
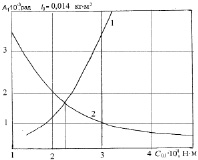
Рис. 5. Зависимость резонансных амплитуд A1 колебаний первой массы от коэффициента жесткости резинового слоя с моментом инерции маховика I0 = 0,014 кг·м2: 1 – изменение A1 по первой форме; 2 – то же – по второй форме
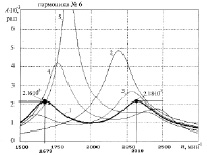
Рис. 6. Амплитуда крутильных колебаний массы 2 при изменении жесткости резинового слоя C0,1, Н·м: 1 – 22950; 2 – 10000; 3 – 20000; 4 – 30000; 5 – 40000

Рис. 7. Изменение амплитуды крутильных колебаний носка коленчатого вала дизеля 6Н 10,5/12 (Д-160) при n = 2200 мин–1 по углу поворота коленчатого вала j: – расчетные; - экспериментальные данные
Для приведенной крутильной системы коленчатого вала дизеля 6ЧН 10,5/12 найдем максимальную амплитуду крутильных колебаний первой массы A1 при изменении C0,1 от 10000 до 40000 Н·м по первой и второй формам колебаний. Результаты этих расчетов приведены на рис. 5. На основании их примем значение коэффициента жесткости резинового слоя C0,1 = 22950 Н·м @ 23000 Н·м, (на пересечении кривых 1 и 2) поскольку при увеличении C0,1 амплитуда колебаний по первой форме (кривая 1) резко возрастает. Частота свободных крутильных колебаний демпфера равна ωд = 1281 с–1. На рис. 6 приведена амплитудно-частотная характеристика для массы 2 многомассовой крутильно-колеблющейся системы коленчатого вала дизеля 6ЧН 10,5/12 (Д-160) при изменении коэффициента жесткости резинового слоя демпфера (I0 = 0,014 кг·м2).
Значение логарифмического коэффициента затухания по результатам наших исследований [8, 10] d = 0,87. Отсюда легко определяется начальное значение коэффициента демпфирования в резиновом слое ξ0 = 5,45 Н·м·с.
Результаты расчетов амплитуды крутильных колебаний, а также касательных напряжений в узловой точке приведенной системы с выбранным резиновым демпфером приведены на рис. 3.23 и 3.24 (кривые 2), из которых следует, что для первой массы амплитуда A1 уменьшилась в 3,17 раза, а касательные напряжения в узловой точке – в 4 раза.
На рис. 7 приведены расчетные и экспериментальные кривые амплитуд крутильных колебаний носка A1 коленчатого вала 6ЧН 10,5/12 (Д-160) по углу его поворота с резиновым демпфером (I0 = 0,014 кг·м2; C0,1 = 2,3·104 Н·м; ξ0 = 5,5 Н·м·с) [3] на номинальной частоте вращения n = 2200 мин–1.
Рецензенты:
Кобзев А.А., д.т.н., профессор, заведующий кафедрой, ФГБОУ «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых», г. Владимир;
Кульчицкий А.Р., д.т.н., профессор, главный специалист ООО «Завод инновационных продуктов» КТЗ, г. Владимир.



