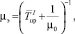Для обеспечения качественного функционирования сети связи создается система технического обслуживания и ремонта, представляющая собой, как правило, смешанную многоуровневую систему, в состав которой входят центры технического обслуживания и ремонта, осуществляющие управление техническим состоянием входящих в зону обслуживания данного центра средств. Эффективность выполнения системой связи возложенных на неё задач во многом определяется качеством функционирования системы технического обслуживания и ремонта.
Для обеспечения качественного функционирования сетей связи создается система технического обслуживания и ремонта (СТОР). При проектировании и построении СТОР необходимо учитывать ряд особенностей сети связи как объекта эксплуатации, таких как:
– территориальная рассредоточенность элементов сети;
– многофункциональность системы, реализация на основе первичной сети нескольких вторичных;
– взаимосвязь различных средств системы;
– разнотипность средств, различия их по эксплуатационным свойствам и надежности.
СТОР современных сетей связи строится, как правило, с использованием элементов централизованного и децентрализованного принципа построения и представляет собой смешанную многоуровневую систему [1, 7]. При таком построении создаются центры технического обслуживания и ремонта (ЦТОР), на которые и возлагаются задачи по управлению техническим состоянием средств сети связи, входящих в данную зону обслуживания. Обслуживание средств при этом осуществляется либо выездными бригадами ЦТОР, либо доставкой нуждающихся в обслуживании средств в ЦТОР.
Очевидно, что качество функционирования сети связи в значительной мере будет определяться способом построения и функционирования СТОР, тем, насколько эффективно выполняет СТОР возложенные на неё задачи. Поэтому уровень требований к свойствам создаваемой СТОР может быть обоснованно назначен лишь на основе анализа функционирования комплекса: объект эксплуатации – СТОР.
Цель исследования – разработка показателя, использующегося для оценки готовности восстанавливаемых систем с сетевой структурой. Таким показателем является коэффициент готовности информационного направления 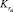 (вероятность связности двух произвольных абонентов сети S и t) [2, 6, 8], под которым будем понимать вероятность того, что в произвольный момент времени между заданной парой полюсов S и t окажется хотя бы один работоспособный простой путь. Отметим, что причиной нарушения связи между абонентами может быть не полное отсутствие связи между ними, а снижение пропускного потока по сети между данными вершинами ниже некоторого заданного уровня. Однако данные аспекты в части.
(вероятность связности двух произвольных абонентов сети S и t) [2, 6, 8], под которым будем понимать вероятность того, что в произвольный момент времени между заданной парой полюсов S и t окажется хотя бы один работоспособный простой путь. Отметим, что причиной нарушения связи между абонентами может быть не полное отсутствие связи между ними, а снижение пропускного потока по сети между данными вершинами ниже некоторого заданного уровня. Однако данные аспекты в части.
Исходные предположения и допущения метода исследования
При оценке качества функционирования сети связи и СТОР интерес могут представлять также и ряд других показателей, таких как среднее число средств, находящихся на обслуживании, среднее время пребывания средств на обслуживании, среднее время наработки на отказ информационного направления, среднее время восстановления работоспособности информационного направления и другие.
Модель для расчета перечисленных показателей описывается следующим образом.
Сеть произвольной структуры, представленная графом, содержит K узлов связи, в составе которых используются R типов средств, различающихся по целевым функциям и параметрам надежности. Число средств типа η (η = 1, R) на k-м узле равно 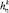 , общее число средств равно H. Задана также матрица расстояний между элементами сети
, общее число средств равно H. Задана также матрица расстояний между элементами сети
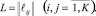
Сеть обслуживают N центров технического обслуживания и ремонта. Обратим внимание, что число ЦТОР меньше числа узлов. В состав каждого ЦТОР входит ρn бригад 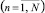 , где общее число бригад меньше суммарного количества обслуживаемых средств. Каждый ЦТОР силами входящих в его состав бригад обслуживает одно из подмножеств элементов сети. При этом в общем случае эти подмножества могут быть пересекающимися, т.е. определенные элементы сети связи могут быть обслужены двумя и более ЦТОР.
, где общее число бригад меньше суммарного количества обслуживаемых средств. Каждый ЦТОР силами входящих в его состав бригад обслуживает одно из подмножеств элементов сети. При этом в общем случае эти подмножества могут быть пересекающимися, т.е. определенные элементы сети связи могут быть обслужены двумя и более ЦТОР.
Наличие в ЦТОР ρn бригад учитывается зависимостью интенсивности обслуживания в данном центре от количества заявок на обслуживание ln:
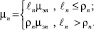 (1)
(1)
Величина μэ представляет собой интенсивность обслуживания заявок одной бригадой и определяется в зависимости от принятого в данной системе алгоритма работы ЦТОР. Если обслуживание элементов сети связи осуществляется выездными бригадами ЦТОР, причём после удовлетворения заявки бригада возвращается обратно в ЦТОР, то μэ можно определить как это сделано в [7]:
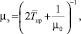 (2)
(2)
где 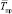 – среднее время, затрачиваемое бригадой на движение между ЦТОР и элементом сети;
– среднее время, затрачиваемое бригадой на движение между ЦТОР и элементом сети; 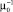 – среднее время, затрачиваемое бригадой на выполнение операций по обслуживанию.
– среднее время, затрачиваемое бригадой на выполнение операций по обслуживанию.
Если бригады действуют автономно, т.е. после обслуживания одного элемента сети могут не возвращаться в ЦТОР, а перемещаться к следующему элементу, требующему обслуживания (что обычно имеет место в условиях большой загрузки), то μэ можно определить как
где 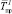 – среднее по всем маршрутам между элементами сети и СТОР время, затрачиваемое бригадой на движение. В том случае, когда средства, требующие обслуживания, доставляются в ЦТОР, и бригады не затрачивают времени на передвижения, μэ = μ0.
– среднее по всем маршрутам между элементами сети и СТОР время, затрачиваемое бригадой на движение. В том случае, когда средства, требующие обслуживания, доставляются в ЦТОР, и бригады не затрачивают времени на передвижения, μэ = μ0.
Пусть имеется также ремонтный орган, осуществляющий восстановление средств и в случаях, когда это невозможно сделать силами ЦТОР (например, капитальный ремонт). После восстановления каждое средство возвращается туда же, откуда оно поступило.
Таким образом, в рассматриваемой системе имеет место ограниченное неоднородное восстановление. Причем события, состоящие в работоспособности элементов, обслуживаемых одним ЦТОР, являются зависимыми.
Постановка задачи исследований
Для определения показателей качества функционирования системы связи и СТОР целесообразно использовать аппарат локально сбалансированных сетей массового обслуживания [3, 4].
Система связи совместно с центрами технического обслуживания и ремонта и ремонтным органом формализованно могут быть представлены в виде открытой неоднородной сети массового обслуживания, состоящей из M = N + P систем массового обслуживания (СМО) и внешнего источника. При этом CMOm (m = 1, N) имитирует процессы функционирования центров технического обслуживания и ремонта по удовлетворению заявок на ТО и ремонт, а остальные СМО описывают процессы появления заявок на обслуживание и ремонт. Внешний источник моделирует процесс функционирования ремонтного органа.
Движение заявок по сети массового обслуживания и распределение зон обслуживания описываются маршрутной матрицей 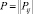 , в которой Pio и Poj соответственно вероятность поступления заявок из i-й системы в ремонтный орган и вероятность возвращения из ремонтного органа в j-й центр; Pij – вероятность поступления заявок из CMOi в CMOj, причём
, в которой Pio и Poj соответственно вероятность поступления заявок из i-й системы в ремонтный орган и вероятность возвращения из ремонтного органа в j-й центр; Pij – вероятность поступления заявок из CMOi в CMOj, причём 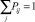 (i = 1, M), т.е. каждый элемент обслуживается хотя бы в одном из центров.
(i = 1, M), т.е. каждый элемент обслуживается хотя бы в одном из центров.
Разработка математических моделей выбора оптимального варианта
Пусть состояние такой сети массового обслуживания определяется матрицей
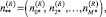 (4)
(4)
где 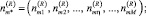
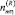 – количество заявок класса η, находящихся в CMOm.
– количество заявок класса η, находящихся в CMOm.
В [4] для стационарного режима приведено выражение для определения вероятности 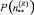 того, что открытая сеть массового обслуживания находится в состоянии
того, что открытая сеть массового обслуживания находится в состоянии 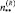 :
:
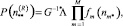 (5)
(5)
где G – нормализующая константа
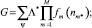 (6)
(6)
здесь Λ* – интенсивность входящего (выходящего) потока заявок на обслуживание; ψ – множество всех возможных состояний сети массового обслуживания; fm(nm*) – функция, вид которой определяется в зависимости от характеристик центра обслуживания, дисциплины обслуживания и характеристик потока заявок.
При этом подсистемы элементов сети связи без резервирования, а также подсистемы элементов с нагруженным резервированием могут быть описаны [3, 4] системами массового обслуживания типа I S (тип СМО, где число обслуживающих приборов не меньше суммарного количества заявок), допускающими произвольное распределение наработки на отказ, но имеющими рациональное преобразование Лапласа. Подсистемы элементов с ненагруженным или комбинированным резервом описываются СМО типа FCFS (тип СМО, в которых требования обслуживаются в порядке их поступления) с числом обслуживающих приборов, равным числу активно работающих элементов. Распределение наработки на отказ при этом допускается экспоненциальное.
Функция fm(nm*) в этих случаях имеет следующий вид [4]:
 (7)
(7)
где emη определяется из системы линейных уравнений
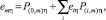
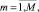
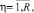 (8)
(8)
а P(i,m)η – вероятность перехода заявки класса η из CMOi в CMOm.
Обслуживание заявок на ТО и ремонт в CMOm 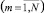 может осуществляться в соответствии с функциями FCFS, LCFS или RAND. Для СМО с функцией FCFS допускается при этом экспоненциальное распределение времени обслуживания, для двух других функций – произвольные с рациональными преобразованиями Лапласа и средними
может осуществляться в соответствии с функциями FCFS, LCFS или RAND. Для СМО с функцией FCFS допускается при этом экспоненциальное распределение времени обслуживания, для двух других функций – произвольные с рациональными преобразованиями Лапласа и средними 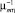 . При этом fm(nm*) определяется [4]:
. При этом fm(nm*) определяется [4]:
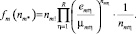 (9)
(9)
С использованием стационарных вероятностей состояний сети массового обслуживания 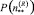 могут быть определены требуемые показатели качества функционирования системы технического обслуживания и ремонта сети связи.
могут быть определены требуемые показатели качества функционирования системы технического обслуживания и ремонта сети связи.
Коэффициент готовности информационного направления 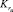 , под которым понимается вероятность того, что в произвольный момент времени между заданной парой полюсов S t окажется хотя бы один работоспособный простой путь, может быть определен как сумма вероятностей нахождения сети массового обслуживания во множестве ψst всех тех состояний, при которых имеется хотя бы один такой путь:
, под которым понимается вероятность того, что в произвольный момент времени между заданной парой полюсов S t окажется хотя бы один работоспособный простой путь, может быть определен как сумма вероятностей нахождения сети массового обслуживания во множестве ψst всех тех состояний, при которых имеется хотя бы один такой путь:
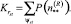 (10)
(10)
Среднее число средств, находящихся на обслуживании и ожидающих обслуживания –j-м ЦТОР, есть среднее число заявок, находящихся в очереди и на обслуживании в СМО, имитирующей функционирование данного ЦТОР и определяется следующим образом:
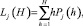 (11)
(11)
где Pj(h) – вероятность нахождения сети массового обслуживания в состояниях, когда в CMOj и в очереди находится h заявок на обслуживание. Заметим при этом, что Lj(H) не зависит от функций обслуживания заявок при следующих условиях [5]:
– пока в системе есть неудовлетворенные требования, обслуживающие механизмы не прекращают функционировать;
– обслуживание любого требования доводится до конца;
– дисциплина очереди не основана на приоритете динамического типа.
Среднее время простоя 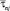 элемента сети связи, входящего в зону обслуживания j-го ЦТОР, складывается из времени, затрачиваемого собственно на восстановление работоспособности, и времени ожидания обслуживания по причине отсутствия свободных бригад. Для CMOj, имитирующей работу j-го ЦТОР, среднее время пребывания в очереди и на обслуживании может быть определено с использованием формулы Литтла [4, 5]:
элемента сети связи, входящего в зону обслуживания j-го ЦТОР, складывается из времени, затрачиваемого собственно на восстановление работоспособности, и времени ожидания обслуживания по причине отсутствия свободных бригад. Для CMOj, имитирующей работу j-го ЦТОР, среднее время пребывания в очереди и на обслуживании может быть определено с использованием формулы Литтла [4, 5]:
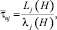 (12)
(12)
где λj(H) – средняя интенсивность входящего в CMOj суммарного потока заявок на обслуживание.
Знание среднего времени наработки на отказ элемента сети связи и среднего времени простоя позволяет определить величину коэффициента готовности данного элемента 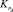 .
.
Введем в рассмотрение понятие структурной функции, имеющей существенное значение в задачах определения показателей надежности структурно-сложных систем, в частности сетей связи [6, 8].
Результаты исследования и их обсуждение
Если в качестве модели функционирования информационного направления выбрана модель системы, которая может находиться в двух состояниях:
в состоянии работоспособности, когда существует хотя бы один работоспособный простой путь между заданной парой полюсов S и t не существует;
система состоит из элементов, которые в свою очередь могут находиться только в двух состояниях – работоспособном и неработоспособном, то структурная функция S связывает состояние системы Y с состоянием элементов Xi, из которых состоит данная система:
Y = S(X1, X2, …, Xn),
где Xi – булева переменная, описывающая состояние i-го элемента сети связи;

Y – булева переменная, описывающая состояние информационного направления S–t:

Если структурная функция S построена, то показатель надежности системы определяется как вероятность равенства структурной функции единице, а коэффициент готовности информационного направления 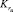 связан с коэффициентами готовности элементов
связан с коэффициентами готовности элементов 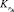 соотношением
соотношением
 (13)
(13)
где 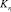 и
и  – коэффициенты готовности S-го и t-го элементов (входного и выходного полюсов) и произведён переход от функций алгебры логики к вероятностным функциям.
– коэффициенты готовности S-го и t-го элементов (входного и выходного полюсов) и произведён переход от функций алгебры логики к вероятностным функциям.
Для расчета среднего времени наработки на отказ информационного направления 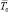 можно воспользоваться соотношением [6]:
можно воспользоваться соотношением [6]:
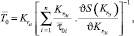 (14)
(14)
где 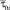 – среднее время наработки на отказ i-го элемента сети.
– среднее время наработки на отказ i-го элемента сети.
Для некоторых частных случаев выражение (14) можно упростить. Для этого воспользуемся леммой, доказанной в [2]:
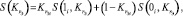 15)
15)
где 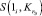 и
и 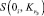 – структурные функции системы, в которой i-й элемент находится в заведомо работоспособном и в заведомо отказовом состояниях соответственно. Применив разложение (15) структурной функции, записанной для информационного направления S-t относительно полюса S, получим
– структурные функции системы, в которой i-й элемент находится в заведомо работоспособном и в заведомо отказовом состояниях соответственно. Применив разложение (15) структурной функции, записанной для информационного направления S-t относительно полюса S, получим
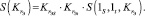 (16)
(16)
Если между парой полюсов S и t существует несколько простых путей, а элементы, составляющие эти пути, высоконадежны, причем среди них нет, кроме полюсов, элементов, отказ которых однозначно приводит к отказу всего информационного направления (что, как правило, имеет место в реальных сетях связи), то 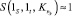 и
и 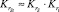 , т.e. готовность информационного направления S – t определяется в основном готовностью полюсов S и t. В этом случае выражение (14) преобразуется к виду
, т.e. готовность информационного направления S – t определяется в основном готовностью полюсов S и t. В этом случае выражение (14) преобразуется к виду
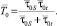 (17)
(17)
Среднее время восстановления работоспособности информационного направления рассчитывается по известными 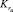 и
и 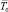 :
:
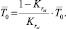 (18)
(18)
Предполагаемая модель позволяет производить расчет ряда показателей качества функционирования системы технического обслуживания и ремонта сетей связи и может быть использована при решении задач оптимизации структуры и алгоритмов функционирования СТОР, при определении степени централизации СТОР, а также при расчёте показателей надежности структурно-сложных восстанавливаемых систем.
Выводы
Предполагаемая модель позволяет производить расчет ряда показателей качества функционирования системы технического обслуживания и ремонта сетей связи и может быть использована при решении задач оптимизации структуры и алгоритмов функционирования СТОР, при определении степени централизации СТОР, а также при расчёте показателей надежности структурно-сложных восстанавливаемых систем.
Рецензенты:
Козлов В.В., д.т.н., профессор кафедры, ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург;
Смагин В.А., д.т.н., профессор кафедры, ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург.