Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

В настоящее время интеллектуальные системы, основанные на знаниях, получили широкое распространение в различных прикладных областях для решения таких задач, как прогнозирование, распознавание образов, диагностика, управление и другие [2]. Основным компонентом интеллектуальных систем является база знаний, включающая набор правил принятия решений, выраженных в форме четких или нечетких продукций. Использование нечетко-продукционных правил позволяет решать практические задачи в условиях нечеткости, неопределенности и неполноты исходных данных.

Для формирования правил базы знаний в последнее время все чаще применяют методы автоматического формирования нечетких правил, основанные на методах и алгоритмах интеллектуального анализа данных. Использование такого подхода значительно упрощает и ускоряет процесс разработки интеллектуальной системы. Однако, несмотря на его достоинства, автоматически сформированные базы знаний, как правило, обладают избыточностью, что не позволяет использовать их с максимальной эффективностью при решении практических задач. Для повышения эффективности использования интеллектуальных систем требуется оценка избыточности и редукция их баз знаний [1]. Проведенный анализ показал, что существующие подходы к редукции нечетких правил не лишены недостатков, в частности возможности снижения точности принимаемых решений на основе редуцированных баз знаний. Это актуализирует необходимость разработки и апробации новых эффективных методов и алгоритмов редукции нечетких правил в базах знаний интеллектуальных систем. Таким образом, для повышения эффективности использования интеллектуальных систем в работе решается задача разработки кластерно-генетического метода редукции нечетких правил, основанного на алгоритме их кластеризации и генетическом алгоритме минимизации числа кластеров.

Кластерно-генетический метод редукции нечетких правил

В основу разработанного метода редукции нечетких правил положены принципы таксономии знаний (кластеризации нечетких правил) [3], а также эволюционного моделирования (генетической оптимизации) [4]. Обобщенная схема кластерно-генетического метода представлена на рис. 1.

Разработанный метод редукции нечетких правил состоит из 2-х этапов:

1) кластеризация (таксономия) нечетких правил в исходной базе знаний с получением промежуточной базы знаний, состоящей из правил, соответствующих центрам кластеров;

2) редукция нечетких правил промежуточной базы знаний на основе генетического алгоритма, позволяющего минимизировать число правил и сформировать искомую базу знаний.

Рассмотрим каждый из этапов более подробно. Пусть имеется исходная база знаний R = {R₁, R₂, …, R_m}, где R_i (i = 1…m) – нечетко-продукционные правила Такаги – Сугено вида

ЕСЛ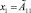И 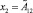И И … 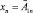ТО y = B1,

ЕСЛ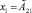И 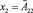И И … 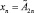ТО y = B2,

…

ЕСЛ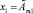И 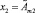И И … 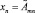ТО y = Bk,

где x₁, ..., x_n – входные лингвистические переменные; 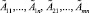– их нечеткие значения; y – четкая выходная переменная; B₁, ..., B_k – классы решений.

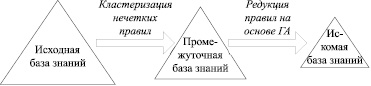
Рис. 1. Схема кластерно-генетического метода редукции нечетких правил

Представим антецеденты нечетких правил в виде вектора их нечетких ограничений. Тогда система правил примет следующий вид:

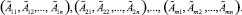(1)

Перейдем от нечетких множеств 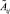(i = 1...m, j = 1...n) к их четким аналогам xij, используя процедуру дефаззификации по методу центра тяжести:

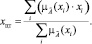
После дефаззификации выражение (1) примет вид

(x₁₁, x₁₂, …, x_1n), (x₂₁, x₂₂, …, x_2n), …, (x_m1, x_m2, …, x_mn).

Таким образом, исходная база знаний представляется точками в n-мерном Евклидовом пространстве, количество координат которых соответствует количеству входных параметров нечетких правил. Следовательно, задача таксономии нечетких правил сводится к задаче кластеризации полученных точек данных.

В общем случае значения входных параметров нечетких правил измерены в разных шкалах, поэтому перед кластеризацией необходимо произвести нормировку дефаззифицированных значений антецедентов, используя метрику вида

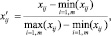
где 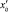– исходное значение параметра; 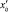– нормированное значение.

Результатом данной процедуры является множество точек в нормированном n-мерном пространстве:

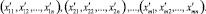
Таксономию знаний необходимо производить независимо для каждого класса решений, поэтому перед ее выполнением необходимо разделить множество точек данных на подмножества по классам решений и в каждом из них кластеризацию производить отдельно.

На рис. 2 представлена блок-схема разработанного алгоритма кластеризации с получением промежуточной базы знаний.

В качестве алгоритма кластеризации точек данных выбран расширенный алгоритм k-средних, благодаря его масштабируемости (возможности работы с большими массивами данных) и способности работать с разнотипными параметрами. При выборе лучшего кластерного решения необходимо руководствоваться критерием ошибки обобщения, получаемой интеллектуальной системой при ее работе на тестовой выборке данных:

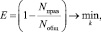
где N_прав – число правильно классифицированных примеров; N_общ – общее число примеров.

В полученном кластерном решении центры кластеров могут как совпадать с имеющимися правилами в базе знаний (физические центры кластера), так и не совпадать с ними (логические центры кластеров). В последнем случае возникает задача идентификации значений параметров функций принадлежности нового нечеткого правила, соответствующего данной точке. Для ее решения разработан численный метод (метод средних координат). Рассмотрим пример идентификации значений параметров треугольной функции принадлежности.

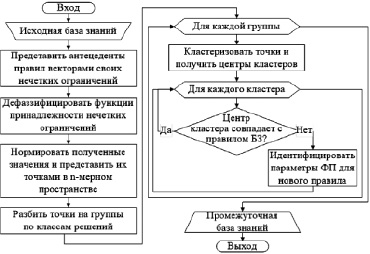
Рис. 2. Блок-схема алгоритма кластеризации

Треугольная функция принадлежности задается тройкой чисел {l, c, r}, при этом функция принадлежности определяется по следующей формуле:

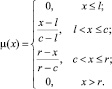
Необходимо получить значения параметров функций принадлежности, соответствующих каждой координате из N точек кластера (l_ij, c_ij, r_ij) и для каждой j-й координаты логического центра кластера вычислить значения параметров функции принадлежности по следующим формулам:

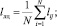
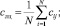
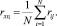
Результатом кластеризации нечетких правил в исходной базе знаний является промежуточная база знаний, состоящая из правил, соответствующих центрам кластеров. Для минимизации правил (удаления незначимых центров кластеров) используется редукция нечетких правил на основе генетического алгоритма, позволяющего минимизировать число сформированных кластеров.

Пусть имеется промежуточная база знаний R = {R₁, R₂, …, R_m}, содержащая множество нечетких правил R_j, j = 1...m, где m – объем базы знаний. Закодируем базу знаний в виде хромосомы

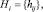
где

Создание начальной популяции объемом m выполняется следующим образом: в популяцию включается родительская хромосома и набор потомков, полученных в результате случайной мутации ее генов с вероятностью 0,02.

Задача редукции нечетких правил сводится к поиску хромосомы, позволяющей достичь максимума оценки классифицирующей способности базы знаний (не меньше исходной точности классификации) при минимальном числе активных правил. Таким образом, используемая в генетическом алгоритме фитнесс-функция имеет вид

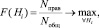
где N_прав – число правильно распознанных примеров в выборке данных; N_общ – ее объем.

Рассмотрим реализацию генетических операторов.

На этапе селекции производится отбор 2-х родительских хромосом из начального хромосомного набора, используя метод колеса рулетки. В данном методе вероятность выбора хромосомы определяется следующим образом:

.

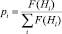Оператор скрещивания позволяет получать 2-х потомков от родительских хромосом на основе одно- и двухточечного кроссинговера.

Мутация осуществляется путем инверсии с вероятностью 0,02 одного из единичных генов дочерних хромосом.

После определения приспособленности дочерних хромосом выполняется оператор редукции, в результате которого происходит удаление 2-х худших хромосом из текущего хромосомного набора и формируется новая популяция.

Данный алгоритм выполняется до тех пор, пока в результате вычислений не будут появляться хромосомы с лучшей функцией приспособленности в течение определенного числа поколений. После окончания его работы отбирается одна хромосома с лучшими значениями фитнесс-функции, которая и будет определять искомую базу знаний интеллектуальной системы.

Исходя из условий и ограничений применимости разработанных методов и алгоритмов, предъявляются следующие требования к редуцируемой базе знаний:

1) большая размерность;

2) тип базы знаний: нечетко-продукционная с кусочно-линейными функциями принадлежности нечетких антецедентов;

3) задача, решаемая на правилах базы знаний: задача классификации;

4) известен алгоритм логического вывода на правилах базы знаний;

5) база знаний сформирована автоматически на основе методов и алгоритмов машинного обучения (например, нейронных сетей);

Сравнение исходных и редуцированных баз знаний

6) доступны все экспериментальные данные, на основе анализа которых сформирована база знаний.

Для оценки эффективности математического обеспечения редукции нечетких правил в базах знаний интеллектуальных систем разработан программный комплекс в среде Matlab.

Проведение исследований на базе программного комплекса

Для проведения исследований на базе разработанного программного комплекса использован набор данных для решения задачи выявления нестандартных транзакций с банковскими картами из общедоступного источника UCI Machine Learning Repository [5]. Исходная выборка данных включала 690 записей по 14 входным параметрам и одному выходному с двумя классами решений (стандартные и нестандартные транзакции).

Формирование исходных баз знаний (с использованием треугольных и трапециевидных функций принадлежности) выполнено на основе нечеткой нейронной сети ANFIS. Результаты проведенных исследований показали, что редуцированные базы знаний показывают лучшие свойства классифицирующей способности и скорости логического вывода по сравнению с исходными базами знаний (таблица).

Таким образом, редукция баз знаний интеллектуальных систем на базе разработанного математического обеспечения приводит к устранению избыточности баз знаний, повышению классифицирующей способности и интерпретируемости базы знаний, а также повышению скорости принятия решений.

Заключение

Описанные в работе математическое обеспечение и программный комплекс позволяют редуцировать нечеткие правила в базах знаний интеллектуальных систем. Проверка работы программного комплекса на известных наборах данных показала высокую эффективность разработанного математического обеспечения и практическую пригодность программного комплекса к решению поставленных задач.

Рецензенты:

Песошин В.А., д.т.н., профессор кафедры компьютерных систем, Казанский национальный исследовательский технический университет им. А.Н. Туполева – КАИ, г. Казань;

Кирпичников А.П., д.ф.-м.н., профессор, заведующий кафедрой интеллектуальных систем и управления информационными ресурсами, Казанский национальный исследовательский технологический университет, г. Казань.