Впервые Эрмит ввел положительные формы вида
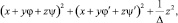(1)
где х, y, z – тройки возможных целых рациональных чисел; φ и ψ – кубические иррациональности; ∆ – переменный параметр. Изменяя последовательно значения параметра ∆, можно получать системы (х, y, z), которые определяют минимумы квадратичных форм. Так как такая конструкция приводит к анализу выражений (форм), имеющих квадраты компонент элементов кубических полей, то естественно назвать ее методом квадратичных форм (МКФ).
Алгоритм (принцип) Эрмита представляет собой одну из разновидностей МКФ как совокупность действий, позволяющих находить последовательные минимумы квадратичных форм с переменным параметром.
Е.И. Золотарев использовал алгоритм Эрмита для разыскания основной единицы чисто кубического поля. Его идея основана на изучении последовательных минимумов некоторых положительных тернарных квадратичных форм с непрерывным параметром и последующем сведении этой задачи к аналогичной проблеме применительно к бинарным формам.
Предварительно Е.И. Золотарев [4] рассматривает задачу разыскания представлений последовательных минимумов для бинарной квадратичной формы
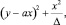(2)
которая содержит непрерывный параметр ∆, являющийся инвариантом формы и принимающий различные значения от 1 до ∞. Эти представления (х′, y′) для ∆, ∆′ ≤ ∆ ≤ ∆″, (х″, y″) для ∆, ∆″ ≤ ∆ ≤ ∆‴ связаны соотношениями:
1) х, y – возрастают;
2) х′y″ – х″y′ = ±1; х″y‴ – х‴y′′ = ±1;
3) 
4) φ′ > φ″ > φ‴ > …
1) 
…
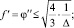
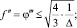2) первый минимум: ∆ = 1, х′ = 0, y′ = 1;
второй минимум: х″ = 1, y″ = m0,
где 
,
для третьего минимума
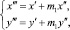
здесь m1 таково, что |y‴ – ах‴| < y″ – ах″ и т.д.
Далее Золотарев переходит к тернарной квадратичной форме
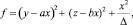(3)
и представления минимумов определяются тройками
(х′, y′, z′) для ∆, ∆′ ≤ ∆ ≤ ∆″;
(х″, y″, z″) для ∆, ∆″ ≤ ∆ ≤ ∆‴.
Анализ уравнений (2) и (3) позволяет Золотареву перейти к решению главной задачи – разысканию основной единицы чистого кубического поля 
.
Пусть 
– единица 
, тогда
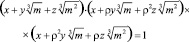(4),
где ρ3 = 1.
Полагаем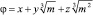 
, а произведение двух последних скобок дает союзную форму F(х, y, z), причем
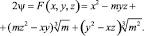
В соответствии с этим составим квадратичную форму
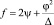(5)
с инвариантом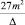 
.
Как известно, при любом ∆ найдется тройка (х, y, z) такая, что 
откуда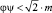 
.
Увеличиваем ∆ и для каждого ∆ найдем тройки (х′, y′, z′) и (х″, y″, z″), дающие min f, получим
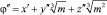
и соответственно 2φ′ и 2φ″.
Все произведения φψ – целые числа, и в их ряду φ′ψ′, φ″ψ″… существует хоть одно число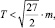 
повторяющееся бесконечное число раз. Тем самым определятся две системы (a, b, g) и (α′, β′, γ′) такие, что
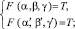
a ≡ α′; β ≡ β′; γ ≡ γ′ (mod T).
Далее полагаем
α′2 – mβ′γ′ = А′; m′γ2 – α′β′ = В′;
β′2 – α′γ′ = С′,
α2 – mβΥ = А; mγ2 – αβ = В; β2 – αΥ = С.
Пусть теперь
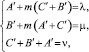
а подстановка λ = uT, μ = υT, ν = wT приводит к уравнению
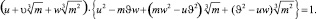
Если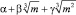 
– основная единица 
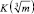, то компоненты αn, βn, λn остальных всех единиц, как известно, выразятся по формулам
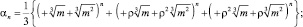
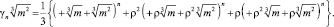
Компоненты основной единицы составят тройку, находящуюся в ряду minima квадратичной формы (5) для различных значений параметра ∆. Действительно, если (х, y, z) – основная единица, то х = α2 – mβg; y = mγ2 – αβ; z = β2 – αγ и (х, y, z) дает min формы 
, ε > 1.
В этих условиях ψ обращается в ε, φ – в ε–1.
Последовательность min правой части (5) приведет к условиям
φ0 = 1; ψ0 = 1; φ1 > φ0; ψ1 < ψ0; φ2 > φ1;
ψ2 < ψ1 и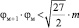 
.
Введем периодически повторяющиеся величины
Lм = φм∙ψм+1; Kм = φм+1∙ψм; Hм = φм∙ψм.
Имеет место очевидное соотношение
Lм∙Kм = Нм + Нм+1,
и для компонент справедливы оценки
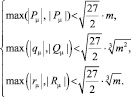
Из уравнения
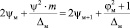
определяем
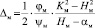, (6)
и для всех комбинаций (Kм, Lм) выбирают ту, для которой (6) минимально. Тогда если мы дойдем до Нs = 1, то Кs > 1, Ls < 1 и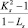 
даст минимум, далее получаем: Hs + 1 = H1; Hs + 2 = H2, …
Из этих рассуждений очевидно, что требование нахождения всех последовательных минимумов по принципу Эрмита влечет громоздкие и долгие расчеты. В настоящее время подобные и более сложные расчеты не представляют больших сложностей, так как они реализуются с использованием специальных компьютерных технологий.
Приведем пример нахождения основной единицы вручную.
Пример.
m = 11,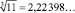 
х0 = 1; y0 = 0; z0 = 0; φ0 = 1; ψ0 = 1.
Это даст
z0 = 1; х0 = 0; y0 = 0; М0 = 0; N0 = –1; Р0 = 0,
β = 1; a = 0; γ = 0; β1 = 0; γ1 = 1; α1 = 1.
Далее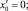 
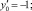
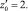
Полагая
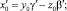
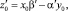
находим:
α′ = α1 + 2a = 0; β′ = β1 + 2β = 2;
γ′ = γ1 + 2γ = 1.
Отсюда
х1 = α′ + m1α = m1; y1 = β′ + m1β = 2;
z1 = γ′ + m1γ = 1,
т.е. m1 = 4 или 5.
При m1 = 4
Если же m1 = 5, то
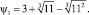
Но корень уравнения f1 = f0 для указанных значений m1 будет меньше во 2 случае, и, таким образом, х1 = 5; y1 = 2; z1 = 1.
Унимодулярные преобразования формы F0 и союзной формы F по формулам
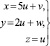и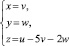 
приведут к форме
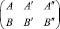
и союзной ей
,
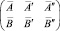где A = A′; B″ = 0,719; B′ ≈ –2,11;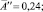 
.
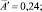
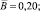
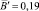Итак, тройка (x, y, z) = (5; 2; 1) определяет минимум, смежный с f0.
Продолжаем вычисления. Имеем x1 = 0; y1 = 1; z1 = –2, откуда M1 = –1; N1 = 0; P1 = 5.
Дальнейшее вычисление минимумов даёт
x2 = 20; y2 = 9; z2 = 4; M2 = 0; N2 = 4; P2 = –9;
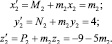
Легко находим: m2 = –2 и компоненты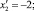 
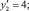
определяют искомую основную единицу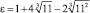 
чисто кубического поля 
Оставляя основную идею сведения, разработанную Золотаревым, Успенский [5] модифицировал всю конструкцию, распространив ее на кубические поля отрицательного дискриминанта. Такое видоизменение позволило упростить практические расчеты.
Суть его в следующем. Предварительно в кубическом поле Dλ < 0 показывается, что всегда можно выбрать нормальный базис вида {1, α, β}, где α, β – целое рациональное число, причем на базисном элементе α достигается минимум некоторого выражения, а именно: выполняется неравенство
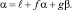
Составим аналогично (5) положительно определенные формы
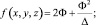
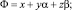
где Δ – непрерывный положительный параметр, и союзную форму
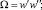
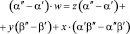
дискриминанта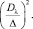 
В основе последующего вывода лежит утверждение: для всякого конкретного значения Δ существуют две триады (x, y, z) и (X, Y, Z), не содержащие общих множителей, и такие, что
1) X∙x + Y∙y + Z∙z = 0;
2) выполняются неравенства
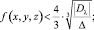
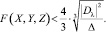
Очевидно, если Δ будет расти, то одна из триад должна быть заменена другой по специальным формулам. Это произойдет либо относительно первой триады (x, y, z) при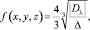 
либо применительно ко 2-й триаде (X, Y, Z) при условии
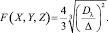
Указанное будет иметь место при
1) 
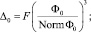
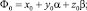
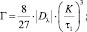
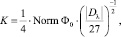
где τ1 – наименьший положительный корень уравнения
τ3 – τ + K = 0; (7)
2) 
,
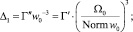
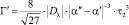где τ2 – наибольший положительный корень уравнения (7).
Начальному значению Δ соответствуют триады
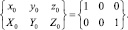
Пусть Δ растет. Определив Δ0 и Δ1, сравним их между собой.
Если Δ0 < Δ1, то триада (x0, y0, z0) заменяется новой триадой. При Δ0 > Δ1 аналогичное преобразование выполняется для 2-й триады. Тем самым определяется бесконечная цепочка пар триад
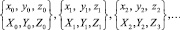
и две серии соответствующих значений Φ и w:
Ф0 = 1, Ф1, Ф2, Ф3, …, w0 = 1, w1, w2, w3, …
Пусть ε > 1 – прямая основная единица, ε–1 – обратная ей единица. Продолжив цепочку триад достаточно далеко, можно получить искомую единицу, а ею будет первая единица в одной из этих последовательностей.
Пример. Чисто кубическое поле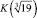 
[2] имеет целый базис
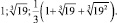
В качестве нормального базиса берем элементы
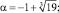
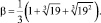
Для него имеем
f = –3; g = 3; k = 2; ℓ = –1;
α ≈ 1,668; β = 3,596
и
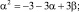
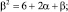
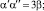
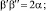
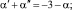
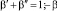
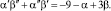
Начинаем расчеты с Φ0 = 1, w0 = 1.
Тогда k = 0,04; Γ = Δ = 318,4 и k = 0,12; Γ1 = Δ1 = 13,74.
1 шаг. Пусть M = –1, α = 0, N = 1 откуда
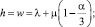
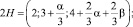
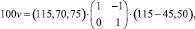
где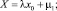 
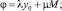
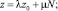
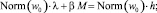
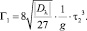
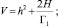
Н = Norm(w0)∙h′h″L.
В нашем случае
λ = 1; μ = –1; 
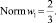
Пусть теперь k = 0,08. Далее находим: Γ1 = 14,83 и Δ1 = 84,35.
Переходим ко второму шагу.
2 шаг. N = 1, L = 0, M = 0 и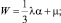 
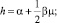
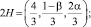
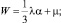
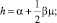
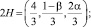
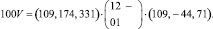
Отсюда λ = 2; μ = –1 и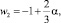 
Norm w2 = 1; k = 0,12; Γ1 = 13,74; Δ1 = 970,5.
3 шаг. Из условия Φ = λ – (α + 2β)∙μ имеем λ = 5; μ = –1; Φ1 = 5 + α + 2β; Norm Φ1 = 1.
Таким образом, найдена алгебраическая единица, и так как она не является степенью другой единицы, то она должна быть основной единицей.
Итак,
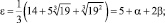
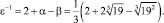
Рассуждения, опирающиеся на чисто кубические поля и основную единицу в них, используются в доказательствах неразрешимости уравнения Ферма в кубическом случае [3], а сами основные единицы используются при вычислении числа классов идеалов и решений многих частных типов и классов диофантовых уравнений [1].
Рецензенты:
Алтухов В.И., д.ф.-м.н., профессор, ведущий научный сотрудник отдела стратегического и инновационного развития, Институт сервиса, туризма и дизайна (филиал), ФГАОУ ВПО СКФУ, г. Пятигорск;
Казуб В.Т., д.т.н., профессор, заведующий кафедрой физики и математики, Пятигорский медико-фармацевтический институт, филиал ГБОУ ВПО ВолгГМУ Минздрава РФ, г. Пятигорск.