Вопросам моделирования электрических сетей энергосистемы уделяется пристальное внимание, начиная с момента появления первых автоматизированных систем проектирования (САПР) и автоматизированных систем диспетчерского управления (АСДУ) на основе ЭВМ. Модели дают возможность проверять реальность и оптимальность проектных разработок по отдельным энергетическим объектам и энергосистеме в целом, а также проверять надежность функционирования работающей энергосистемы путем решения конкретных технологических задач. Это позволяет производить сравнительный анализ разных стратегий проектирования и оперативного управления для принятия решений на основании состояния параметров режима электрической сети [1].
Из множества моделей электрической сети энергосистемы в общем случае можно выделить два основных типа моделей, используемых при решении задач проектирования и оперативного управления режимами её работы.
Первый тип - это общепринятая графическая модель электрической схемы энергосистемы, описывающая в требуемом объёме и степени детализации оборудования электрической сети и отдельные объекты. Такой моделью, например, является электрическая схема сети энергосистемы или её фрагменты, представленные упрощенными или полными схемами первичных соединений электростанций и подстанций с элементами оборудования, на бумажных носителях, мозаичном диспетчерском щите или в электронном виде в ПЭВМ.
Второй тип это специализированные модели расчетных схем, описывающие максимально-упрощеную схему электрической сети энергосистемы без элементов оборудования на уровне требований применяемых математических методов и конкретных технологических задач, например, узловая расчетная схема электрической сети энергосистемы для решения задачи оценки установившегося режима или токов короткого замыкания.
С момента начала внедрения ЭВМ в электроэнергетику и до настоящего времени при решении технологических задач, в частности расчетов нормальных и аварийных режимов энергосистемы, применяются упрощенные расчетные модели второго типа, так называемые узловые модели, описываемые примитивами "узлы" и "ветви". За этими моделями при решении инженерных задач, как в проектировании, так и в эксплуатации энергосистем, сохраняется приоритет и по настоящее время. Такое положение объясняется требованиями формализации и алгоритмизации используемых математических методов, существующей технологией расчетов, возможностями эксплуатируемой в проектировании и производстве вычислительной техники.
Современный уровень технических и программных средств позволяет реализовать задачу автоматического преобразования модели первого типа в расчетную модель второго типа для выполнения расчета, сохраняя при этом исходные параметры, состояние оборудования и коммутационных аппаратов рассматриваемого режима работы энергосистемы. Такая универсальная модель обеспечивает быстрое решение всего состава технологических задач, анализ полученных результатов и своевременную выработку последующей стратегии проектирования или оперативного управления.
В качестве исследуемого объекта для оценивания состояния в задаче определения режимной надежности рассматривается часть энергосистемы (рис. 1), включающая в себя транзитные линии 110 кВ.
Первый тип модели представлен на рисунке 1. Расчетная модель второго типа для решения задачи расчета установившегося режима основывается на решении УУР в форме баланса мощностей методом Ньютона или минимизации уравнений с применением весовых коэффициентов.
Все параметры режима связаны в каждый момент времени системой уравнений установившегося режима:
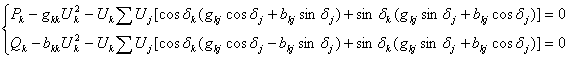 (1)
(1)
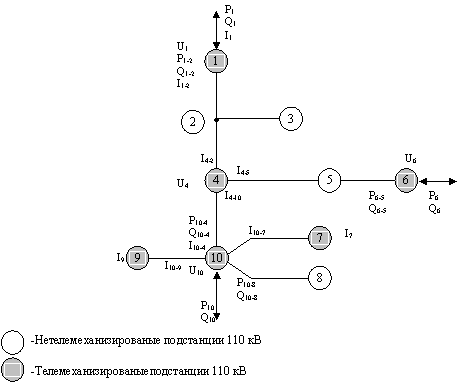
Рис. 1. Структурная схема 110кВ. части энергосистемы с исходными данными телеметрии
Из вектора измерений для приведенной схемы можно выделить базисный состав (мощности нагрузок, генерирующих узлов, напряжение базисного узла) и избыточный вектор (I4-2, I4-5, I4-10, P10-4, Q10-4, напряжения узлов).
При этом контрольные уравнения для избыточных измерений будут выглядеть как:
![]() ;
;
![]() (2)
(2)
![]()
![]()
График нагрузки каждого потребителя, значения которой являются случайными величинами, можно считать случайным процессом. Применив регрессионный анализ измеренных значений в соответствии со временем, можно получить аналитическую функцию для нагрузки потребителей или для мощностей и токов проходящих в транзитных линиях энергосистемы.
Модель линейной регрессии имеет вид: y = mx + b или y = m1x1 + m2x2 + ... + b в случае для многомерной линейной регрессии, где зависимое значение y является функцией независимого значения x. Значения m - это коэффициенты, соответствующие каждой независимой переменной x, а b - постоянная.
Модель линейной регрессии нагрузки потребителя относительно временного интервала будет выглядеть так:
![]() .
.
В случае нормального закона распределения статистической информации:
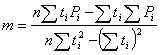 ,
, 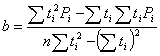
Для примера на рисунке 2 представлен график аппроксимирующей функции и активной мощности узла 1 с выборкой по рабочему дню недели (среда) в течение двух месяцев.
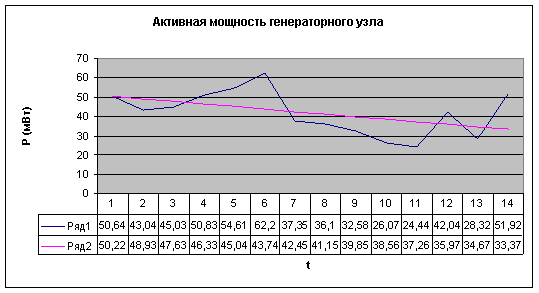
Рис. 2. Активная мощность генераторного узла
Для оценки ошибки аппроксимации используются регрессионная и остаточная сумма квадратов.
Эти величины являются мерами разброса данных относительно среднего значения и линии регрессии.
Произведя расчет системы уравнений (1) и сравнив значения избыточных переменных с вычисленными значениями, можно судить о наличии ошибок, их локализации, а затем выполнить процедуры по их уменьшению.
Процедура обнаружения грубых ошибок сводится к проверке статистической гипотезы: невязка расчетных и измеренных значений должна принадлежать выборке среднеквадратического отклонения от регрессионной линии для предшествующего момента времени. Если эта гипотеза не принимается, то значит измеренные значения содержат грубую ошибку.
Измерения, входящие в контрольные уравнения с относительно малой невязкой, для которой выполняются условие
![]() ,
, ![]() ,
,
объявляются достоверными, т.е. их точность считается соответствующей априорным представлениям.
Имея статистический ряд расчетных параметров для схемы (рис. 1), на основе линейной регрессии можно составить таблицу среднеквадратического отклонения и дисперсию выборки (таблица 1, 2).
На основании регрессионного анализа составляется ковариационная матрица погрешностей вектора измерений, которая определяет априорную погрешность вектора измерений. Обычно полагается, что ковариационная матрица Rv – диагональная, т.е. погрешности двух различных измерений некоррелированы.
Математическая задача оценивания состояния заключается в том, что по измеренным параметрам режима U и P определить такие значения модулей и фаз напряжений в узлах, при которых обеспечиваются минимальные отклонения измеренных значений параметров U от значений тех же параметров U(x), вычисленных при найденных модулях и фазах напряжений.
Таблица 1. Среднеквадратическое отклонение и дисперсия выборки параметров линий
| Линия | 4-2 | 4-5 | 4-10 | 10-4 |
| | _ | _ | _ | 10,87 |
| | _ | _ | _ | 118,11 |
| | _ | _ | _ | 2,2 |
| | _ | _ | _ | 4,85 |
| | 53,78 | 12,4 | 53,58 | _ |
| | 2892,07 | 153,75 | 2870,59 | _ |
Таблица 2. Среднеквадратическое отклонение и дисперсия выборки параметров узлов
| № узла | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| | 0,014 | 0,012 | 0,012 | 0,0081 | 0,0084 | 0,0092 | 0,0005 | 0,0009 | 0,0004 | 0 |
| | 0,00019 | 0,00014 | 0,00014 | 6,57E-05 | 6,9E4-05 | 8,47E-05 | 2,11E-07 | 8,3E-07 | 1,3E-07 | 0 |
| | 0,68 | 0,64 | 0,64 | 0,58 | 0,54 | 0,48 | 0,73 | 0,72 | 0,73 | 0,65 |
| | 0,47 | 0,41 | 0,41 | 0,34 | 0,3 | 0,23 | 0,53 | 0,51 | 0,53 | 0,42 |
| | 10,56 | 0 | 1,87 | 0,87 | 1,79 | 3,5 | 1,1 | 1,13 | 0,79 | 11,8 |
| | 111,66 | 0 | 3,51 | 0,78 | 3,2 | 12,29 | 1,21 | 1,28 | 0,61 | 139 |
| | 5,03 | 0 | 0,51 | 0,18 | 0,33 | 2,37 | 0,22 | 0,39 | 0,23 | 2,26 |
| | 25,35 | 0 | 0,26 | 0,032 | 0,11 | 5,64 | 0,048 | 0,15 | 0,05 | 5,1 |
Применение метода Ньютона при оценивании состояния с необработанной телеметрией приводит к грубому, а в некоторых случаях и невозможному определению режима работы электрической сети [2]. Вследствие этого для нахождения минимального отклонения наиболее часто используется критерий минимума сумм взвешенных квадратов отклонений измеренных значений от вычисленных, т.е. определяется минимум функции:
![]() , (3)
, (3)
где ![]() является вектором состояния,
является вектором состояния, ![]() - вектор нелинейных зависимостей, которыми могут быть УУР в форме баланса мощностей с контрольными уравнениями (ограничений в виде равенств), R– диагональная матрица, содержащая на диагонали дисперсии ошибок соответствующих измерений.
- вектор нелинейных зависимостей, которыми могут быть УУР в форме баланса мощностей с контрольными уравнениями (ограничений в виде равенств), R– диагональная матрица, содержащая на диагонали дисперсии ошибок соответствующих измерений.
Соответственно величины ![]() выступают как весовые коэффициенты при слагаемых в критерии (3). В состав слагаемых критерия F следует вводить данные только тех измерений, для которых
выступают как весовые коэффициенты при слагаемых в критерии (3). В состав слагаемых критерия F следует вводить данные только тех измерений, для которых ![]() .
.
Имея сбалансированный режим по телеизмерениям узлов 1 и 6, справедливо утверждение, что, ![]()
![]()
![]()
![]() а значит, в состав критерия весовые коэффициенты для указанных измерений вводиться не будут.
а значит, в состав критерия весовые коэффициенты для указанных измерений вводиться не будут.
В то же время необходимо корректировать дорасчетные измерения мощности ненаблюдаемых узлов 3, 4 и расчетного узла 5 для которых ![]() . В соответствии с этим для решения поставленной задачи главная диагональ матрицы весовых коэффициентов при минимизации функции методом наименьших квадратов без применения контрольных уравнений будет иметь ряд:
. В соответствии с этим для решения поставленной задачи главная диагональ матрицы весовых коэффициентов при минимизации функции методом наименьших квадратов без применения контрольных уравнений будет иметь ряд:
![]()
Тогда задача ![]() при ограничении
при ограничении ![]() является типичной задачей нелинейного программирования
является типичной задачей нелинейного программирования
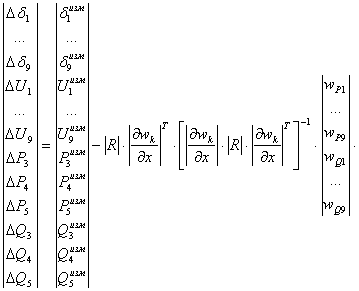
При добавлении контрольных уравнений для параметров I4-2, I4-5, I4-10, P10-4, Q10-4, главная диагональ матрицы весовых коэффициентов имеет ряд:
![]()
В этом случае задача нелинейного программирования сводится к решению уравнения:
 (4)
(4)
где
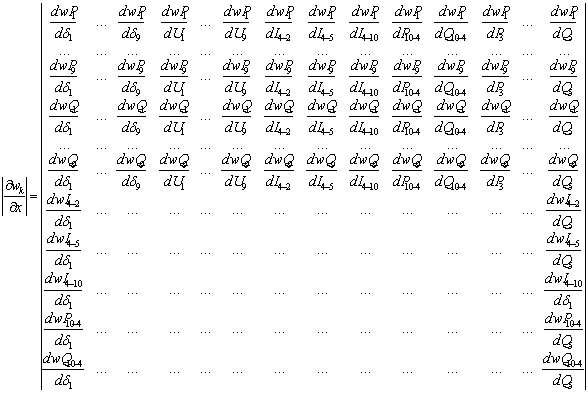
Результаты небалансов пяти итераций для уравнений установившегося режима и контрольных уравнений приведены в таблицах 3, 4.
В результате расчетов решается задача сглаживания ошибок измерений (фильтрация). Именно эта задача называется оцениванием состояния, включающая в себя обнаружение грубых ошибок.
Таблица 3. Небалансы уравнений установившегося режима
| Параметр/№ узла | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| wP I итерация | 0,1395 | -0,1179 | 1,0206 | 0,0123 | 0,004 | 0,0007 | 0,0035 | 0,0415 | 0,0033 |
| wP II итерация | -0,0027 | -0,2242 | 0,0231 | 0,0004 | 0,0001 | 0 | 0 | 0 | 0 |
| wP III итерация | 0,0012 | 0,0376 | 0,0192 | 0,0001 | 0 | 0 | 0 | 0 | 0 |
| wP I Vитерация | 0,0001 | 0,0056 | -0,0004 | 0 | 0 | 0 | 0 | 0 | 0 |
| wP V итерация | 0 | 0,0004 | -0,0002 | 0 | 0 | 0 | 0 | 0 | 0 |
| wQ I итерация | 0,051 | 0,5446 | -0,3739 | 0,0107 | 0,001 | 0,0008 | 0,0052 | 0,0511 | 0,0046 |
| wQ II итерация | -0,0002 | -0,144 | -0,0375 | 0,0008 | 0 | 0 | 0 | 0 | 0 |
| wQ III итерация | -0,0007 | -0,0345 | 0,0095 | 0,0001 | 0 | 0 | 0 | 0 | 0 |
| wQ IV итерация | 0 | 0,0057 | 0,003 | 0 | 0 | 0 | 0 | 0 | 0 |
| wQ V итерация | 0 | -0,0009 | 0,0005 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 4. Небалансы контрольных уравнений
| Итерация /Параметр | wI4--2 | wI4--5 | wI4--10 | wP10--4 | wQ10--4 |
| I итерация | -0,0067 | -0,0135 | -0,0189 | -0,0152 | 0,2686 |
| II итерация | -0,0105 | 0,0019 | -0,0011 | 0,0116 | 0,0153 |
| III итерация | 0,0022 | -0,0004 | 0 | -0,0022 | 0,0013 |
| IV итерация | -0,0004 | 0,0001 | 0 | 0,0005 | -0,0001 |
| V итерация | 0 | 0 | 0 | 0,0001 | 0 |
Перерывы или ограничения электроснабжения возможны при перегрузке отдельных элементов ЛЭП и трансформаторов, что определяет надежность электроснабжения потребителей. Увеличение тока, либо снижение напряжения за установленные пределы могут вызвать внезапное отключение противоаварийной автоматикой или ограничение нагрузки потребителя по указанию диспетчера. Контроль режима линий в реальном масштабе времени позволяет своевременно принять меры и предупредить аварийную ситуацию. При решении этой задачи для модели на рисунке (1) следует отметить параметры, контроль которых позволяет решить задачу определения статической устойчивости для транзитных линий и контроля напряжения узлов электрической системы:
I1-2, I4-2, I4-5, I6-5, I4-10, P10, Q10, U1, U4, U10 ,
где контрольные уравнения для I1-2, I4-2, I4-5, I6-5, I4-10 уже определены, а для корректировки параметров P10, Q10 базисного узла применяются УУН в форме балансов мощностей:
 (5)
(5)
 (6)
(6)
Узлы 1, 6 имеют сбалансированные значения мощностей, что означает примерное равенство нулю дисперсий ошибок измерений и поэтому в дальнейшем I1-2, I6-5, при анализе режима рассматриваться не будут.
В течение суток с интервалом в 12 минут проведена выборка ретроспективы телеизмерений. В каждый момент времени произведен расчет режима электрической системы методами Ньютона, квадратичной минимизации функции с применением весовых коэффициентов для мощностей узлов P3, P4, P5, Q3, Q4, Q5 и квадратичной минимизации, с применением контрольных уравнений для I4-2, I4-5, I4-10,, P10, Q10.Дисперсии ошибок соответствующих измерений (весовые коэффициенты) найдены по вышеприведенной методике.
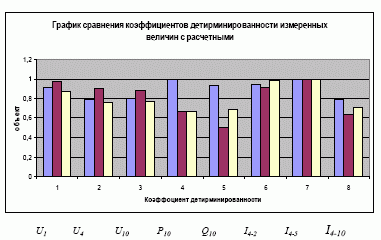
Анализ измеренных и расчетных параметров производится на основе коэффициента детерминированности r2 (рис.3) и F-статистики (табл. 5).
Коэффициент детерминированности показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, описывает фактические данные.
Коэффициент детерминированности может принимать значения от 0 до 1, причем 1 соответствует полному совпадению прогнозируемых и фактических данных. Хорошим приближением считается такое, при котором значение коэффициента больше 0,9.
F-статистика используется совместно с F-значениями для определения вероятности того, что данные действительно описываются указанным выражением или совпадение вызвано случайными флуктуациями.
![]() - Минимизация функции методом наименьших квадратов с применением весовых коэффициентов и контрольных уравнений.
- Минимизация функции методом наименьших квадратов с применением весовых коэффициентов и контрольных уравнений.
![]() - Минимизация функции методом наименьших квадратов с применением весовых коэффициентов без контрольных уравнений.
- Минимизация функции методом наименьших квадратов с применением весовых коэффициентов без контрольных уравнений.
![]() - Расчет методом Ньютона.
- Расчет методом Ньютона.
Рис. 3. Сравнение коэффициентов детерминированности измеренных величин с расчетными
Таблица 5. F-статистика ранее основных параметров электрической системы
|
| Метод расчета | ||
| Наименование параметра и объекта | Метод Ньютона | Метод наименьших квадратов с применением весовых коэффициентов | Метод наименьших квадратов с применением весовых коэффициентов и контрольных уравнений |
| F-статистика U1 | 153 | 784,7 | 250,3 |
| F-статистика U4 | 70,4 | 233,8 | 87 |
| F-статистика U6 | 75,5 | 180,4 | 94,5 |
| F-статистика P10 | 45,9 | 45,9 | 117818,8 |
| F-статистика Q10 | 23 | 23,1 | 308,6 |
| F-статистика I4-2 | 1775,1 | 245,9 | 374,2 |
| F-статистика I4-5 | 31622,5 | 5249 | 9165,9 |
| F-статистика I4-10 | 56,6 | 41,6 | 90,2 |
| F-статистика табл. | 4,27 | ||
Анализируя данные рисунка 3 можно отметить, что параметры P10 и Q10 имеют малое значение коэффициента детерминированности в случае расчета режима по методу Ньютона и минимизации методом наименьших квадратов без применения контрольных уравнений. Это говорит о неточном описании уравнения регрессионного анализа фактических данных, что и надо было бы предполагать из-за того, что узел 10 является базисным и в этом случае расчетные значения мощности этого узла включают в себя погрешности измерений всех узлов электрической схемы. Добавление контрольных уравнений (2, 5, 6) позволяет более точно рассчитать эти параметры вследствие того, что ошибки измерений распределяются между узлами в зависимости от значения весового коэффициента заданного для каждого параметра.
Ранее рассматривалось соответствие весовых коэффициентов при статистическом анализе за прошедший период времени. В дальнейшем приводится анализ применения весовых коэффициентов в реальном масштабе времени на основе рассмотрения коэффициента детерминированности и F - статистики.
По вышеприведенной методике производится сравнение расчетных режимных параметров реального времени, с применением весовых коэффициентов, полученных в результате регрессионного анализа:
· с интервалом в один час за предыдущие сутки;
· во время контрольного замера за два месяца до времени измерения;
В таблице 6 приведены значения весовых коэффициентов для перечисленных случаев.
Таблица 6. Значения весовых коэффициентов
| | U1 | U4 | U6 | P10 | Q10 | I4-1 | I4-5 | I4-10 |
| | 2,85 | 2,28 | 2,06 | 0,03 | 5,35 | 547 | 5064 | 1152 |
| | 1,59 | 1,73 | 1,85 | 0,13 | 5,4 | 3301 | 60887 | 4042 |
При минимизации функции методом наименьших квадратов получены результаты коэффициента детерминированности (табл. 7) и F-статистики (табл. 8) для случаев с коэффициентами полученными за время предыдущих суток и по контрольному замеру относительно измеренных параметров реального времени.
Таблица 7. Коэффициенты детерминированности
|
| Метод расчета | |
| Наименование параметра и объекта | Метод наименьших квадратов с применением весовых коэффициентов вычисленных во время предыдущих суток | Метод наименьших квадратов с применением весовых коэффициентов вычисленных во время контрольного замера |
| r2 U1 | 0,889352524 | 0,87507 |
| r2 U4 | 0,695968925 | 0,712728 |
| r2 U6 | 0,716275096 | 0,502085 |
| r2 P10 | 0,999999867 | 0,900669 |
| r2 Q10 | 0,991109903 | 0,592977 |
| r2 I4-2 | 0,919463165 | 0,94425 |
| r2 I4-5 | 0,999114172 | 0,999054 |
| r2 I4-10 | 0,972086007 | 0,979682 |
Таблица 8. F-статистика
|
| Метод расчета | |
| Наименование параметра и объекта | Метод наименьших квадратов с применением весовых коэффициентов вычисленных во время предыдущих суток | Метод наименьших квадратов с применением весовых коэффициентов вычисленных во время контрольного замера |
| F-статистика U1 | 184,867372 | 161,10312 |
| F-статистика U4 | 52,6501616 | 57,063428 |
| F-статистика U6 | 58,0644384 | 23,192586 |
| F-статистика P10 | 173423640 | 208,54888 |
| F-статистика Q10 | 2564,14828 | 23 |
| F-статистика I4-2 | 262,583608 | 389,55945 |
| F-статистика I4-5 | 25941,3946 | 24284,462 |
| F-статистика I4-10 | 800,959507 | 1109,0166 |
| F-статистика табл. | 4,27 | |
Коэффициенты детерминированности при весовых коэффициентах за предыдущие сутки имеют большее значение, чем при коэффициентах доверия контрольного замера и в основном имеют величину больше 0,9. Кроме того по данным F- статистики (таблица 8) видно, что параметры P10 и Q10 имеют не только большее значение в первом случае по сравнению со вторым, но и превышают на несколько порядков.
На основе этого можно сделать вывод, что весовые коэффициенты, вычисленные за время предыдущих суток, лучше описывают значения измерений в реальном масштабе времени, чем коэффициенты, полученные во время контрольного замера. Применение контрольных уравнений для параметров I1-2, I4-2, I4-5, I6-5, I4-10, P10, Q10 позволяет максимально приблизить значения расчетных величин к измеренным и оптимально распределить ошибки измерений по всем узлам электрической системы в соответствии с коэффициентом доверия для каждого параметра в узлах схемы.
При сравнении методов расчета можно сказать, что количество итераций увеличивается при применении контрольных уравнений, но при этом увеличивается точность рассчитанных параметров электрической системы.
СПИСОК ЛИТЕРАТУРЫ:
- Гамм А.З., Гришин Ю.А., Окин А.А. Развитие АСДУ ЕЭС с учетом новых условий и механизмов управления. Энергетика России в переходный период: проблемы и научные основы развития и управления. - Новосибирск, Наука, 1996.
- Фундаментальные исследования. № 9 2006 г. Москва. Международная научная конференция 1-8 октября 2006 г. Греция (Лутраки). “Анализ надежности электроэнергетических систем с исходными данными телеметрии”. Ярцев С.Д.



