Описываемые результаты являются продолжением исследований в области формообразования и раскроя тентовых покрытий из плоских заготовок [6]. Разработанные авторами методы расчета раскроя оболочек с учетом перестройки сетевой структуры материалов, приведенные в работах [5], показывают теоретическую возможность покрытия плоскими раскройными сетевыми элементами поверхностей различной геометрии. В качестве примера на рис. 1 приводится форма вычисленного авторами плоского раскроя сферической оболочки.
Часто используемыми геометрическими формами тентовых оболочек являются поверхности, образованные вращением вогнутых кривых вокруг вертикальной оси, известные как шатровые тенты. Раскрой таких поверхностей традиционно проводится в виде набора большого количества клиновидных элементов, ограниченных смежными меридианами. Такой подход имеет ряд нежелательных результатов, таких как перерасход материалов, образование складок и перекосов в швах тентового сооружения из-за неравномерности двухосного напряженного состояния.
Основной целью исследования является разработка методики раскроя шатровых тентовых покрытий, основанной на применении сетей с равносторонними ячейками и представлении формы оболочки вращения отрицательной кривизны как сочетания седловых поверхностей, ориентированных и состыкованных по кратчайшим линиям.
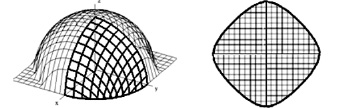
Рис. 1. Раскрой полусферы. Слева – фрагмент сети Чебышева на сфере. Справа – плоский раскрой половины сферы
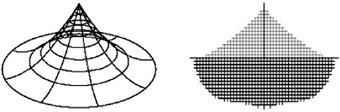
Рис. 2. Пример плоского раскроя половины поверхности шатра. Слева – общий вид шатра
Первая попытка традиционного формообразования шатровых оболочек из плоских раскройных элементов, но с учетом структурной перестройки материала и использования сетей Чебышева, описанная авторами в работе [1], носила характер расчетного эксперимента. В качества примера авторы рассчитали форму плоской заготовки половины поверхности шатровой оболочки с вогнутыми параболическими образующими. Результаты расчета приведены на рис. 2. Как показали расчеты, реальное использование для целей раскроя оболочек сетей с равносторонними ячейками, называемыми сетями Чебышёва, хорошо моделирующими свойства тентовых материалов имеет серьёзные ограничения. Они связанны с малой изменяемостью углов между нитями арматуры при деформациях тканево-сетчатой структуры тентовых материалов.
Проведенные авторами исследования [3] подтверждают, что изменения сетевых углов армирующей основы без образования складок в материале обычно не превышают шести градусов. В связи с этим раскрой тентовых оболочек требует определения границ участков, которые могут быть покрыты изначально плоскими заготовками в допустимых пределах изменения сетевых углов при формообразовании.
Для оболочек отрицательной гауссовой кривизны характерна седловидная форма поверхности. В связи с этим авторы предлагают представить шатер в виде набора «седловых поверхностей», иногда в обиходе называемых «гипарами» по внешней аналогии с формой гиперболического параболоида. В качестве примера такого представления на рис. 3 приводится схема шатра, составленного из двух типоразмеров элементов седловидной формы.
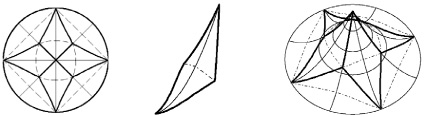
Рис. 3. Пример сборки шатра из седловых элементов (показан в центре) по кратчайшим линиям на поверхности. Слева – вид сверху, справа – в аксонометрии
Для реализации предлагаемой схемы компоновки тентовой оболочки требуется решить задачу вычисления положений основных осей и границ стыковки элементов. Заметим, что ортогональность армирования материала оболочек предполагает взаимную ортогональность осей раскройных элементов. Следует особо отметить, что оси элементов как направления основного силового натяжения стремятся располагаться вдоль кратчайших линий на поверхностях. В связи с этим возникает задача построения кратчайших линий на шатрах, форма которых характеризуется отрицательной гауссовой кривизной. Из теории кратчайших линий [2] известно, что ими являются образующие оболочки вращения, что предполагает размещение одной из осей элемента вдоль образующих. Вторая ось элемента должна быть перпендикулярной к ней. Линии стыковки раскройных элементов также желательно направить по кратчайшим линиям для минимизации длины швов и устранения деформаций перекосов, или складок, на границах седловых элементов.
Для построения кратчайших линий на поверхностях вращения предлагается использовать теорему Клеро. Она доказывает, что во всех точках кратчайшей линии, как показано на левой схеме рис. 4, произведение радиуса параллели на синус угла между геодезической линией и меридианом – величина постоянная (1).
r∙sin α = c = const. (1)
Если заменить угол α, на угол β – угол между геодезической и параллелью, то формула примет вид (1а)
r∙cos β = c = const. (1а)
Такой подход позволяет, задавшись координатами начала и конца линии и одним из углов между геодезической и параллелью или меридианом, построить кратчайшую линию между двумя точками на поверхности шатра.
Авторами разработан и программно реализован алгоритм численного способа построения кратчайших линий на шатровых оболочках. Суть его заключается в нахождении координат узлов линии из прямолинейных отрезков малой длины, направление каждого из которых соответствует правилу (1а). Схемы, поясняющие алгоритм, приведены на рис. 4.
Исходными данными для расчета являются:
zi = f(ri) – уравнение образующей;
d – длина малого прямолинейного отрезка искомой кратчайшей линии;
r0, rk – радиусы параллелей в начальной и конечной точках;
cos (βk) – косинус угла линии с параллелью в конечной точке;
γk – угол между образующими в начальной и конечной точках.
Ниже приняты следующие обозначения:
xi, yi, zi – координаты текущего искомого узла линии;
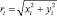– радиус параллели в текущем узле кратчайшей линии;
αi, βi – текущие углы кратчайшей с меридианом и параллелью соответственно.
Алгоритм расчета
Разработанный авторами алгоритм включает выполнение нескольких последовательных процедур:
1. Вычисление текущего значения косинуса угла линии с параллелью расчетной точке на основе теоремы Клеро по формуле (2)
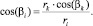(2)
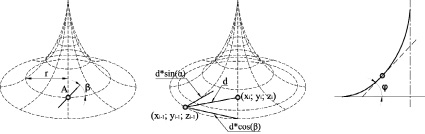
Рис. 4. Схемы к вычислению координат узлов кратчайших линий на поверхности вращения. Слева – схема к теореме Клеро. В центре – к формуле (2). Справа – к формуле (4)
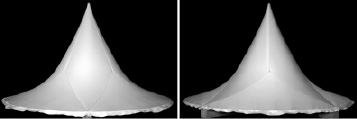
Рис. 5. Фото модели шатра, спроектированного с применением предлагаемых принципов раскроя и алгоритма расчета
2. Определение по соотношению (3) нового значения угла до текущего меридиана, на котором находится следующий узел кратчайшей линии:
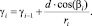(3)
3. Вычисление радиуса параллели нового узла, по проекции участка линии на плоскость параллели:
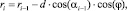(4)
где
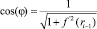
и
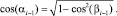
4. Вычисление декартовых координат искомого узла по формулам (5)
xi = d∙cos (γi); yi = d∙sin (γi); zi = f(xi, yi). (5)
Примеры линий, построенных по приведенному алгоритму, приведены на рис. 3.
В порядке эксперимента алгоритм расчета был использован при расчете раскроя модели шатровой оболочки, изготовленной авторами. Фотографии модели представлены на рис. 5. На них видны седловидные участки, образованные из плоских раскройных элементов, ориентированных и состыкованных по кратчайшим линиям на поверхности, рассчитанным по описанному выше алгоритму.
Выводы
Экспериментальные расчеты и модельные исследования показали реальную возможность представления шатровой оболочки как поверхности вращения отрицательной кривизны в виде набора седловидных элементов, границы которых могут определяться по предлагаемому алгоритму построения кратчайших линий для целей проектирования шатровых тентовых оболочек.
Рецензенты:
Куприянов В.Н., д.т.н., профессор, зав. кафедрой «Проектирование зданий», Казанский государственный архитектурно-строительный университет, г. Казань;
Ахмадиев Ф.Г., д.т.н., профессор, зав. кафедрой «Прикладная математика», Казанский государственный архитектурно-строительный университет, г. Казань.