«Физика без теории, что математика
без доказательств - аксиома».
Запишем уравнение, содержащее неизвестное под знаком модуля.
│F│ = 0 (1),
где F – неизвестный модуль силы.
В уравнении (1) существует единственное число, модуль которого равен нулю, это число 0, то есть F = 0 (2) единственный корень уравнения. Однако математики ошибаются, уравнение (1) имеет два корня уравнения.
Запишем неизвестное так
0,5 F + 0,5 F = F, (3)
где
F1 = F2 = F, (4)
тогда уравнение (3) будет иметь вид:
0,5 F1 + 0,5 F2 = F, (5)
а уравнение (1) запишется так:
│0,5 F1 + 0,5 F2 │ = │F│ = 0, (6)
откуда
0,5 F1 + 0,5 F2 = 0 (7)
или
0,5 F1 = - 0,5 F2. (8)
Уравнение (8) - это неравенство, потому что
0,5 ≠ - 0,5 (9) и F1 ≠ - F2. (10)
Приведем уравнение (5) к общему знаменателю, получим:
F1 + F2 = 2 F (11)
Уравнение (11) это закон сохранения импульса тел. При ударе
F = 0 (12)
Уравнение (11) будет иметь вид
F1 = - F2 (13)
Уравнение (13) это третий закон Ньютона, выведенный теоретически из закона сохранения импульса тел.
Взаимодействие двух тел всегда порождает пару сил F1 и F2 , которые действуют друг на друга, равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти тела.
Согласно определению третьего закона Ньютона уравнение математически запишется так
F1 = F2 Cos 180o, (14)
откуда F1 = - F2
Следует отметить, что сила F1 – это сила, с которой второе тело действует на первое, она приложена к первому телу. F2 – сила, с которой первое тело действует на второе.
Эта сила приложена ко второму телу, поэтому эти силы не уравновешивают друг друга и их нельзя складывать.
Уравнение (10) может стать равенством, но только по модулю
F1 =| - F2, |, (15)
откуда F1 = - F2 – векторное равенство, F1 = F2 (16) – равенство по модулю.
Из уравнения (16) вытекает следствие: уравнения, связанные с третьим законом Ньютона содержат неизвестное под знаком модуля.
Рассмотрим практическое применение вывода в физике, например, в законе всемирного тяготения (см. рис. 1).
, (17)
где m1 и m2 – масса тел,
r – расстояние между центрами тел,
γ - гравитационная постоянная,
F – сила тяготения.
Рис. 1.
Так как закон всемирного тяготения связан с третьим законом Ньютона, то согласно следствию уравнение (17) будет иметь вид:
(18)
откуда
(19)
(20)
Если правые части равенств (19) и (20) равны по модулю, равны и левые, откуда
F1 = - F2,
а это и есть третий закон Ньютона, выведенный из закона всемирного тяготения.
Уравнение (20) можно представить так: 
где F r = Eп – потенциальная энергия гравитационного поля. Вывод этой формулы довольно громоздкий §1.
Рассмотрим тему: «Давление газа на стенки сосуда на примере одной молекулы идеального газа».
Пусть υ её скорость, направленная перпендикулярно к стенке сосуда, а m - масса. При упругом ударе молекула сообщает стенке импульс m υ.
Следовательно, импульс молекулы изменится на
m υ - (-m υ) = 2 m υ (22)
По второму закону Ньютона
F1 t = 2 m υ § 2. (23)
Согласно закона сохранения импульса: импульс до взаимодействия тел равен импульсу после взаимодействия. Но mυ ≠ 2 mυ, т.е нарушается третий закон Ньютона F1 ≠ 2 F1 (см. рис. 2.), а соответственно - и закон сохранения импульса тел.
Наш вариант решения:
Запишем уравнение (11) в таком виде F1 t + F2t = 2 F t (24), где F t = mυ (25). До взаимодействия молекулы со стенкой F2 t = 0 (26), тогда F1 t = 2 mυ (27). После действия стенки на, молекулу F1 t = 0 (28), уравнение (24) запишется так F2 t = 2 mυ (29) (см. рис. 3).
Согласно закона сохранения импульса: импульс до взаимодействия тел равен импульсу после взаимодействия.
импульс после взаимодействия
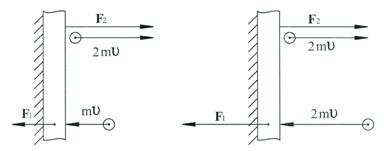
импульс до взаимодействия тел
Рис. 2 Рис. 3
Мы привели только два примера неверных теорий, а их существует гораздо больше, например, закон Кулона, капиллярные явления, теорема Гаусса, и т.д.
Резюме:
- Теоретически доказан закон сохранения импульса тел, не совпадающий с общепринятым из которого, как частный случай, выводится третий закон Ньютона. § 3. с. 30.
- Уравнение вида | F | = 0, содержащее: неизвестное под знаком модуля, имеет не единственный корень уравнения, как утверждают математики, а два.
- Теоретический вывод третьего закона Ньютона потребует пересмотра теории всей классической физики.
СПИСОК ЛИТЕРАТУРЫ:
- § 1, § 2, § 3 Дмитриева В.Ф., Прокофьев В.Л. Основы физики. – М.: Высшая школа, 2001. с. 46-48, с.94, с. 30.