STRUCTURAL DYNAMIC MODELS OF MONOGALOIDYS SUBSTITUTED SIX-MEMBERED CYCLIC COMPOUNDS IN THE CONDENSED STATE

Согласно современным научным воззрениям основные физико-химические свойства молекулярных объектов определяются формой их адиабатического потенциала. Под адиабатическим потенциалом в квантовой механике молекул принято считать результат решения квантового уравнения для электронной подсистемы исследуемого соединения [1]. Аналитическое решение такого уравнения не представляется возможным, что и привело к появлению упрощенных квантовых моделей для ансамбля электронов молекулярной системы. Созданные модели и стали основой такого известного научного направления в теории строения молекул, как квантовая химия, синонимом которой является квантовая теория молекул. В ней речь идет об использовании квантовой химии для построения структурно-динамических моделей молекулярных объектов, предсказания их конформационных и оптических свойств, спектроскопической интерпретации эксперимента по спектрам инфракрасного поглощения и комбинационного рассеяния.

Построение структурно-динамических моделей молекулярных соединений является одной из задач такого зародившегося современного научного направления, как молекулярное моделирование. Основы молекулярного моделирования заложены результатами хорошо развитой классической теории колебаний многоатомных молекул. Оценка гармонических параметров адиабатического потенциала молекулярных соединений различных классов базировалась на решении обратных спектральных задач. Для этого требовалось наличие полной информации по экспериментальным данным в спектрах ИК и КР и исходное нулевое поле силовых констант для исследуемого соединения. За подробностями отсылаем к широко известной в мировой науке монографии [2]. В монографии представлена обширная база данных по экспериментальной и теоретической интерпретации фундаментальных колебаний обширного списка соединений, их геометрии из рентгеноструктурного и электронографического эксперимента. Приведены и оценочные данные по гармоническим силовым константам (гармоническим параметрам адиабатического потенциала) для ряда молекулярных фрагментов.

Решение обратных спектральных задач требует наличия экспериментальной интерпретации спектра фундаментальных колебаний для изотопозамещенных аналогов исследуемого молекулярного объекта. Выбор же исходного приближения для системы гармонических силовых констант, варьирование которой до хорошего совпадения результатов теоретических расчетов колебательных состояний с данными эксперимента, требовал физического обоснования. Таковым была схема переноса гармонических силовых констант из родственных по электронной структуре молекулярных фрагментов.

Наглядным примером может служить теоретическая интерпретация колебательного спектра для шестичленных азациклов (пиридина, пиримидина, пиразина, пиридазина, триазина, тетразина), предложенная в монографии [2] на основании критического обзора соответствующей периодической литературы, вызванного расхождением в оценках частот фундаментальных колебаний азациклических соединений по данным эксперимента в ИК и КР спектрах. В качестве исходного силового поля использовались оценки гармонических силовых констант для молекулы бензола. Здесь известной трудностью являлась неоднозначность в выборе знака переносимых значений недиагональных силовых констант.

Имеющие известные недостатки классического подхода в оценке параметров адиабатического потенциала молекулярных соединений [2] послужили основанием для применения квантово-химических методов в обосновании полученных результатов. Исторически таковыми сначала являлись полуэмпирические методы, с помощью которых можно было устранить возникающие разногласия в схеме переноса гармонических силовых постоянных.

Активное развитие неэмпирических и гибридных квантовых методов молекулярной физики для исследования формы адиабатического потенциала, компьютерная реализация указанных методов в виде сервисных информационных технологий стали основой современного молекулярного моделирования. Появилась реальная возможность осуществления предсказательных расчетов структуры и спектров сложных молекулярных соединений в свободном и конденсированном состояниях, выявления признаков спектроскопической идентификации позиционных таутомеров и их возможных конформеров для исследуемого класса соединений, оценки значений гармонических и ангармонических параметров адиабатического потенциала. Квантовые методы стали использовать для устранения имеющихся разногласий в интерпретации колебательных спектров ряда молекулярных соединений, полученных в рамках классической схемы. К таковым в первую очередь следует отнести соединения химического промышленного производства. Для примера сошлемся на интерпретацию спектров карбоновых кислот [4]. Квантовые методы моделирования адиабатических параметров позволили приступить к теоретической интерпретации молекулярных объектов, для которых классический подход не может быть применен хотя бы ввиду отсутствия полного экспериментального исследования полос изотопозамещенных аналогов в ИК и КР спектрах и надежной интерпретации спектров отдельных фрагментов, входящих в состав исследуемого соединения. В качестве примера сошлемся на такие известные природные соединения, как гидроксизамещенные флавона – флавоноиды [3]. Возможность построения структурно-динамических моделей наиболее значимых представителей указанного класса соединений продемонстрирована в публикациях [5–6].

Однако квантовый подход в оценке параметров адиабатического потенциала сложных молекулярных объектов и построение их структурно-динамических моделей требует обоснования достоверности получаемых результатов.

Основным аргументом принято считать хорошее совпадение результатов теоретической интерпретации колебательных спектров исследуемого объекта с имеющимися в наличии экспериментальными данными по спектрам ИК и КР. Дополнительными можно считать факт воспроизводства низкочастотных колебаний (колебаний внутреннего вращения [2]) и характер поведения параметров полос в различных спектральных диапазонах. В этом случае можно сделать выводы о конформационных особенностях молекулярной геометрии и взаимном влиянии силовых полей отдельных молекулярных фрагментов.

В данной публикации продемонстрируем схему возможности обоснования доверительности предсказательных модельных квантовых оценок параметров адиабатического потенциала и предлагаемой на их основе интерпретации спектра фундаментальных колебаний моногалоидозамещенных шестичленных циклических соединений.

Модельные квантовые расчеты и их обсуждение

Модельные квантовые расчеты параметров адиабатического потенциала моногалоидозамещенных бензола, бензохинона, гамма-пирона и тиопирона (рисунок) осуществлялись в рамках метода функционала плотности DFT/b3LYP с использованием базисных наборов 6-311G** b 6-311+** [10]. Такой подход позволил констатировать, что выбор базиса не имеет принципиального значения для построения структурно-динамических моделей указанных галоидозамещенных шестичленных циклических соединений. Смещение положения полос не превышает величины ~ 10 см–1, качественная оценка интенсивностей сохраняется.

Диапазоны изменения расчетных значений геометрических параметров шестичленного фрагмента в монозамещенных (в том числе и галоидозамещенных) бензола, бензохинона, гамма-пирона и тиопирона представлены в табл. 1. Эти данные дают основание констатировать, что изменение геометрических параметров по отношению к значениям длин валентных связей и валентных углов носит локальный характер.

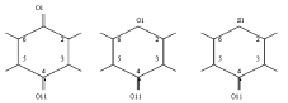
pic_12.tif

Нумерация атомов в бензохиноне, 4-гамма-пироне 4-тиопироне

Таблица 1

Расчетные значения геометрических параметров (ГП) монозамещенных бензола (МЗБ), бензохинона (МЗБХ), гамма-пирона (МЗГП) и тиопирона (МЗТП)

ГП	МЗБ	МЗБХ	МЗГП	МЗТП	ГП	МЗБ	МЗБХ	МЗГП	МЗТП
R (1, 2)	1,39	1,50	1,34–1,36	1,72–1,75	A (2, 3, 8)	118	121–122	115–120	118–119
R (1, 6)	1,40	1,49	1,35–1,37	1,74	A (4, 3, 8)	122	116	119–126	115–124
R (2, 3)	1,39	1,34	1,34–1,35	1,35–1,36	A (3, 4, 5)	121	117	112–113	116–117
R (3, 4)	1,40	1,49	1,47–1,49	1,47–1,49	A (3, 4, 11)	120	121	123–126	121–124
R (4, 5)	1,40	1,48	1,47	1,46–1,48	A (5, 4, 11)	120	122	122–124	119–122
R (5, 6)	1,39	1,34	1,34	1,34–1,35	A (4, 5, 6)	122	121	121–122	125–125
A (2, 1, 6)	120	117	118	100–101	A (4, 5, 9)	118	116	118–119	114–116
A (1, 2, 3)	120	120	123–125	125–127	A (6, 5, 9)	120	123	120	119
A (1, 2, 7)	118	119–123	111–115	112–117	A (1, 6, 5)	119	122–123	123–124	125–127
A (3, 2, 7)	122	117–121	122–126	119–123	A (1, 6, 10)	121	115	111	112–113
A (2, 3, 4)	120	122–123	120–121	123–126	A (5, 6, 10)	120	123	125	121–122

Примечание. Длины валентных связей R(i, i) в Å, значения валентных углов в A(i, j, k) в град.

В табл. 2–5 предложена интерпретация спектра фундаментальных колебаний бензола, бензохинона, гамма-пирона и тиопирона на основании квантовых оценок параметров адиабатического потенциала.

Таблица 2

Интерпретация спектра фундаментальных колебаний галоидозамещенных бензола

Форма колебаний	С6Н5D		С6Н5F				С6Н5Cl				С6Н5Br
Форма колебаний	νэкс	νвыч	νэкс	νвыч	ИК	КР	νэкс	νвыч	ИК	КР	νэкс	νвыч	ИК	КР
Q, β, γ	1591	1591	1603	1602	10	9	1583	1586	3	7	1585	1582	2	7
Q, β, γ	1574	1574	1595	1598	46	8	1580	1582	25	15	1577	1577	26	15
β, Q	1480	1480	1496	1487	80	1	1479	1471	47	0	1475	1467	42	0
β, Q	1450	1450	1460	1450	2	0	1443	1440	7	1	1441	1437	8	1
β, Q	–	1321	1326	1311	0	0	1322	1310	0	1	1319	1309	1	1
β, Q	1292	1292	–	1290	0	1	1263	1286	0	0	1263	1284	0	1
qCX	2269	2263	1220	1221	93	9	1068	1071	41	12	1071	1057	20	7
β	1176	1176	1156	1151	0	2	1174	1169	0	2	1176	1171	0	3
β	1158	1158	1156	1147	13	7	1157	1154	0	4	1158	1155	0	4
β, Q	1076	1076	1065	1064	8	2	1083	1072	6	1	1068	1071	4	0
Q, β, γ	1031	1031	1021	1015	4	8	1024	1019	20	20	1020	1014	24	28
γ	1007	1007	1009	995	0	24	1002	992	6	24	1001	990	12	25
γ	980	980	806	805	26	13	702	692	29	5	673	666	22	4
γ	601	606	613	615	0	5	615	615	0	4	614	614	0	4
γ	603	601	519	514	5	4	418	405	5	8	315	307	2	7
βCX	858	858	407	396	2	0	279	292	0	1	254	245	0	1
ρ, χ	995	995	997	968	0	0	987	980	0	0	990	979	0	0
ρ, χ	970	970	970	949	0	0	965	956	0	0	964	955	0	0
ρ, χ	922	922	896	886	8	1	903	896	2	0	905	897	2	0
ρ	849	849	818	813	0	1	830	822	0	1	832	824	0	1
ρ, χ	775	775	754	751	75	0	740	737	58	1	737	733	62	1
χ, ρ	698	698	687	682	17	0	682	688	25	0	681	686	19	0
ρCX, χ	608	608	519	501	10	0	470	470	11	0	460	459	9	0
χ	405	405	407	416	0	0	418	409	0	0	409	406	0	0
χ	380	380	242	235	0	4	196	184	0	2	181	164	0	3

Примечание. Частоты колебаний ν в см–1, интенсивности в спектрах ИК в моль/км, в спектрах КР в Å4/а.е.м.

Теоретическая оценка положения полос в колебательном спектре соединения осуществлялась с помощью известного соотношения ангармонической теории молекулярных колебаний:

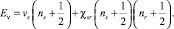elkin01.wmf (1)

Для ангармонических констант χsr использованы выражения из публикации [8]:

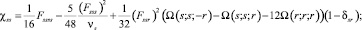elkin02.wmf (2)

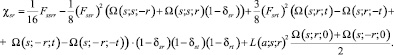elkin03.wmf (3)

Отметим, что ангармоническое смещение полос, полученное с использованием приведенных соотношений, хорошо согласуется с результатами применения процедуры масштабирования типа [7]

ν_анг = (0,98 – 4,4Е – 0,6 νг) νг. (4)

Максимальное расхождение не превышает величины Δν ~ 20 см–1.

Для моногалоидозамещенных бензола (табл. 2) предложенная интерпретация спектра фундаментальных колебаний хорошо согласуется с результатами реального эксперимента, описанного в монографии [2]. Сравнение с интерпретацией колебаний для монодейтеробензола (С6H5D) дает основание сделать вывод, что влияние галоидозамещения на силовое шестичленного цикла носит локальный характер, что проявляется в характеристичности положения полос в диапазоне выше 1000 см–1. Существенное различие в значениях частот колебаний в диапазоне ниже 1000 см–1 есть результат влияния кинематических параметров заместителя (массы атома и длины связи СХ). Это относится в первую очередь к плоским деформационным колебаниям валентных углов шестичленного цикла (γ) и углов ССХ (βСХ).

Отметим характеристичность по частоте и интенсивности полос, отнесенных к неплоским деформационным колебаниям (ρ, χ) связей бензольного цикла. Смещение полосы (ρCX), отнесенной к выходу связи С-Х (D, F,Cl, Br), определяется в основном кинематическими параметрами заместителя Х. Следует обратить внимание на низкую интенсивность полос неплоских колебаний в спектрах КР. В спектре ИК в диапазоне 800–770 см–1 значительной интенсивностью обладает полоса, отнесенная к неплоскому колебанию типа ρ,χ.

Таблица 3

Интерпретация спектра фундаментальных колебаний галоидозамещенных 1,4-бензохинона (БХ)

Форма колебаний	1,4-БХ		1,4-БХ (d1)		F-1,4-БХ			Cl-1,4-БХ			Br-1,4-БХ
Форма колебаний	νэкс	νвыч	νэкс	νвыч	νвыч	ИК	КР	νвыч	ИК	КР	νвыч	ИК	КР
Qc = o, γ	1686	1705	1679	1702	1711	225	100	1711	218	57	1707	219	43
Qc = o, γ	1686	1686	1664	1685	1691	178	151	1690	162	164	1688	159	168
Q, β, γ	1635	1630	–	1624	1659	55	20	1636	2	24	1635	1	20
Q, β, γ	1614	1600	1588	1589	1612	55	0	1591	92	20	1585	98	26
β, Q	1394	1359	1363	1356	1349	6	16	1347	6	14	1345	7	13
β, Q	1354	1354	1323	1307	1324	48	3	1286	19	6	1282	19	7
Q, β, γ	1299	1259	1284	1250	1261	59	12	1251	102	12	1245	115	14
qCX	3092	3094		2361	1178	77	1	972	133	1	951	109	1
β, Q	1211	1190	1201	1171	1150	30	20	1171	3	21	1170	4	22
β, Q	1147	1128	1100	1088	1071	94	9	1080	29	11	1075	41	12
γ, Q	942	933	962	956	874	13	3	828	19	3	804	13	2
γ, Q	770	752	765	746	770	1	1	763	1	2	760	1	3
γ	728	726	–	700	669	7	8	626	10	6	614	7	5
βC = O, γ,	599	588	595	581	584	4	3	547	11	4	525	10	3
γ, βC = O	447	448	–	447	471	3	6	457	5	10	453	4	11
γ, βC = O	447	443	445	435	428	8	4	422	20	2	419	25	1
γ, βC = O	409	405	407	404	385	13	1	335	2	2	260	1	3
βCX	1051	1057	875	859	301	0	1	227	0	3	183	0	3
ρ	996	1007	988	1002	996	0	0	999	0	0	999	0	0
ρ, χ	969	1000	933	949	888	75	0	907	53	0	909	52	0
ρ, χ	882	893	850	856	832	5	4	831	19	2	827	18	3
χ, ρC = O	793	785	792	783	761	0	6	772	0	5	770	0	5
χ, ρ	747	748	670	678	613	3	1	591	0	3	583	0	2
ρCХ,χ	505	508	474	478	404	0	0	386	2	0	375	1	0
χ	310	335	300	325	270	0	2	259	0	2	255	0	2
χ	244	228	238	224	170	2	1	149	3	1	139	3	1
χ	89	93	108	92	90	9	0	83	9	0	80	8	1

Для галоидозамещенных бензохинона не располагаем экспериментальными данными, поэтому интерпретация спектра фундаментальных колебаний моногалоидозамещенных аналогов бензохинона (табл. 3) носит предсказательный характер. Обоснованием достоверности представленных результатов могут служить закономерности в характере поведения полос при монозамещении. Для монодейтеробензохинона (1,4-БХ (d1)) имеем хорошее совпадение квантовых модельных расчетов спектра фундаментальных колебаний с данными из реального эксперимента [11, 12]. Характер смещения полос при монозамещении по отношению к спектру базовой молекулы (1,4-БХ) может служить обоснованием достоверности предлагаемой интерпретации спектра фундаментальных колебаний моногалоидобензопиронов.

Проявление свойства характеристичности полос по частоте в диапазоне выше 1000 см–1 дает основание сделать вывод о локальном влиянии заместителей на силовое поле шестичленного циклического фрагмента. Смещение полос в диапазоне ниже 1000 см–1 обусловлено влиянием кинематических параметров заместителя. В первую очередь это касается колебаний, отнесенных по форме к типу γ, βCX, полосы которых характеризуются сравнительно малой интенсивностью в спектрах ИК и КР. Имеет место факт слабой интенсивности для большинства полос, отнесенных к неплоским деформационным колебаниям шестичленного циклического фрагмента моногалоидозамещенных бензохинона.

Предлагаемая интерпретация спектра фундаментальных колебаний моногалоидозамещенных гамма-пирона, представленная в табл. 4, является предсказательной. Располагаем только экспериментальными данными [9] для базового соединения – гамма-пирона (ГП).

Таблица 4

Интерпретация спектра фундаментальных колебаний галоидозамещенных гамма-пирона (ГП)

Форма колебаний	ГП	ГП-d2	2F-ГП			2Cl-ГП			ГП-d3	3F-ГП			3Cl-ГП
Форма колебаний	νэкс	νвыч	νвыч	ИК	КР	νвыч	ИК	КР	νвыч	νвыч	ИК	КР	νвыч	ИК	КР
Qc = o	1700	1695	1701	499	47	1699	454	52	1691	1702	388	54	1706	338	38
Q, β, γ	1637	1617	1664	141	15	1628	85	20	1624	1645	18	25	1628	35	41
Q, β	1593	1561	1591	20	6	1566	46	9	1573	1584	21	10	1565	0	6
β	1417	1386	1374	11	2	1375	20	2	1385	1388	15	0	1377	13	2
β, Q, γ	1398	1355	1357	320	0	1321	297	0	1369	1361	13	4	1335	25	5
β	1216	1236	1230	1	3	1223	27	6	1304	1292	48	2	1298	101	2
qCX	3089	2318	1205	114	5	1047	136	4	2297	1227	164	5	1035	120	5
β	1197	1198	1177	18	0	1189	1	1	1185	1161	99	4	1190	8	6
β, Q, γ	1029	1067	1026	6	8	1013	10	11	1099	1094	6	2	1081	4	2
γ, Q	1004	987	928	73	4	918	74	7	1002	968	34	12	951	82	8
γ, Q	922	951	912	1	3	856	6	2	917	862	38	4	836	9	12
γ, Q	790	841	743	7	16	699	12	11	760	722	8	11	666	11	6
γ	474	491	532	6	4	501	2	4	488	577	4	7	538	9	7
γ, βC = O	638	623	513	3	3	472	9	0	627	538	7	3	517	5	3
γ, βC = O	453	444	481	6	1	405	8	8	436	440	1	1	373	0	3
βCX	1319	880	360	8	1	258	2	3	851	290	1	1	225	1	2
ρ	969	947	944	0	0	951	0	1	947	946	0	0	948	0	0
ρ, χ	922	900	847	76	1	867	51	1	911	861	40	1	881	20	1
ρ	857	775	811	3	2	818	17	2	846	831	35	2	835	49	1
ρC = O, χ	790	734	707	1	3	709	1	3	765	737	0	3	740	0	3
ρCX, χ	724	709	648	5	2	586	0	2	628	503	10	1	481	7	3
χ	430	423	404	6	1	403	7	1	429	401	3	1	401	5	0
χ	–	364	202	0	1	160	2	0	388	296	1	1	253	0	0
χ	–	155	155	6	0	151	5	0	152	132	3	1	119	3	1

Таблица 5

Интерпретация спектра фундаментальных колебаний галоидозамещенных тиопирона (ТП)

Форма колебаний	ТП d2	2F-ТП			2Cl-ТП			ТП-d3	3F-ТП			3Cl-ТП
Форма колебаний	νвыч	νвыч	ИК	КР	νвыч	ИК	КР	νвыч	νвыч	ИК	КР	νвыч	ИК	КР
QC = O, γ	1687	1685	425	66	1682	412	68	1683	1689	389	73	1691	316	52
Q, β, γ	1590	1626	116	18	1595	64	24	1592	1608	21	32	1586	21	42
Q, β	1548	1573	5	3	1554	36	3	1548	1564	17	4	1546	5	8
β, Q	1350	1353	31	1	1354	41	1	1349	1370	16	0	1353	10	0
Q, β, γ	1295	1287	60	1	1271	50	3	1333	1337	28	4	1316	15	6
β, Q	1233	1213	15	1	1230	2	2	1215	1199	10	12	1207	10	10
β, Q	1148	1149	30	12	1146	35	12	1127	1110	55	1	1124	12	3
qCX	2345	1138	146	1	928	72	4	2352	1164	119	3	966	63	2
γ, Q	949	892	2	3	839	36	0	973	885	27	0	828	44	1
γ, Qcs	738	757	3	3	755	1	4	742	786	8	13	764	22	19
Qcs, γ	674	703	20	1	698	23	3	705	738	6	2	730	20	2
γ, Q	665	640	16	16	609	11	12	670	637	22	9	593	10	6
γ, βC = O	552	478	2	8	449	12	3	553	538	8	4	517	14	2
γ, βC = O	425	456	6	1	429	0	9	420	440	2	8	418	4	10
γ	406	390	9	6	343	7	7	407	390	3	4	337	1	5
βCX	848	324	7	0	230	3	2	858	306	1	0	236	1	2
ρ	965	956	0	0	958	0	0	965	954	0	0	958	0	0
ρ, χ	920	857	58	1	879	38	0	892	834	82	0	848	64	0
ρC = O, ρ	812	788	12	3	787	21	2	828	803	2	3	807	9	1
ρ, χ	719	644	19	2	637	16	3	697	679	11	3	677	9	3
ρCX, χ	592	513	1	2	482	5	1	546	426	0	0	406	2	1
χ	365	358	0	0	358	0	0	363	355	0	1	361	1	0
χ	332	191	1	1	159	1	1	353	247	1	1	209	0	0
χ	112	109	4	1	105	4	1	111	101	3	1	91	3	1

Согласно принятому в классическом подходе физическому предположению о сохранении значений параметров адиабатического потенциала при изотопозамещении [2], в табл. 3 предложена интерпретация спектра фундаментальных колебаний для 2-d и 3-d монодейтрозамещенных ГП. Влияние массы дейтерия определяет корреляцию частот колебаний по отношению к ГП, характер которой, предложенный в монографии [2], можно считать обоснованием достоверности отнесения для 2-d и 3-d монодейтрозамещенных ГП.

Обоснованием достоверности предлагаемого отнесения спектра фундаментальных колебаний для позиционных таутомеров (2-Х и 3-Х, X = F,Cl) моногалоидозамещенных ГП может служить характер корреляции частот колебаний по отношению к соответствующим позиционным таутомерам дейтерозамещенных ГП. Характеристичность по частоте имеет место для диапазона выше 1000 см–1, кинематические параметры заместителей определяют смещение полос в диапазоне ниже 1000 см–1. Проявляется и такая закономерность, низкая интенсивность полос, отнесенных к неплоским колебаниям моногалоидозамещенных ГП.

Для тиопирона (ТП) и таутомеров моногалоидозамещенных (ГП) не располагаем экспериментальными данными. Достоверность предсказательной интерпретации спектров, предложенной в табл. 5, может быть обоснована теми же аргументами, что выше выдвинуты для моногалоидозамещенных бензола, бензохинона, гамма-пирона.

Заключение

Сопоставление результатов теоретической интерпретации спектра фундаментальных колебаний рассмотренных моногалоидозамещенных шестичленных циклических соединений с имеющимися экспериментальными данными по спектрам ИК и КР дает основание для следующих выводов.

Метод функционала плотности DFT/b3LYP позволяет осуществлять доверительные предсказательные расчеты колебательных состояний монозамещенных циклических соединений при замещении атома углерода карбонового цикла на атомы кислорода и серы. Такой вывод в периодической литературе был сделан для ряда азациклических шестичленных соединений.

Монозамещения оказывают локальное влияние на силовое поле шестичленного цикла соединений, что проявляется в свойствах характеристичности по частоте фундаментальных колебаний в диапазоне выше 1000 см–1, а также для ряда неплоских деформационных колебаний рассмотренных молекулярных объектов. Кинематические свойства заместителей определяют смещение полос в диапазоне ниже 1000 см–1, отнесенных к плоским деформационным колебаниям валентных углов шестичленного цикла. Интенсивность указанных колебаний в спектрах ИК и КР незначительна. В этот же диапазон попадают и полосы неплоских деформационных колебаний связей СН, С = О, СХ. Большинство из них обладает низкой интенсивностью. Особенно это касается спектров КР.

Полученные результаты могут иметь и практическое значение для обоснования предсказательных расчетов монозамещенных шестичленных циклических соединений, полосы фрагменты-заместители которых проявляются в диапазоне 1600–1200 см–1, что проявляется в факте делокализации по форме для фундаментальных колебаний. В галоидозамещенных шестичленных циклических соединениях такого факта не наблюдается, а в амино-, нитро-, гидрокси-, карбокси-, альдегидо- и более сложных заместителей вызывает трудности в задаче построения структурно-динамических моделей и выделения признаков спектроскопической идентификации возможных позиционных таутомеров и их конформеров.

Рецензенты:

Булатов М.Ф., д.ф.-м.н., профессор, генеральный директор «Гиредмет», г. Москва;

Русаков В.С., д.ф.-м.н., профессор кафедры общей физики, МГУ, г. Москва.

Scientific journal
Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

STRUCTURAL DYNAMIC MODELS OF MONOGALOIDYS SUBSTITUTED SIX-MEMBERED CYCLIC COMPOUNDS IN THE CONDENSED STATE

Fundamental research
Scientific journal | ISSN 1812-7339 | Certificate - PI №77-15598