В условиях стабилизации экономической ситуации в стране актуальной является задача определения разновременных параметров кредитования при становления долгосрочного равновесия на рынке кредитования. Данную задачу возможно решить путем построения динамической модели расчета ставки и величины кредита в долгосрочной перспективе.
При решении поставленной задачи использовали кардиналистскую концепцию, моделирующую поведение потребителя на рынке кредитования. Будем считать, что все факторы, влияющие на объем спроса на кредит, постоянны, кроме процентной ставки. Обозначим через qs(р) – функцию предложения займа кредитной организации, qd(р) – функцию спроса на кредит потенциальным клиентом, p – плату за пользование кредитом (стоимость одного рубля займа), причем вблизи точки равновесия можем считать функции линейными [5]. Прямая функции спроса заемщика имеет отрицательный наклон, который отображает закон спроса (первый закон Госсена) и задается уравнением
qd (p) = a – b∙p (a, b > 0).
Функция предложения имеет положительный наклон, поэтому задается уравнением
qs (p) = m + n∙p (m, n > 0).
Будем считать, что значения коэффициентов a, b, m и n известны, а значит, функции спроса и предложения заданы. Тогда условие равновесия, т.е. когда кредитные организации и клиенты имеют максимальный суммарный выигрыш, определяется двойным равенством:
qs (р*) = qd (р*) = q*
или равносильной системой равенств:
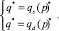(1)
Решением уравнения и системы является плата p*, которую готовы заплатить клиенты и предложить банки за кредит величины
q* = qs(р*) = qd (р*).
Для анализа равновесного состояния на рынке кредитования во времени примем во внимание, что при планировании совершения сделки (непосредственно выдача заемных денежных средств кредитору) клиент и кредитная организация могут оказаться в неодинаковом положении. Клиент, планируя в периоде t получить займ, знает цену займа в этом периоде, а кредитная организация в то же время не имеет представления, какую цену займа к моменту выдачи кредита она способна будет предоставить.
Процесс становления равновесия на рынке кредитования является непрерывным, а потому описывается непрерывной функцией от времени p(t). Так как qs(p) и qd(p) – функции, зависящие от цены рубля займа, то задача поиска долгосрочного равновесия сводится к исследованию зависимостей p(t), qs(p), qd(p) и поиску оптимальной точки p*. На практике ставка кредитования не меняется непрерывно в течение времени. Изменения происходят в определенные дискретные моменты. Поэтому преобразование совокупности входных данных системы (бухгалтерской отчетности, ключевой ставки, уровня риска неплатежеспособности, данных кредитной истории и др.) можно рассматривать как дискретную систему, а функцию p(t) – как дискретную функцию, определенную в моменты времени ti. Входные данные системы являются входными дискретными сигналами.
Процесс дискретизации представляет собой квантование по времени с постоянным периодом
∆t = ti – ti−1,
где ti – некоторый момент времени, а ti−1 – предшествующий ему момент. Если интерполяция полученной дискретной функции p(ti) совпадает с исходной непрерывной функцией p(t), говорят, что дискретизация прошла без потери информации, т.е. исходная функция p(t) совпадает с восстановленной в результате интерполяции. Свойство дискретных систем, позволяющее сохранять однозначность интерполяции в диапазоне 2∙∆t∙Ω ∈ (0, 1], называется стробоскопическим эффектом. Данное свойство является следствием из теоремы Котельникова – Шеннона [4], согласно следствиям из которой
,
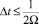где 2Ω – частота дискретизации, а Ω – частота Найквеста, т.е. минимальная частота, с которой нужно посылать импульсы, чтобы не было потери информации. Если 2∙∆t∙Ω > 1, то исходная функция не может быть востановлена. Возникающий эффект называется эффектом появления ложных частот (aliasing). Частота дискретизации определяется максимальной частотой спектра входного сигнала.
В нашем случае необходимо учесть частоту изменения входных параметров, которые используются при расчете значения ставки по кредиту. На ее величину влияют величина риска кредитования, перерасчет которой происходит ежедневно в конце рабочего дня [1]; ключевая ставка или ставка межбанковского кредитования, максимальная частота изменения которых составляет 1 раз в день в первой половине [2]; доход кредитной организации, который планируется ежемесячно.
Таким образом, максимальная частота входных данных составляет 2 раза в день, т.е. частота Найквеста Ω = 0,5. Исходя из этого, согласно теореме Котельникова – Шеннона, максимальный период дискретизации, обеспечивающий преобразование (интерполяцию) дискретной функции в непрерывную без потери информации, равен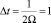 
, т.е. одному дню. Полученные результаты совпадают с практикой, используемой кредитными организациями: изменение ставки по кредиту не производится финансовыми учреждениями чаще, чем 1 раз в день.
Процесс становления долгосрочного равновесия на рынке кредитования может быть отражен динамической паутинообразной дискретной моделью [5], которая позволяет определить процентную ставку по кредиту в момент времени ti на основе данных, полученных в предыдущий момент времени ti–1. Это означает, что предложение по величине цены займа в момент времени ti зависит от цены предшествующего периода ti–1:
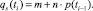
А спрос на заемные денежные средства в момент времени ti зависит от цены заемных денежных средств этого же момента ti:
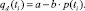
Тогда условие равновесия (1) в момент времени ti можно записать в виде
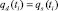
или
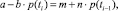
следовательно,
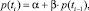(2)
где 
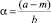и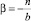 
.
Предположим, что цена займа и объемы спроса и предложения не являются постоянными величинами, т.е. происходит процесс становления долгосрочного равновесия. Исследуем условия, при которых достигается долгосрочное равновесие. Пусть начальный момент времени t0 = 0, тогда при ∆t = 1, значение которого было расчитано выше, t1 = 1, t2 = 2, t3 = 3, и так далее. Тогда
ti = i∙∆t = i
и
ti–1 = (i − 1)∙∆t = i∙∆t − ∆t = ti −1 = i − 1.
Уравнение (2) можно переписать в виде
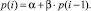(3)
Уравнение вида (3) является линейным неоднородным разностным уравнением. Если дополнительно известна ставка кредитования в начальный момент времени t0, то уравнение (3) совместно с граничным условием p(0) = p0 образуют краевую задачу вида
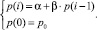(4)
Решение разностного уравнения краевой задачи можно получить одним из двух способов [3]: подстановкой или в виде суммы общего решения однородного разностного уравнения и частного решения неоднородного. Рассмотрим первый способ.
При нахождении решения разностного уравнения путем подстановки из равенства (3) получаем
……....................................................................……………………………….
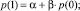
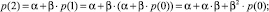
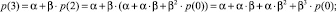
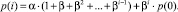(5)
Выражение
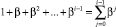
есть частичная сумма ряда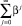 
. Заметим, что
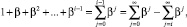
но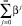 
является рядом геометрической прогрессии со знаменателем q = β, следовательно, он сходится при всех |β| < 1, т.е. при –1 < β < 1 и его сумма равна
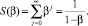
Очевидно, что
тогда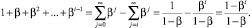 
Подставив полученное значение частичной суммы ряда в (5), получим
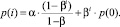
После группировки слагаемых данное уравнение примет вид
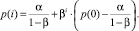
С учетом граничного условия решение можно переписать в виде
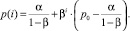(6)
Интервал сходимости ряда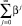 
задается условием |β| < 1, поэтому pt примет конечное значение при 
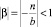, т.е. при b < n. Так как b и n определяют тангенсы углов наклона линий спроса и предложения соответственно, то долгосрочное равновесие в паутинообразной модели является устойчивым только в том случае, когда прямая спроса имеет меньший наклон к оси абсцисс, чем прямая предложения.
Рассмотрим поведение решения p(i) при ti → ∞, т.е. равновесное значение цены займа, которое мы получим в случае, если в системе кредитования не будет происходить никаких внешних или внутренних изменений, влияющих на формирование функции спроса и предложения. Процесс перехода от одного равновесного состояния к другому в течение времени отражается значениями дискретной функции p(ti) = p(i). При ti → ∞ величина p(ti) примет конечное значение, если βt → 0, т.е. когда |β| < 1 или b > n при b > 0 и n > 0. Величины b и n определяют наклоны функций спроса и предложения, поэтому неравенство b > n означает, что прямая предложения имеет больший наклон к оси абсцисс, чем прямая спроса. Рассмотрим графическое изображение. Используем декартову систему координат, в которой ось абсцисс – значение величины кредита q, а ось ординат – величина стоимости одного рубля заемных денежных средств p. Функции спроса и предложения в такой системе координат вблизи точки равновесия имеют линейный вид. На рис. 1 изображен случай существования долгосрочного равновесия.
В случае когда |β| > 1, т.е. когда |b| < n, происходит процесс нарушения равновесия в «паутинообразной» модели. Рис. 2 отражает такой случай.
Предположим, точка долгосрочного равновесия существует, т.е. |β| < 1. Если рассмотреть время как непрерывную переменную, то при t → ∞ и |β| < 1 возможно найти точку долгосрочного равновесия по формуле
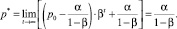
Введем обратную замену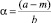 
и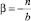 
, получим:
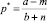и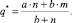 
Можно рассчитать, через какой период времени долгосрочное равновесие будет достигнуто. Для этого необходимо решить уравнение p(ti) – p(ti−1) = 0 относительно ti. Данное уравнение может не иметь решений в области целых чисел, поэтому можно искать значение ti, при котором величина цены на займ не отличается от «следующей» цены на займ на величину ε, равную минимальной цене деления единицы измерения p, т.е. |p(ti) – p(ti−1)| < ε. Единицей измерения цены кредита является рубль, а минимальная цена деления рубля – 1 копейка, поэтому ε = 0,01. Тогда задача сводится к нахождению такого ti, при котором |p(ti) – p(ti−1)| < 0,01. Решим неравенство:
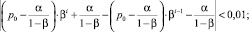
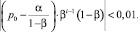(7)
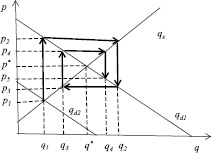
Рис. 1. Становление долгосрочного равновесия «паутинообразной» модели
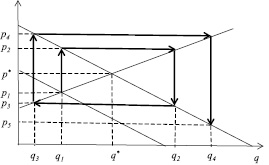
Рис. 2. Нарушение равновесия в «паутинообразной» модели
Прямые спроса и предложения имеют разный наклон,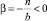 
и |β| < 1, поэтому −1 < β < 0. В то же время p0 > 1 и 
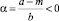, т.к. a > m и b > 0, иначе прямые спроса и предложения не пересекались и равновесной точки не существовало. Поэтому неравенство (7) можно записать в виде
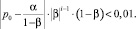
Возьмем логарифм по основанию от обеих частей, поменяв знак неравенства на противоположный, т.к. |β| < 1. Неравенство для периода, необходимого для установления долгосрочного равновесия на рынке кредитования, примет вид
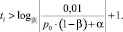
Количество дней, необходимое для установления долгосрочного равновесия, – целое число, поэтому при расчетах использовали функцию int(), которая возвращает ближайшее меньшее целое значение аргумента. Необходимо учитывать, что период становления долгосрочного равновесия будет соответствовать ближайшему большему целому числу. Поэтому неравенство можно переписать в виде равенства:
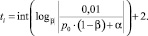
С момента времени ti установившееся долгосрочное равновесие на рынке кредитования не будет изменяться в условиях сохраняющихся внутренних и внешних параметров системы.
Таким образом, зная параметры функций спроса и предложения в изменившихся внешних или внутренних условиях и исходную равновесную ставку по кредиту, можно смоделировать процесс становления долгосрочного равновесия на рынке кредитования, рассчитать значения равновесной точки M (p*, q*) и определить период ti, когда долгосрочное равновесие будет установлено.
Рецензенты:
Лебедев К.А., д.ф.-м.н., профессор кафедры вычислительной математики и информатики, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар;
Уртенов М.А.Х., д.ф.-м.н., профессор, заведующий кафедрой прикладной математики, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар.