В радиотехнике находят широкое применение различные приборы на основе ферритовых элементов, которые необходимо крепить к металлическому корпусу. В большинстве случаев для такого крепления используются клеевые соединения. Однако при возрастании мощности ферритовых приборов и связанного с этим возрастания температурных интервалов работы ферритовых элементов используются паяные и сварные соединения. При этом находят применение так называемые ферритометаллические узлы (ФМУ), которые обеспечивают крепление ферритовых элементов на металлическом корпусе прибора. Сварные соединения целесообразно выполнять диффузионной сваркой (ДС). Процесс ДС предполагает существенные термомеханические воздействия на ферритовые элементы (температуры от 900 до 1000 °С, давления сжатия от 0,1∙107 до 1,5∙107 Па). В этой связи необходимы оценки высокотемпературной прочности ферритовых материалов, без которых невозможно проектирование технологического процесса ДС. В каждом конкретном случае оценка высокотемпературной прочности ферритовых материалов конкретных промышленных марок требует выполнения дополнительных экспериментов.
По характеру механических свойств ферриты относятся к хрупким материалам. При этом известны некоторые методики оценки данных свойств [1, 6], которые показывают, что для ферритов наиболее опасными являются деформации растяжения, изгиба и кручения, предел прочности при которых приблизительно в 10–20 раз ниже, чем при сжатии. В общем случае механическая прочность ферритовых элементов зависит от состояния поверхности изделий, их объема, длительности и скорости прикладываемой нагрузки, микроструктуры, распределения по объему напряжений и дефектов, окружающей среды и температуры.
Техническая прочность ферритов обычно характеризуется значениями прочности, полученными при испытании на контрольных образцах. Однако для ферритов наблюдается большая зависимость прочности от распределения дефектов по объему, что требует учета «размерного фактора», влияние которого заключается в изменении величины прочности с увеличением или уменьшением площади поперечного сечения и объема образца. Указанную особенность объясняет статистическая теория прочности хрупких материалов, связывающая значение прочности с наличием статистически распределенных в изделии дефектов. В изделиях большего объема возрастает вероятность существования дефектов и их сосредоточения в нагруженном сечении, что приводит к уменьшению прочности изделий по сравнению с изделиями меньшего объема (рис. 1).
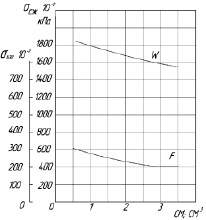
Рис. 1. Влияние объема W и площади поперечного сечения F образца на свойства феррита 50ВЧ2 при различных видах деформации
Из представленной зависимости прочностных характеристик феррита 50ВЧ2 видно, что прочность при всех видах испытаний снижается с увеличением объема и площади поперечного сечения образцов [1].
Для существующих технологий изготовления ферритов характерно наличие в изделиях неоднородностей, дефектов структуры и внутренних напряжений, неупорядоченно распределенных по объему образца. Поэтому при испытании ферритов на прочность наблюдается большая дисперсия величины прочности. Даже в пределах одной партии образцов с одинаковыми значениями площади поперечного сечения и объема дисперсия в отдельных случаях достигает средней величины, находящейся в диапазоне 25–30 %.
Для статистического анализа прочности хрупких материалов и оценки вероятности их разрушения предложено использовать модель Вейбулла (W. Weibull) [2, 4]. Эта модель, основанная на концепции «наиболее слабого звена», рассматривает структуру материала как цепь, прочность которой определяется ее наименее прочным звеном. Вероятность разрушения тела Р задается выражением
P = 1 – exp(–R), (1)
где R – риск разрушения, определяемый для объема V как
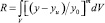для y > yu; (2)
R = 0 для y < yu,
где y – нагрузка, приложенная к элементу dV; yu – предел прочности, т.е. минимальное напряжение, которое может вызвать разрушение; y0 – нормировочный параметр, имеющий размерность «напряжение×объем1/т», и m – модуль Вейбулла, также называемый параметром формы распределения.
Модуль Вейбулла характеризует распределение прочности по величине yu. Когда этот модуль возрастает, кривая распределения прочности по величине сужается. В настоящее время отсутствуют данные по значениям m для ферритовых материалов. В работах по оценке зависимости прочности от размеров образцов стекол [5] значения модуля m изменяются от 4 до 15. Предел прочности yu обычно принимается равным нулю для того, чтобы при нахождении R по уравнению (2) после интегрирования получить функцию только двух параметров, которую легко трансформировать в линейный вид без потери основных результатов анализа. Приравнивание yu к нулю дает заниженные прочностные характеристики материала (переоценка вероятности разрушения), но без какого-либо существенного изменения в самом характере распределения вероятности разрушения.
В этом случае выражение для R может быть записано в простой форме:
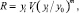(3)
где yi – коэффициент, зависящий от условий нагружения тела.
Основное допущение, которое принимается в рассматриваемом случае при использовании модели Вейбулла, состоит в том, что материал является гомогенной средой с одним типом дефектов, присутствующих в большом количестве и беспорядочно распределенных по материалу.
Тогда можем предположить равенство величин R для разрушения образцов ферритовых элементов разных объемов:
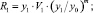
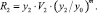
Для R1 = R2 будем иметь
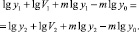
Предполагая равенство коэффициентов y1 и y2, зависящих от условий нагружения в технологическом процессе ДС и объема образцов феррита, получим
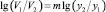
или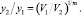 
(4)
Это соотношение показывает, что образец с эффективным объемом V2 характеризуется такой же вероятностью разрушения, как и образец с объемом V1, если напряжения изменяются от y1 до y2.
Соотношение (4) может иметь существенное значение для практики. При серийном производстве одинаковых по форме, но имеющих различные геометрические размеры ФМУ возможно прогнозирование их прочности без выполнения экспериментальных испытаний.
Для определения значений модуля Вейбулла для ферритовых деталей и ФМУ, выполненных диффузионной сваркой, в качестве исходных данных использовалась зависимость прочности на сжатие иттриевых феррогранатов при температурах 900 и 1000 °С в вакууме порядка 1,33∙10–2...6,66∙10–3 Па [3] (рис. 2).
На данном рисунке приведена зависимость σсж от размеров ферритовых деталей в условиях процесса диффузионной сварки.
Используя значения прочности на сжатие σсж для ферритов с объемом 0,3; 0,5; 0,75 и 1,0 см3, а также выражение (4), определялось значение модуля Вейбулла (табл. 1).
Принимая значение модуля Вейбулла для σсж равным 1,8, можно экстраполировать графическую зависимость до объема образцов феррита 2,5 см3.
Для построения зависимости прочности на сдвиг τсдв от размеров образцов ФМУ, выполненных ДС, использовались значения, приведенные на рис. 2, а также экспериментальные данные для размеров ФМУ, составляющих 1,0 и 1,5 см3 (табл. 2).
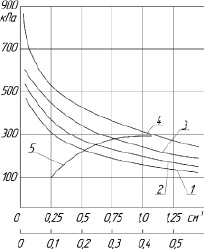
Рис. 2. Зависимость прочности на сжатие σсж ферритогранатов от объема (1–4) и толщины изделий (5) при Т = 900, 1000 °С: 1, 5 – 30СЧ6 (1000 °С); 2 – 30СЧ6 (900 °С); 3 – 40СЧ4 (1000 °С); 4 – 40СЧ4 (900 °С)
Таблица 1
Зависимость σсж от объема образцов феррита 2,5 см3
|
σсж |
||||
|
m |
V1, см3 |
V2, см3 |
y1, кПа |
y2, кПа |
|
1,85 |
0,3 |
0,5 |
220 |
290 |
|
1,82 |
0,5 |
0,75 |
176 |
220 |
|
1,8 |
0,75 |
1,0 |
150 |
176 |
|
1,82 |
1,0 |
1,25 |
132 |
150 |
Таблица 2
Зависимость τсдв от размеров образцов ФМУ
|
τсдв |
||||
|
V, см3 |
y1, кПа |
y2, кПа |
y3, кПа |
yср, кПа |
|
1,0 |
452 |
438 |
406 |
432 |
|
1,5 |
397 |
382 |
361 |
380 |
По выражению (4) определялось значение модуля Вейбулла (табл. 3).
Таблица 3
Значения модуля Вейбулла
|
τсдв |
||||
|
m |
V1, см3 |
V2, см3 |
y1, кПа |
y2, кПа |
|
2,95 |
0,3 |
1,0 |
432 |
650 |
|
3,16 |
1,0 |
1,5 |
380 |
432 |
Принимая значение модуля Вейбулла для τсдв равным 3,0, рассчитывались недостающие значения τсдв для объема ФМУ – 0,5; 2,0; 2,5 см3 и строилась графическая зависимость τсдв для объемов от 0, до 2,5 см3 (рис. 3).
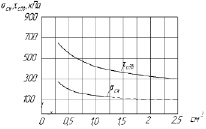
Рис. 3. Зависимость σсж и τсдв от размеров ферритовых образцов
Полученные зависимости использовались для расчетов прочности τсдв ФМУ при проектировании технологических процессов диффузионной сварки.
Таким образом, в настоящей работе проведена оценка высокотемпературной прочности ферритовых материалов, для которых наиболее опасными являются деформации растяжения, изгиба и кручения, предел прочности при которых приблизительно в 10–20 раз ниже чем при сжатии. Используя статическую теорию прочности хрупких материалов, было установлено, что зависимость прочности ферритов от дефектов требует учета размерного фактора. Была предложена зависимость прочностных характеристик от размерного фактора, из которой видно, что прочность ферритов при всех видах испытаний снижается с увеличением объема и площади поперечного сечения образцов. Проведен статистический анализ прочности хрупких материалов и оценка вероятности их разрушения при использовании модели Вейбулла. На основании статистической модели Вейбулла построены зависимости σсж феррита 30СЧ6 при температуре 1000 °С и τсдв для ФМУ на основе диффузионного соединения от объемов ферритовых образцов.
Выводы
1. Предложен метод прогнозирования высокотемпературной прочности деталей из ферритогранатов для процесса ДС на основе модели Вейбулла.
2. Полученные оценки справедливы для ферритовых элементов, имеющих форму пластин объемом от 0,3 до 2,5 см3.
Рецензенты:
Бекренев Н.В., д.т.н., профессор, заведующий кафедрой «Техническая механика и детали машин», ФГБОУ ВПО «Саратовский государственный технический университет имени Гагарина Ю.А.», г. Саратов;
Игнатьев А.А., д.т.н., профессор, заведующий кафедрой «Автоматизация, управление, мехатроника», ФГБОУ ВПО «Саратовский государственный технический университет имени Гагарина Ю.А.», г. Саратов.