Ухудшение социально-экономических условий жизни населения страны, нарастание экологического неблагополучия приводят к изменению качества жизни студенческой молодежи [1, 2]. К сожалению, далеко не всегда образ жизни современного молодого человека можно назвать здоровым. Негативные тенденции в состоянии здоровья студенческой молодежи возникают также за счет воздействия неблагоприятных факторов обучения. Интенсификация учебных программ приводит к значительному увеличению учебной нагрузки, и, соответственно, избыточной напряженности умственной деятельности [4, 5]. Все эти неблагоприятные факторы, в конечном итоге, отрицательно воздействуют на состояние здоровья молодого человека и приводят к функциональным отклонениям и хроническим заболеваниям [10].
В связи с актуальностью вышеизложенного в нашем исследовании большое внимание уделяется комплексной оценке состояния здоровья и образа жизни студенческой молодежи.
В настоящее время нами проводится анализ данных заболеваемости студентов по обращаемости, с временной утратой трудоспособности в случаях и днях, а также госпитализированной заболеваемости. Исследуемый контингент насчитывает более 2 тысяч человек, обучающихся в 4 высших учебных заведениях г. Уфы. Данные по заболеваемости берутся из учетной документации студенческой поликлиники. Выкопировка нозологических форм осуществляется в соответствии с международной классификацией болезней десятого пересмотра. Сведения собираются в порядке текущей регистрации, на основе сплошного учета всех заболеваний.
Для оценки полученных данных нами используются нейросетевые инструментарии [3, 7]. Нейросетевые информационные технологии проявили себя весьма успешно как универсальные средства в задачах аппроксимации, распознавания образов, прогнозирования, ранжирования, способных работать в условиях неопределенности (так называемой триады «НЕ-факторов»: неточности, неполноты, неопределенности в данных). Однако, как показали наши исследования, существуют предельные уровни и объемы зашумленности данных по заболеваемости студентов, когда нейросеть теряет свои прогностические способности и начинает аппроксимировать в большей степени шум, чем восстанавливаемые зависимости. При этих условиях нейросетевая модель теряет устойчивость. Данный вопрос в литературе практически не исследован. Ему посвящается данная статья.
Целями вычислительных экспериментов были:
1. Обнаружение неустойчивости НСМ типа многослойного персептрона при росте шумовой составляющей в данных по анализу заболеваемости студентов высших учебных заведений.
2. Анализ условий возникновения неустойчивости НСМ при оценке результативности данных по заболеваемости.
Идея постановки модельного вычислительного эксперимента была предложена Д.В. Полупановым [6].
Исследуем вопрос о влиянии возмущений на качество обучения НСМ. Вышеописанные характеристики искажения делают невозможным варьирование параметров возмущения по отдельности на реальных данных. Поэтому сконструируем модельный пример, задающий базу данных, т.е. обучающее и тестовое множество НСМ, следующим образом. Введем величины pi∈[p0; pN], где p0 = 1, pN = 7,8, pi = p0 + i(pN – p0)/N и qi∈[q0; qN], где q0 = 4,6, qN = 1, qi = q0 + i(qN – q0)/N,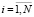 
, N = 200. Сконструируем 10 факторов:
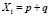; X2 = pq;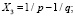 
; 
;
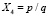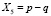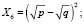
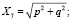(1)
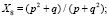
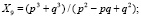(2)
Зададим моделируемую детерминированную зависимость:
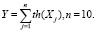(3)
Вычислительный эксперимент проводился на модельных данных для того, чтобы знать неискаженные значения входных факторов (1) – (2) и выходной величины (3). Составим матрицу наблюдений A = {aij}. Здесь aij = xij,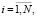 
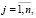ai,n + 1 = yi. В получившейся матрице строки перемешаем случайным образом. Первые 100 строк будут обучающим множеством, другие 100 – тестовым. Тестовое множество обозначим T = {tij}. Здесь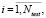 
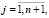Ntest = 100. Детерминированная зависимость (3) аппроксимировалась при помощи нейросети типа многослойный персептрон с двумя скрытыми слоями и активационной функцией гиперболического тангенса [9].
Качество обучения сети на каждой итерации оценивалось по обобщенному критерию J, представляющему собой произведение двух частных критериев:
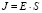; (4)
; 
;
; 
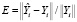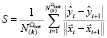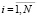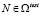, (5)
где yi – точное значение функции Y по (3) в i-ой строке модельных данных;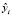 
– рассчитанное обученной и протестированной нейросетью значение моделируемой величины Y.
Величина E в (4), (5) является ошибкой обобщения, рассчитанной на тестовом множестве Ωtest наблюдений, не участвовавших в обучении НСМ, и характеризует точность и прогностические свойства сети. Величина S также вычисляется на тестовом множестве Ωtest. Критерий S характеризует устойчивость НСМ к вариации переменных: чем меньше S, тем меньше разброс значений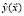 
на новых наблюдениях после обучения нейросети.
Результаты исследования и их обсуждение
Сначала сеть была обучена на незашумленных данных, показатели качества обучения, вычисленные по (4)–(5) следующие: E = 0,0013, S = 0,01078, J = 0,000014. Далее обученной на «эталонных» данных сети предъявлялись зашумленные данные, для того чтобы определить, как будут меняться показатели качества при разном уровне шума. Зашумлению было подвергнуто тестовое множество исходной базы данных, состоящее из 100 вектор-строк. Зашумлению подвергнуты не все столбцы (факторы), а только X1, X3, X5, X7, X9, Y. Столбцы X2, X4, X6, X8, X10 оставались незашумленными. Выбор зашумленных и незашумленных факторов случаен. При этом для факторов X1, X5, X9 и моделируемой величины Y был выбран нормальный закон распределения шумов, а для факторов X3, X7 – равномерный, т.е. использовался смешанный шум. Рассмотрим случайные величины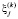 
, h(k), распределенные по нормальному закону:
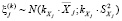, (6)
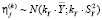, (7)
где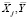 
– средние арифметические вдоль столбцов; 
, 
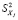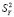– дисперсии величин Xj, Y; 
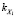, kY – параметры, характеризующие задаваемый уровень шума в столбцах Xj и Y соответственно. Рассмотрим также случайные величины 
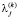и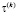 
, равномерно распределенные на интервалах:
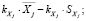
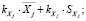
и
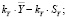
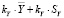. (8)
Сгенерируем по 100 значений случайных величин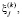 
h(k), 
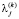и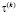 
. Добавив шумовую составляющую к исходным данным, получим возмущенное тестовое множество
,
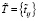где
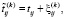
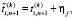
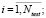
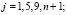(9)
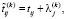
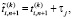
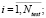
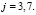(10)
Параметр k, характеризующий интенсивность шума, выбирался произвольным образом для каждого фактора Xj и моделируемой величины Y. Рассмотрим евклидовы нормы исходной и зашумленной матриц, составляющих тестовое множество:
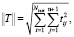
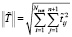. (11)
Величину, характеризующую меру интенсивности возмущения тестового множества, определим как
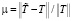. (12)
Рассмотрим зависимость показателей качества обучения сети (4)–(5) от интенсивности возмущения данных m. Для этого будем последовательно увеличивать количество зашумленных строк и предъявлять зашумленные данные нейросети, обученной на «эталонных» данных. Долю зашумленных строк матрицы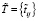 
обозначим w. В табл. 1 и на рисунке отражены результаты тестирования нейросети.
При появлении шума в данных все показатели качества сети резко ухудшаются [8]. Например, уже при w = 0,1 (зашумлено 10 % строк тестового множества) ошибка обобщения составляет 33,9 %, что делает сеть непригодной для ответственных практических расчетов оценки заболеваемости студентов. Следует отметить, что при работе с реальными (не модельными) данными, доля зашумленных данных может быть значительно больше 10 %.
Таблица 1
Показатели качества обучения при разном уровне шума
|
w |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
m |
1,000 |
1,098 |
1,179 |
1,241 |
1,307 |
1,395 |
1,477 |
1,535 |
1,586 |
1,660 |
1,685 |
|
E |
0,00130 |
0,339 |
0,435 |
0,477 |
0,496 |
0,515 |
0,528 |
0,536 |
0,545 |
0,550 |
0,553 |
|
S |
0,01078 |
0,098 |
0,266 |
0,417 |
0,506 |
0,654 |
0,906 |
1,068 |
1,091 |
1,267 |
1,473 |
|
J |
0,000014 |
0,033 |
0,115 |
0,199 |
0,251 |
0,337 |
0,479 |
0,572 |
0,593 |
0,697 |
0,814 |
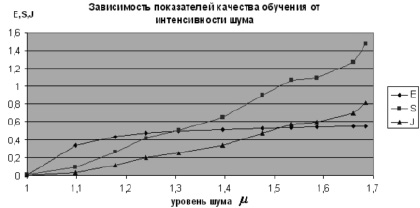
Зависимость E, S, J от интенсивности шума m
При уровне шума m = 1,535 и доле зашумленных строк данных w = 0,7 критерий устойчивости S > 1, нейросетевое отображение становится «растягивающим»: кривые E, S, J начинают расти экспоненциально при увеличении m. Можно сделать вывод, что при некотором критическом уровне зашумленности данных mкр нейросетевая модель становится неустойчивой. При проведении вычислительных экспериментов на реальных данных выяснилось, что сеть становится неустойчивой при гораздо меньшем значении w. Объясняется это более сложной и недетерминированной зависимостью факторов и моделируемой величины. Относительно небольшие возмущения входных данных могут приводить к значительному искажению нейросетевого отклика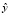 
.
Полученные на модельном примере результаты подтверждают идею о необходимости и полезности регуляризации НСМ, т.е. обеспечивания ее устойчивости. Можно сделать следующий вывод: для построения качественной нейросетевой модели необходима предварительная подготовка (предобработка) данных, направленная на повышение их однородности. Предложенные авторами процедуры удаления противоречивых и аномальных наблюдений позволяют ослабить нежелательные последствия шума и добиться нужных прогностических свойств и точности модели. Интересно, что зависимость ошибки обобщения от интенсивности шума носит экспоненциальный характер.
Для того чтобы подтвердить эффективность предлагаемых процедур удаления противоречивых и аномальных наблюдений, проведем еще один вычислительный эксперимент. Суть его в следующем: к исходной базе данных A = {aij}, состоящей из 200 вектор-строк, добавляется шумовая составляющая согласно правилам (9)–(10), формируется зашумленная база данных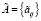 
для обучения нейросети. Пусть w = 0,2, это значит, что 40 из 200 строк базы данных зашумлены. Зашумленные данные были промаркированы, для того чтобы оценить эффективность предлагаемых процедур регуляризации.
К полученной базе данных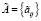 
применим процедуру удаления противоречивых наблюдений и итерационную процедуру удаления аномальных наблюдений. После добавления шума в базе данных 
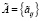появилось 19 противоречивых пар вектор-строк. После их удаления в базе данных осталось 188 строк, 28 из которых содержат шум. Отметим, что в результате выполнения этой процедуры не все зашумленные строки были выявлены и удалены из базы данных. Можно дать следующее объяснение: процедуру удаления противоречивых наблюдений можно отнести к процедурам предрегуляризации модели, т. е. на этом этапе из зашумленной базы данных удаляются самые грубые неоднородности, дальнейшая чистка базы данных происходит на этапе обучения сети. После этого была проведена итерационная процедура обучения сети с удалением на каждой итерации аномальных наблюдений. На каждой k-й итерации фиксировались показатели качества обучения (4)–(5), число аномальных наблюдений А и уровень отбраковки ξ(k) (табл. 2).
Таблица 2
Показатели качества обучения сети на каждой итерации при очистке базы данных от аномальных наблюдений
|
(k) |
1 |
2 |
3 |
4 |
5 |
Обучение без шума |
|
N |
188 |
180 |
172 |
163 |
158 |
200 |
|
A |
8 |
8 |
9 |
5 |
– |
– |
|
ξ(k) |
10 % |
4 % |
3 % |
2 % |
– |
– |
|
E |
0,5280 |
0,0741 |
0,0509 |
0,0325 |
0,0079 |
0,00130 |
|
S |
0,9064 |
0,0913 |
0,0939 |
0,0675 |
0,0978 |
0,01078 |
|
J |
0,4786 |
0,0067 |
0,0047 |
0,0021 |
0,00077 |
0,000014 |
В табл. 2 обозначено (k) – верхний индекс – это номер итерации по удалению аномальных наблюдений из данных; А – число удаленных аномальных точек; ξ(k) – процент удаленных точек.
Как видно из табл. 2, после 4-й итерации в базе данных осталось 158 наблюдений. После обучения и тестирования сети на оставшихся данных, показатели качества обучения достигли желаемых значений, и процесс удаления аномальных наблюдений был остановлен. Из 158 наблюдений оставшихся в базе данных, только 3 строки содержат шум (они были промаркированы и отслеживались). Таким образом, 37 из 40 зашумленных строк были обнаружены и удалены из данных. При этом показатели качества обучения приблизились к значениям, наблюдавшимся при обучении сети на эталонных (незашумленных) данных (для удобства сравнения они приведены в последнем столбце табл. 2).
Выводы
1. Проведенные вычислительные эксперименты подтвердили гипотезу о необходимости предобработки данных в целях повышения однородности, информативности и повышения качества обучения нейросетей в задачах, для которых характерны зашумление или сознательное искажение первичных данных.
2. На модельном примере показана эффективность и состоятельность процедур удаления противоречивых и аномальных наблюдений. Особое значение имеет то, что процесс поиска и удаления аномальных наблюдений проводится итерационно, взаимосвязанно с обучением нейросети при оценке данных по заболеваемости студентов высших учебных заведений.
3. Общая предлагаемая концепция исследований в статье: если имеют место сложные условия моделирования, то есть большая числовая мера интенсивности возмущения m(k), которые устранить нельзя, то нужно парировать эти условия (вырабатывать у НСМ «иммунитет» к указанным возмущениям):
- осуществить предобработку данных в направлении повышения их однородности и информативности; при этом предобработка интерпретируется как предрегуляризация нейросетевой модели, оценивающей показатели заболеваемости студентов;
- осуществить регуляризацию нейросетевой модели здоровьесбережения студентов на основе байесовского подхода.
Вопрос о реализации предложенной концепции является предметом отдельной публикации. Отметим лишь, что она оказалась успешной («зачатки» такой реализации уже видны из табл. 2).
Направления дальнейших исследований:
1. Необходимо детально проработать процедуры предобработки реальных данных опросных анкет, посвященных изучению условий жизни студентов различных высших учебных заведений.
2. Необходимо разработать метод байесовской регуляризации нейросетевых моделей применительно к сложным условиям моделирования (триады «НЕ-факторов»), близким к реальным, где закон распределения плотности вероятности шумов в данных не может быть априори заданным. Применить данный метод для оценки образа жизни студентов с дальнейшим прогнозированием заболеваемости в зависимости от образа и условий жизни.
3. Апробировать разработанные подходы в образовательных организациях.
Рецензенты:
Лобанов С.А., д.м.н., профессор кафедры охраны здоровья и безопасности жизнедеятельности, ФГБОУ ВПО «Башкирский государственный педагогический университет им. М. Акмуллы», г. Уфа;
Горбушина С.Н., д.п.н., профессор кафедры стандартизации и сертификации Уфимского государственного авиационного технического университета, г. Уфа.