При бурении и последующей эксплуатации нефтяных скважин в призабойной зоне образуются органические и неорганические структуры, приводящие к повышению фильтрационного сопротивления и снижению производительности скважин. Для снижения фильтрационного сопротивления и восстановления потенциальной производительности скважин необходимо разрушение этих структур в процессе физико-химической обработки. Экспериментальные и промысловые исследования позволили определить состав отложений в околоскважинной области пласта, однако механизмы возникновения этих отложений и возникновения дополнительного фильтрационного сопротивления в этой зоне изучены недостаточно. В этом случае применяемые методы интенсификации притока скважинной жидкости часто необоснованны, параметры этих методов неоптимизированы и имеют низкую эффективность [1].
При таких обстоятельствах альтернативы тепловым методам воздействия на призабойную зону в настоящее время, по-видимому, нет, поскольку повышение температуры пластового флюида однозначно уменьшает его вязкость и способствует растворению парафинов [2]. Тепловое воздействие на призабойную зону пласта снижает вероятность образования парафинистых и смолистых отложений и способствует увеличению текущей и суммарной добычи нефти, увеличивает межремонтный период эксплуатации скважины, так как уменьшается количество парафина на стенках труб и в выкидных линиях. В большинстве случаев с их помощью удается добиться существенного увеличения притока жидкостей либо повышения приемистости нагнетательных скважин. В других случаях эффект от тепловых воздействий отсутствует. Это объясняется тем, что пока недостаточно ясны механизмы разнообразных явлений, сопровождающих распространение тепла по флюидонасыщенным пористым средам.
Цель исследования. Для решения вопросов применения тепловых методов обработки пласта и оптимизации параметров этих методов необходима разработка и анализ простой математической модели прогрева скважины и пласта и проведения с помощью этой модели оценки эффективности, например, электропрогрева скважины. Такая модель позволит оценить характерные параметры прогрева нефтедобывающих скважин, разработать инженерный модуль по расчёту эффективности электропрогрева нефтяных скважин и использовать эту модель для оценки комбинированных методов воздействия на пласт [3].
Материалы и методы исследования
Рассмотрим плоскорадиальную задачу распространения тепла от нагреваемой скважины в пласт и фильтрационного течения холодного флюида к скважине. В этом случае уравнение теплопереноса имеет вид
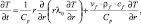(1)
где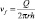 
– скорость фильтрации; ρf, cf – плотность и удельная теплоемкость пластового флюида; λ0 – коэффициент теплопроводности пласта; Cp – объемная теплоемкость пласта; Q – дебит скважины.
Уравнение неразрывности для пластовой жидкости:
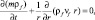(2)
где m – пористость среды.
Закон фильтрации Дарси:
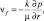(3)
где k – проницаемость породы; μ – вязкость.
Пусть вязкость флюида зависит от температуры:
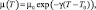
где μ0 – вязкость при пластовой температуре T0; γ – температурный коэффициент вязкости.
Оценки показывают, что время гидродинамической стабилизации намного меньше тепловой [4]. Поэтому для решения тепловой задачи можно выбрать развитый профиль течения под действием постоянного градиента давления. С учётом этого из уравнений (2) и (3) получим эффективность прогрева как отношение дебитов после прогрева Q и до прогрева Q0 [3]:
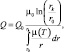(4)
здесь Q0, r0 и rk – первоначальный дебит, радиус и радиус контура питания скважины.
Граничные условия на забое скважины и на радиусе контура питания имеют вид
T(r0, t) = Tc,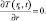 
В безразмерных переменных:
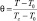– безразмерная температура;
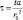– безразмерное время;
(
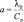– коэффициент температуропроводности пласта);
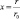– безразмерная координата.
Уравнение (1) запишется следующим образом:
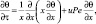(5)
где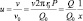 
– безразмерная скорость фильтрации флюида; P – мощность пласта; 
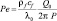– число Пекле, отношение конвективного теплопереноса к кондуктивному.
Если ввести обозначения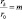 
(m = 2, 3, 4, 5, 6...), то x = 1 – скважина, x = m – контур.
Условие (4) запишется следующим выражением:
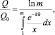(6)
где γ(TC – T0) = k.
Результаты исследования и их обсуждение
Сформулированная задача решалась численно конечно-разностным методом по неявной схеме [5].
При вычислениях приняты следующие параметры среды:
λ0 = 1,28 Вт/(м∙К); Cр = 1378000 Дж/(м3∙К);
ρf = 949 кг/м3; Cf = 1873 Дж/(м3∙К);
μ0 = 1,318 Па∙с; γ = 0,064 К–1; h = 8 м.
На рис. 1 показана зависимость эффективности прогрева (повышение дебита скважины при разных начальных дебитах (до обработки) Q0 = q в зависимости от температурного коэффициента вязкости, при времени прогрева τ = 10. Наибольшую эффективность прогрева могут показать скважины с наименьшим начальным дебитом, поскольку при малых дебитах может формироваться достаточно широкая зона прогрева.
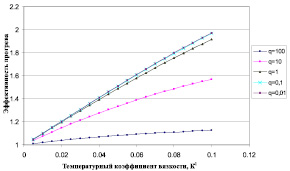
Рис. 1. Зависимость эффективности прогрева от температурного коэффициента вязкости
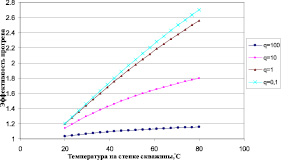
Рис. 2. Зависимость эффективности прогрева от температуры нагревателя
На рис. 2 показана зависимость эффективности прогрева от температуры нагревателя (на стенке скважины) при разных начальных дебитах и постоянной температуре на контуре T0 = 20 °С, при времени прогрева τ = 10.
Зависимости показывают, что влияние температуры подогрева на эффективность тем сильнее, чем меньше начальный дебит скважины.
На риc. 3 приведены профили распределения безразмерной температуры в пласте при разных дебитах, при времени прогрева τ = 10.
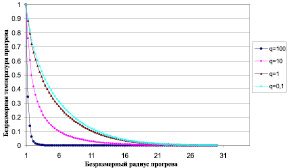
Рис. 3. Распределение температуры в пласте
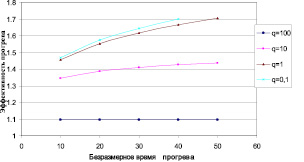
Рис. 4. Зависимость эффективности прогрева от времени нагрева
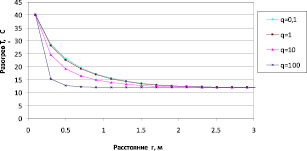
Рис. 5. Профиль температур в пласте при T0 = 12 °С, TС = 40 °С, r0 = 0,15 м
Рис. 4 показывает зависимость эффективности прогрева от времени работы нагревателя для разных дебитов.
Рис. 5 показывает распределение температур в пласте для разных дебитов скважины.
Заключение
Приведённые зависимости имеют очевидное объяснение, подтвержденное опытом применения электропрогрева для интенсификации притока скважинной жидкости – прогрев скважины наиболее эффективен для малодебитных скважин.
Рецензенты:
Миронов В.М., д.ф.-м.н., профессор кафедры «Общая физика и физика нефтегазового производства», Самарский государственный технический университет, г. Самара;
Митлина Л.А., д.ф.-м.н., профессор кафедры «Общая физика и физика нефтегазового производства», Самарский государственный технический университет, г. Самара.