Метод группировки объектов системы на классы позволит определять подобные по своим составляющим объекты, входящие в сложную систему, которые относятся к определяемому классу [6].
Для определения всех объектов, которые подобны по своим характеристикам, заданным в рассматриваемой системе, возможно применение итеративного метода кластерного анализа.
Базовая информация (БИ) представима в виде следующего множества {Pi,j, Ai, Вj}, где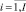 
– индекс объектов, т.е. носителей; 
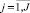– индекс всех характеристик выбранных рассматриваемых объектов; Pi,j – количественное значение j-й характеристики для i-го объекта; Ai – наименование i-го объекта; Вj – наименование j-й характеристики.
Для требуемых значений характеристик лицо, принимающее решение (ЛПР), определяет центр тяжести формируемого класса объектов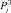 
.
Все элементы Pi,j разделим на группы – принадлежащие и не принадлежащие классу с точностью TI.
Процесс разбиения информации на группы объектов представлен следующим образом:
0. Формирование исходного разбиения осуществляется на основе вспомогательной информации с использованием {ri, di, ai, ki} размерностью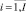 
:
ri – смешанный момент корреляции Карла Пирсона или угловая мера
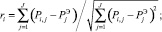(1)
di – евклидово расстояние от заданного центра тяжести до Pi,j
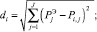(2)
ai – индекс объекта в соответствии с Pi,j;
ki – признак принадлежности i-го объекта к выбранному классу (0 – принадлежит, 1 – не принадлежит, изначально все ki = 1).
1. При первичном разбиении на группы необходимо выполнить следующие два этапа.
1.1. Вначале:
– первоначально i = 1;
– определяется значение s, где s – среднее расстояние между всеми элементами – di
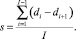(3)
1.2. Рассчитывается расстояние между текущим элементом группы и следующим Δd = di – d(i + 1).
1.3. Проверка условия на принадлежность объекта к выбранному классу осуществляется в процессе выполнения следующих шагов:
Если Δd ≤ s, то k(i + 1) = 0, i = i + 1 и:
– если i ≤ I, то переходим к пункту 1.2;
– если i > I, то осуществляется переход к пункту 1.4.
Если Δd > а, то i = i + 1 и переход к пункту 1.2.
1.4. Далее необходимо объединить классы на основе смешанного момента корреляции Карла Пирсона ri.
1.5. Вначале:
– элементы {ri, ki} распределяются по возрастанию элементов ki и ri соответственно;
– определяем i = 1.
1.6. Определяем пороговое значение α, на основании данного параметра определяется принадлежность i + объекта к рассматриваемому классу [2, 4]:
α = (ri – r(i + 1)).
Если α = 0, то i = i + 1 и α вычисляется заново.
Если α < 0, то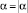 
и i = 1.
Если α > 0, то i = 1.
1.7. Проверка на выполнение условия, признака окончания всех объектов класса.
Если ki = 0, то переход к пункту 1.8.
Если ki = 1, то переход к пункту 1.10.
1.8. Определяется расстояние между текущим и следующим элементами:
Δr = ri – r(i + 1).
1.9. Проверяется принадлежность i + 1 объекта к рассматриваемому классу:
Если Δr > α, то k(i + 1) = 1, i = i + 1, и:
– если выполняется условие i ≤ I, то переходим к пункту 1.7;
– если выполняется условие i > I, то переход к пункту 1.10.
1.10. Второй этап завершен. В результате Pi,j разбиваются на две группы.
2. Вычисляются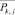 
– центры тяжести полученных групп:
,
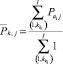К = 2 – индекс полученных групп.
3. Проверяется, находится ли каждый объект в ближайшей группе.
3.1. Первоначально i = l, n = 0.
3.2. Вычисляется квадрат отклонения объекта αi от центра тяжести групп:
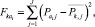(4)
где k = 2 – индекс полученных групп;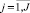 
– индекс характеристики, участвовавшей в формировании результата Pi,jai объекта.
3.3. Если достигается min(Frai) при k = ki, то рассматриваемый объект – ai находится в ближайшей группе и изменение класса не происходит.
Если достигается min(Fkai) при k ≠ ki, тo объект – ai соответственно не находится в ближайшей группе и поэтому ki = k и n = n + 1 [5].
3.4. Увеличивается i = i + 1 и выполняется:
– если i > I, то закончился просмотр всех объектов и переход к пункту 4;
– если i ≤ I, то переход к пункту 3.2.
4. Если: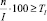 
требуемая точность не достигнута, то осуществляется возврат к пункту 2.
Если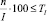 
, то требуемая точность итеративного процесса достигнута. Получено окончательное разбиение Pi,j по классам.
При разбиении объектов управления на классы первоначальными данными являются:
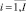– индекс объекта управления;
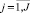– индекс характеристики объекта управления;
Pi,j – количественное значение j-й характеристики i-го;
Ai – наименование i-го объекта;
Вj – наименование j-й характеристики;
ТI – требуемая точность разбиения в процентах;
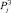– центр тяжести интересующего класса объектов.
Результатом разбиения объектов на группы являются:
ki = 0 – признак, что i-й объект принадлежит к выбранной группе;
ai – индекс объекта в соответствии с Pi,j.
Оценка по выбору управляющих воздействий должна основываться на сравнении получаемых результатов за наблюдаемый промежуток времени с соответствующими значениями параметров из предыдущего периода, основной задачей которых является повышение эффективности сложной системы [3, 7]. Если итоговые значения принятых управляющих воздействий (УВ) не ухудшились, то УВ принимаются как эффективные и соответственно неэффективные в противном случае. Для сравнения результатов УВ обоих периодов необходимо вначале разбить их на близкие по своим значениям характеристик из группы и произвести оценку по групповым параметрам, что позволит уменьшить размерность решаемой задачи [1, 2].
Для выбора из всех объектов, совпадающих по значениям параметров групп объектов, используем методику группирования объектов сложной системы на соответствующие классы. Оценка эффективности выбранных УВ осуществляется следующим образом:
1. Формирование групп объектов по всем параметрам за предыдущий период.
Формируются первоначальные данные, необходимые для использования методики.
Из первичной информации, циркулирующей в сложной системе из множества {Pi,j, Ai, Вj}, выделяем информацию за предыдущий период:
Pi,j – количественное значение j-й характеристики i-го объекта;
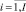– индекс объектов управления, носителей первичной информации;
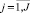– индекс характеристик;
Ai – идентификационные данные i-го объекта;
Вj – наименование j-й характеристики.
ЛПР определяет:
ТI – требуемая точность разбиения в процентах;
KЭ – требуемое количество классов разбиения.
Получим следующие результаты:
К – количество полученных классов;
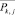– центры тяжести полученных классов;
Ki – номер класса, к которому принадлежит i-й объект;
ai – индекс объекта в соответствии с Pi,j.
2. Формирование групп объектов по значениям их характеристик за рассматриваемый период времени.
Формируются исходные данные, необходимые для использования методики [4, 6].
Из первичных данных выделяется информация за исследуемый период:
Pi,j – количественное значение j-й характеристики i-гo объекта;
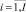– индекс объектов;
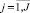– индекс характеристик объектов.
Ai, Bj, TI , KЭ – определены в пункте 1.
В результате работы данного алгоритма будут получены следующие характеристики:
К – количество полученных классов;
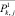– центры тяжести полученных классов;
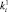– номер класса, к которому принадлежит i-й объект;
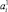– индекс объекта в соответствии с Pi,j;
3. Исследование двух полученных групп классов.
К – количество классов, полученных в пункте 1;
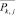– центры тяжести данных классов;
ki – номер класса, к которому принадлежит i-й объект;
ai – индекс объекта Pi,j.
В пункте 2 получены:
К – количество полученных классов;
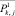– центры тяжести полученных классов;
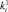– номер класса, к которому принадлежит i-й объект;
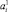– индекс объекта в соответствии с Pi,j.
3.1. Для сравнения полученных классов объектов преобразуются центры тяжести классов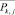 
и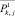 
, чтобы получить оценки сформированных групп классов независимыми от участвующих в анализе характеристик объектов следующим образом:
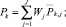(5)
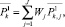(6)
где Wj – коэффициенты значимости j-го параметра исследуемого управляющего объекта, которые определяет ЛПР;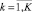 
– индекс полученных классов; 
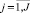– индекс параметров, участвующих в анализе.
Полученные элементы (ai, ki) и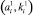 
упорядочиваются в соответствии с ai и 
.
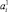3.2. Первоначально S = 0, i = 0, п = 0.
3.3. Есл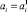и 
и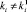 
, тогда 
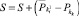и n = n + 1;
3.4. i = i...1.
Если i < 1, то осуществляется переход к пункту 3.3.
Если i ≥ I, то переходим к пункту 3.5.
3.5. Э = S/n∙100.
3.6. Оценка эффективности принятых в исследуемый период УВ:
– если Э ≥ 0, то УВ принимались эффективные;
– иначе – неэффективные.
Рецензенты:
Филатов Г.Ф., д.ф.-м.н., профессор кафедры математики, Военный учебно-научный центр Военно-воздушных сил, «Военно-воздушная академия имени профессора Н.Е. Жуковского и Ю.А. Гагарина», г. Воронеж;
Обуховский В.В., д.ф.-м.н., профессор, заведующий кафедрой высшей математики, Воронежский государственный педагогический университет, г. Воронеж.