Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Высокая волатильность рубля по отношению к иностранной валюте, ряд санкций, выставленных России, повышение уровня инфляции и низкий прирост ВВП в значительной мере повлияли на ситуацию на рынке кредитования [5]. В первую очередь сокращение темпов роста кредитования коснулось предприятий малого и среднего бизнеса. Это связано с высокими рисками сектора в условиях дестабилизации экономики страны. В то же время без развития малого и среднего бизнеса экономический рост страны невозможен. Предпринятые государством и Центральным банком меры по увеличению ключевой ставки, коэффициентов риска и величины резервов на возможные потери по ссудам поставили малый и средний бизнес в еще более затруднительное положение. С одной стороны, кредитные организации опасаются высоких рисков и потому сокращают объемы кредитных портфелей МСБ. С другой стороны, высокая конкуренция на рынке кредитования может привести к переориентации платежеспособного потребительского спроса и, как следствие – к потере клиентов. Таким образом, в условиях ухудшения экономической ситуации в стране задача определения финансового состояния заемщика и расчета его индивидуальных условий кредитования является актуальной для финансовых учреждений.

Современный уровень развития информационных технологий позволяет ставить и решать задачи мониторинга финансового состояния предприятий посредством научных методов многомерного анализа данных, реализованных в статистических пакетах. На основе таких программных модулей пакета STATISTICA, как дискриминантный анализ, деревья классификации, нейронные сети и логит-регрессия, авторами разработана информационная система поддержки принятия решений для оценки финансового состояния предприятий [3] и [4]. Очевидно, что при принятии решений о кредитовании предприятий платежеспособность клиента не может быть определена отдельно от анализа его финансовых возможностей, так как эти два понятия являются взаимодополняющими. Финансовые возможности заемщика должны учитываться при выборе условий (параметров) кредитования, что снизит риски кредитного учреждения. Рассмотрим математическую модель определения таких параметров кредитования предприятий МСБ, как оптимальная процентная ставка, величина и период кредита.

Выбор процентной ставки кредитования должен быть компромиссным (равновесным) между желаниями кредитора и возможностью заемщика. Задачу нахождения оптимального (равновесного) значения процентной ставки по кредиту, выдаваемому кредитной организацией предприятию МСБ, будем рассматривать в условиях совершенной конкуренции на рынке кредитования. Величину ставки и процент определим из условия равновесия, т.е. когда кредитные организации и клиенты имеют максимальный суммарный выигрыш. Считаем, что на рынке кредитования существует некоторое количество кредитных организаций, способных выдавать денежные займы, и некоторое множество клиентов, нуждающихся в этих денежных средствах. Для построения функций спроса и предложения воспользуемся кардиналистской концепцией, моделирующей поведение потребителя на рынке кредитования [1].

Обозначим через q_s(р) – функцию предложения займа кредитной организации, q_d(р) – функцию спроса на кредит потенциальным клиентом, p – плату за пользование кредитом (стоимость одного рубля займа), причем вблизи точки равновесия можем считать функции линейными [1]. Тогда условия равновесия, т.е. когда кредитные организации и клиенты имеют максимальный суммарный выигрыш, определим системой равенств:

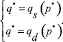(1)

Решение системы – это плата p*, которую готовы заплатить клиенты и предложить банки за кредит величины q* = q_s(р*) = q_d(р*). В декартовой системе координат, в которой ось абсцисс – значение величины кредита q, а ось ординат – величина стоимости p одного рубля заемных денежных средств, функции спроса и предложения вблизи точки равновесия изображаются линейными функциями (рисунок).

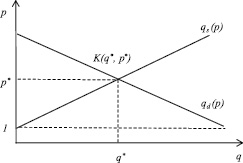
Графическое представление равновесной точки

Область допустимых значений величин p и q ограничена частью плоскости, заданной неравенствами p > 1 и q > 0, так как стоимость рубля заемных денежных средств выше номинальной стоимости рубля и величина кредита не может принимать отрицательных значений. Точка пересечения функций спроса и предложения K(p*, q*) отражает решение системы (1). Если оплата за кредит превышает возможности клиентов, то прямые q_s и q_d не имеют точки пересечения в области допустимых значений q.

Так как финансовые возможности заемщиков различные и изменяются в достаточно широком диапазоне, целесообразно использовать классификацию клиентов по пяти группам (классам) риска неплатежеспособности, которые были описаны в [7]: очень низкий, низкий, средний, высокий и очень высокий уровень риска. Для каждой группы клиентов целесообразно построить свои функции спроса на кредит – q_d и предложения – q_s.

Рассмотрим решение задачи нахождения точки равновесия K(q*, p*) при анутентном способе расчета, когда клиент сначала выплачивает проценты по кредиту, а уже потом – погашает тело кредита, т.е. сумму, взятую в долг у кредитной организации.

Пусть T – период кредитования, который расчитывают в зависимости от запрашиваемой заемщиком суммы и величины его годовой чистой прибыли I, определяемой из данных бухгалтерской отчетности Формы 2 «Отчет о прибылях и убытках». Ежемесячный платеж v может быть расчитан как 40 % от чистой прибыли 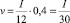рублей или как платеж, равный сумме ежемесячных платежей по погашенным кредитам:

v = Σvi, i = 1, …, n,

где n – количество кредитов, оплачиваемых одновременно без просрочек, а v_i – величина ежемесячного платежа i-го кредита. Пусть клиент запрашивает сумму кредита q₁ рублей. Будем считать, что среднерыночная процентная ставка кредитной организации, соответствующая данной сумме, составляет (p₁ − 1)∙100 %, где p₁ – стоимость одного рубля займа. Тогда с учетом ежемесячного платежа предприятие может погасить запрашиваемую сумму за 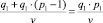месяца.

По усмотрению кредитного аналитика период кредитования T может быть увеличен. При его расчете используют только целое значение, поэтому неравенство, отражающее выбор периода кредитования для заемщика, примет вид

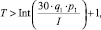
где Int() – функция, которая возвращает ближайшее меньшее целое значение от аргумента.

Задача нахождения точки равновесия K(q*, p*) сводится к построению функций спроса и предложения заемных денежных средств и решению системы (1). Прямая функции спроса заемщика имеет отрицательный наклон, который отражает закон спроса (первый закон Госсена). Будем считать, что все факторы, влияющие на объем спроса на кредит, постоянны, кроме процентной ставки (p − 1)∙100 %, где p – стоимость одного рубля займа, тогда

q_d (p) = a – b·p,

где a > 0, b > 0. У прямой функции предложения в окрестности равновесной точки положительный угол наклона, поэтому функция предложения имеет вид

q_s(p) = m + n·p,

где m > 0, n > 0. Для построения функций спроса и предложения необходимо вычислить значения коэффициентов a, b, m и n. Есть два подхода их вычисления. Первый удобен при портфельном кредитовании, когда у кредитной организации имеется информация о статистических коэффициентах эластичности спроса и предложения для каждой группы клиентов. Второй подход учитывает индивидуальные потребности заемщика, но требует наличия дополнительной информации о клиенте. В данной статье рассмотрен портфельный подход.

Заметим, что эластичность спроса зависит от целей кредитования и уровня риска платежеспособности заемщика. Таким образом, для расчета оптимального срока кредитования и процентной ставки кредитной организации необходима следующая информация: уровень риска неплатежеспособности кредитуемого предприятия МСБ, цель кредитования заемщика, запрашиваемая заемщиком сумма кредита, величина среднерыночной процентной ставки по кредиту, кредитная история клиента, величина годового дохода заемщика, коэффициенты эластичности спроса и предложения по цене для каждой группы клиентов.

Воспользуемся определениями коэффициента эластичности спроса E_d и предложения E_s по цене соответственно

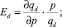
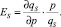
Предположим, что заемщик запрашивает сумму кредита q₁ под средний процент на рынке кредитования (p₁ − 1)∙100 %. В совокупности данные величины образуют точку K₁(q₁, p₁₎ пространства. Тогда в окрестности этой точки получим: 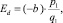откуда 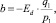следовательно,

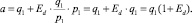
Для построения функции предложения учтем то, что основное влияние на предлагаемую банком ставку по кредиту оказывают ключевая ставка, ставка межбанковского кредитования и ставка по вкладам кредитной организации, а также величина резерва под выданную ссуду. Вся эта информация есть в свободном доступе на сайте Центрального банка Российской Федерации. Какую из ставок использовать для расчета, зависит от политики кредитной организации, которая использует предлагаемую модель.

Согласно [2] под каждую ссуду формируют резерв величиной, определяемой риском кредитования. Систему расчета величины риска кредитования в соответствии с нормативными актами ЦБ РФ можно использовать только после первого платежа по договору займа. Поэтому нами введено понятие категории качества заемщика (категория заемщика), которое применимо к клиенту на этапе подачи заявки на кредитование и является аналогом понятия категории качества ссуды. Категория заемщика вычисляется на основе значений двух критериев: кредитная история заемщика и финансовое состояние предприятия. Кредитная история (КИ) предусматривает пять градаций расчета по долговым обязательствам: очень хорошая (отсутствуют просрочки по долговым обязательствам); хорошая (максимальная просрочка платежа до 30 дней); средняя (максимальная просрочка платежа находится в диапазоне от 31 до 90 дней); плохая (максимальная просрочка платежа находится в диапазоне от 91 до 180 дней); очень плохая (существует просрочка платежа более 180 дней). Финансовое состояние предприятия МСБ определим пятью группами риска неплатежеспособности, о которых было сказано выше. Табл. 1 идентифицирует заемщика по девяти категориям качества.

Значение диапазона кредитного риска R определим из табл. 2.

Во втором столбце таблицы указаны категории ссуды, взятые из [2]. Каждый из диапазонов значений R получен в результате равномерного разбиения значений риска кредитования по категориям ссуды.

Таблица 1

Категории качества заемщика

Таблица 2

Диапазон значений величины риска кредитования по категориям заемщика

Обозначим интервал значений непрерывной величины R Î (α, β), где α – наименьшее возможное значение R для заемщика соответствующей категории, а β – наибольшее. Для расчетов используем безразмерную величину. Например, если заемщик принадлежит к группе «средний уровень риска неплатежеспособности» и в его кредитной истории максимальная просрочка по кредитам составила 10 дней, то клиент относится к 4 категории (см. табл. 1). Тогда значение величины ставки риска определено интервалом 0,01 < R ≤ 0,2.

Чем выше ежемесячный платеж v по кредиту, тем выше риск того, что заемщик не справится со своими долговыми обязательствами. Многие кредитные организации рассматривают величину ежемесячного платежа равную не более 40 % и не менее 10 % от ежемесячного дохода 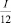. Большие значения платежа рискованны для кредитной организации, а меньшие – невыгодны для заемщика. Поэтому R зависит от отношения 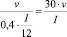, которое принимает значения в интервале от 0,25 до 1. В то же время риск кредитования должен быть соотнесен с долей просрочек от общего числа платежей кредитной истории. Поэтому на значение величины R так же влияет отошение 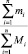, где m_i – количество просрочек по i-му кредиту, M_i – количество платежей по i-му кредиту, n – количество кредитов в кредитной истории заемщика. Таким образом, запишем формулу для расчета значения величины риска кредитования R, зная диапазоны его изменения α и β:

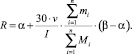(2)

Например, пусть 0,01 < R ≤ 0,2, у клиента была одна просрочка из 25 платежей и платеж по кредиту составляет 37 % от ежемесячной прибыли. Тогда

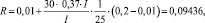
т.е. величина риска кредитования для такого клиента составит примерно 9,44 %.

Пусть кредитная организация может предложить заемщику сумму q₂ = T∙v. Величина q₂ принимает значения, «близкие» к запрашиваемой заемщиком сумме, т.к. |q₁ − q₂| < v:

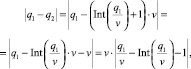
где 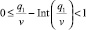, поэтому min(|q₁ – q₂|) = 0, а max(|q₁ – q₂|) = v.

Стоимость одного рубля p₂ заемных денежных средств величины q₂, предлагаемой кредитной организацией, определим равенством

p₂ = 1 + R + k + Income∙(1 + R),

где k – либо ключевая ставка, либо ставка межбанковского кредитования, в зависимости от политики кредитной организации относительно привлечения дополнительных денежных средств; R – величина ставки риска в зависимости от категории качества заемщика, рассчитываемая по формуле (2); Income – доход кредитной организации с каждого рубля денежных средств, использованных для выдачи займа. В качестве дохода рассматриваем балансовую, а не чистую прибыль по кредитным операциям. Согласно [2] по каждой выданной ссуде объемом q формируется резерв величиной (R∙q), обусловленный кредитными рисками, поэтому при расчете дохода кредитной организации прибыль вычисляем с учетом денежных средств, оставленных в резерве, т.е. учитываем величину Income∙(1 + R), а не Income.

В окрестности точки K₂(q₂, p₂) получим 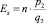, то есть 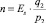. Тогда

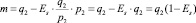
Уравнения функций спроса и предложения принимают вид

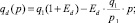
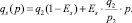
Для нахождения равновесного значения цены кредита и его величины необходимо решить систему уравнений относительно q* и p*:

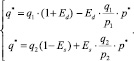
Решением системы являются значения величины кредита q* и стоимости одного рубля заемных денежных средств p*, которые наиболее выгодны для заемщика и кредитора одновременно:

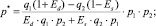(3)

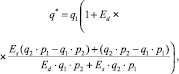(4)

где q₁ – запрашиваемая заемщиком величина денежных средств; p₁ – среднерыночная стоимость одного рубля займа; q₂ – предлагаемая кредитором сумма кредита, стоимость каждого рубля которого составляет p₂.

Таким образом, по величине запрашиваемой клиентом суммы кредитования, зная и учитывая уровень риска неплатежеспособности клиента, его кредитную историю, коэффициенты эластичности спроса и предложения для соответствующей группы риска неплатежеспособности, политику кредитной организации по отношению к источнику дополнительных денежных средств и к запланированному доходу, можно рассчитать оптимальные значения кредита и его процентной ставки.

В соответствии с формулами (3) и (4) был разработан программный модуль, позволяющий произвести расчет величины, срока и ставки кредитования для предприятия МСБ на основе его принадлежности к классу платежеспособности, цели кредитования, данных кредитной истории. Модуль интегрирован в оболочку системы поддержки принятия решения [6]. Система удобна в использовании и не требует от пользователя специальных знаний в области современных методов анализа данных и математического моделирования. Облачная платформа позволяет осуществить мониторинг финансового состояния в режиме реального времени (он-лайн). Для читателей журнала временный бесплатный доступ к системе возможен при использовании следующих параметров входа в систему: логин: FundamRes, пароль: 18127339.

Рецензенты:

Лебедев К.А., д.ф.-м.н., профессор кафедры вычислительной математики и информатики, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар;

Уртенов М.А.Х., д.ф.-м.н., профессор, заведующий кафедрой прикладной математики, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар.