Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Общность производственных ресурсов в сельском хозяйстве вызывает тесную взаимосвязь между всеми его отраслями, которая проявляется также в том, что развитие одной отрасли затрагивает другие. Существует множество вариантов использования каждого ресурса. Кроме того, для сельского хозяйства характерна взаимозаменяемость некоторых видов производимой продукции.

Разработка планов специализации сельскохозяйственного производства имеет своей конечной целью научное обоснование вариантов рационального развития сельскохозяйственного производства на определенную перспективу, определение специализации в объектах, расчет товарного потенциала по всем видам сельскохозяйственной продукции и т.д.

Экономико-математическая задача оптимальной специализации и сочетания отраслей заключается в определении производственной структуры хозяйства. Другими словами, она должна определять оптимальные размеры площадей сельскохозяйственных культур, поголовья отдельных видов и групп скота и т.д. Кроме количественного определения размера площади, проблема правильного сочетания отраслей охватывает сезонность производства сельскохозяйственной продукции.

Модель оптимальной специализации и сочетания отраслей должна отражать оптимальные соотношения между затратами ресурсов и результатами производства, установить баланс между производством и использованием ресурсов для обеспечения рационального использования наличных производственных ресурсов [3, 6].

При трансформации централизованно планируемой экономики в рыночную произошло стихийное разукрупнение сельскохозяйственных предприятий (колхозов, совхозов) и возникновение множества мелкотоварных хозяйств, для которых задача оптимальной специализации перестала играть существенную роль.

В Республике Дагестан сохранилось немало средних и крупных хозяйств в виде различных ГУПов и МУПов (государственных унитарных и муниципальных унитарных предприятий), для которых оптимальная специализация является настоятельно необходимой. Однако их ограниченные финансовые возможности, низкий уровень информатизации, острая нехватка специалистов не позволяют хозяйствам заниматься проблемами оптимизации производства во всех их сферах, в том числе оптимизировать внутриотраслевую специализацию сельскохозяйственного производства.

Целью настоящего исследования является разработка модельного инструментария оптимизации, включающего модели для отдельных предприятий и блочную модель для их совокупности. Модели составлены на примере сельскохозяйственных предприятий Дербентского района Республики Дагестан, специализирующихся на производстве винограда в сочетании с производством и других видов сельскохозяйственной продукции (молока, зерна и мяса и др.).

Одним из первых этапов при разработке математической модели является определение перечня искомых показателей и введение для них символьных обозначений.

Для задачи по оптимальной специализации введены следующие обозначения:

x_j – искомое значение j-й переменной, означающей отрасль хозяйства или вид деятельности;

x_i – искомое значение i-й переменной, означающей расчетный показатель (неизвестные объемы ресурсов, материально-денежных затрат, товарная и валовая продукция и другие суммарные показатели);

c_i – оценка i-й переменной, соответствующая принятому критерию оптимальности;

a_ij – коэффициенты затрат i-го вида ресурсов в расчете на единицу j-й переменной величины;

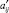– коэффициенты выхода i-го вида ресурсов или продукции в расчете на единицу j-й переменной величины;

b_i – объемы наличных ресурсов за год в целом;

q_ij – коэффициент выхода товарной продукцииi i-го вида в расчете на единицу j-й переменной;

Q_i – минимальный объем продукции i-го вида, производство которого необходимо гарантировать при любом решении задачи;

p_ij – коэффициент, означающий долю i-й сельскохозяйственной культуры в общей посевной площади;

N – множество переменных, означающих все отрасли хозяйства:

N₁ – отрасли растениеводства;

N₂ – отрасли животноводства;

M – группа ограничений:

M₁ – по использованию производственных ресурсов в хозяйстве;

M₂ – по производству и использованию кормов;

M₃ – по производству гарантированного объема продукции;

M₄ – по расчету суммарных показателей производства (валовой и товарной продукции, прибыли и др.);

M₅ – по соотношению посевов сельскохозяйственных культур.

После определения перечня переменных следует определить перечень условий-ограничений. В классической постановке задачи оптимизации внутриотраслевой специализации [3, 6] необходимо найти значения xj, при которых достигает экстремального значения целевая функция 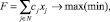при следующих ограничениях:

1) по использованию производственных ресурсов в хозяйстве

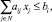(i ∈ M₁);

2) по производству и использованию кормов

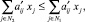(i ∈ M₂);

3) по производству гарантированного объема товарной продукции

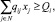(i ∈ M₃);

4) по расчету суммарных показателей производства

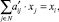(i ∈ M₄);

5) по соблюдению определенных соотношений в посевных площадях сельскохозяйственных культур

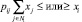(i ∈ M₅);

6) неотрицательности переменных, включенных в задачу

x_i ≥ 0; x_j ≥ 0.

В качестве ограничивающих условий в разработанных моделях приняты площади сельскохозяйственных угодий, поголовье скота, объем продукции, нормы выхода продукции на 1 голову скота и 1 га сельхозугодий, а также величины ряда основных экономических показателей на единицу продукции.

Размерность блочной оптимизационной модели составляет 49×78.

Требуется определить такой план производства {x₁, x₂, …, x₁₂},{x₁₃, x₁₄, …, x₂₄}, {x₂₅, x₂₆, …, x₃₆}, {x₃₇, x₃₈, …, x₄₉}, при котором достигает оптимального значения целевая функция.

Например, для МУП «Чинар» в случае выбора суммарных производственных затрат в качестве критерия оптимальности целевая функция выглядит следующим образом:

F = 617x₃ + 1198x₄ + 10118x₅ + 1418x₆ → min,

где x₃, x₄, x₅, x₆ – искомые объемы зерна, винограда, молока и мяса соответственно.

С помощью общих переменных можно вводить ограничения по соблюдению определенных соотношений в посевных площадях сельскохозяйственных культур хозяйств. В данной задаче это ограничение наложено на площадь виноградников, а именно: площадь виноградников должна составить не менее 60 % от общей посевной площади. Математическая запись этого условия-ограничения выглядит следующим образом:

x₃₇ – 0,6x₄₉ ≤ 0,

где x₄₉ – общая посевная площадь всех трех хозяйств; x₃₇ – общая площадь виноградников.

Кроме того, общие переменные дают возможность задавать гарантированные объемы производства отдельных видов сельскохозяйственной продукции в пределах района и тем самым определить оптимальную специализацию каждого хозяйства.

Фрагмент рабочей матрицы решения задачи приводится в табл. 1.

Таблица 1

Фрагмент расширенной матрицы блочной модели по оптимизации производства сельхозпродукции в хозяйствах Дербентского района РД

Объемы сельскохозяйственной продукции фактически, по оптимальным вариантам, рассчитанным для каждого хозяйства в отдельности (1-й вариант), по оптимальному решению трехблочной задачи (2-й и 3-й варианты) приведены в табл. 2.

Таблица 2

Объем производства сельскохозяйственной продукции в хозяйствах Дербентского района РД фактически и по оптимальным вариантам, рассчитанным с помощью блочной модели

Примечания: 1-й вариант – оптимальные решения, полученные по моделям каждого предприятия; 2-й вариант – по единой блочной модели (критерий оптимальности – суммарные производственные затраты); 3-й вариант – по единой блочной модели (критерий оптимальности – товарная продукция).