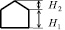Наглядность представления визуальной обстановки населенных объектов и удобство работы с данными являются важными свойствами для информационных систем различного назначения. Компьютерные трехмерные модели городских сцен могут быть использованы для решения следующих задач [2, 3, 4, 9, 12]: проектирования коммуникаций; моделирования чрезвычайных ситуаций (наводнения, пожары), транспортных потоков, процессов микроклимата; планирования схем эвакуации населения и антитеррористических операций; синтеза визуальной обстановки для тренажеров транспортных средств, геоинформационных систем, систем виртуального туризма. Целью работы является разработка алгоритмического и программного обеспечений автоматической трехмерной реконструкции визуальной обстановки городских сцен по спутниковым снимкам.
Для создания трехмерных моделей объектов местности обычно применяются системы трехмерного моделирования, позволяющие создавать геометрию при помощи типовых операций в интерактивном режиме. Однако этот способ достаточно трудоемок. Также в последнее время используется метод на основе лазерного сканирования. Преимуществами такого подхода являются высокая скорость и точность создания трехмерных моделей. Однако в этом случае формируется облако трехмерных точек. Поэтому в автоматическом режиме невозможно выделить характерные объекты из сцены. Например, поверхность рельефа и фасады зданий представляют в такой системе единое целое. Из-за этого трехмерным данным нельзя назначить атрибуты и использовать в качестве физических моделей, имеющих определенные свойства. Кроме того, лазерное сканирование характеризуется большим объемом получаемых данных, что предъявляет высокие требования к вычислительным возможностям систем. Предлагается использовать подход на основе автоматического восстановления трехмерной геометрии по изображениям. В качестве изображений применяются спутниковые снимки высокого разрешения. На снимках могут быть выделены точечные, линейные и площадные признаки, которые в дальнейшем могут быть использованы для распознавания и реконструкции [1, 5, 14, 15]. Создание системы автоматической реконструкции на основе цифровых изображений позволит сократить временные и материальные затраты при синтезе трехмерных моделей.
Для реализации подхода используется заранее предопределенная информация о структуре сцены и условиях получения изображения. Таким образом, процесс синтеза трехмерных данных, представленный в работе, основан на распознавании объектов на видеоизображениях. Для повышения надежности распознавания предлагается использовать структурированную информацию, представленную в виде графов. Для сравнения структур используются спектры графов. Преимуществом структурных методов и алгоритмов является то, что они позволяют анализировать большое множество элементов на основе малого количества простых составляющих и правил формирования графической модели. Также структурные методы позволяют описать те характеристики объекта, которые исключают его отнесение к другому классу, что повышает надежность распознавания.
Модели реконструируемых объектов
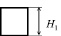
Уровнями детальности (LoD – Level of Detail) называют степень подробности представления трехмерного объекта средствами компьютерной графики [6]. В этом случае создаются несколько вариантов представления одного объекта с различными степенями детализации (рис. 1). Уровни детальности используют для универсального представления, хранения и обмена моделей местности. Ассоциацией OGC (Open Geospatial Consortium) разработан язык CityGML (City Geography Markup Language), который определяет классы и отношения объектов, основываясь на их топологических, семантических и геометрических свойствах [9]. Для процесса трехмерной реконструкции моделей местности предполагается использовать уровень LoD2. Уровень детальности LoD2 отображает здания в упрощенном виде. Уровень LoD2 может включать такие элементы, как стены, крыши, трубы.
В работе представлен процесс реконструкции на примере синтеза модели крыш зданий. Модели крыш зданий представлены набором полигонов. В простейшем случае будем рассматривать выпуклые полигоны. Каждый полигон может иметь разное количество сторон, в зависимости от конструкции крыш. Для распознавания и реконструкции объектов используются графы. При распознавании происходит сравнение графа объекта-эталона и графа анализируемого объекта. На место распознанного объекта помещается трехмерная параметризованная модель объекта. Таким образом, необходимо создать базу данных основных параметризованных объектов местности. Высота объектов определяется на основе карты высот, вычисленной по стереоизображениям [7]. Точки пересечения прямых линий, на которых лежат выделенные отрезки, считаются вершинами графа. Отрезки, соединяющие вершины, в рассматриваемой модели называются ребрами. При помощи простых подграфов описываются примитивы, на основе которых можно создать библиотеку трехмерных моделей крыш (табл. 1).
Модель реконструируемого объекта описывается следующим образом:
θ = {Q, H, T},
где Q – параметры контура объекта; H – высота элементов объекта; T – текстура крыши базового объекта здания. Структура контурного изображения проекции объекта определяется вектором:
Q = {Q1, Q2, ..., Qi, ..., Qn},
где Qi – точки, определяющие структуру контурного изображения. Набор отрезков, расположенных на плоскости, получается в результате векторизации изображения. Отрезки выделяются на основе преобразований Хафа. Отрезок характеризуется координатами конечных точек. Однако отрезки не всегда могут быть соединены друг с другом. Отрезки, конечные точки которых расположены на расстоянии меньше ε друг от друга, представляют собой смежные ребра графа. Вершинами графа являются точки пересечения прямых линий, которым принадлежат отрезки.
Угол между векторами, на которых лежат смежные ребра графа, не должен превышать 170°. Если угол между отрезками превышает 170° и конечные точки расположены на расстоянии меньше ε друг от друга, то такие отрезки объединяются. Конечными точками полученного отрезка становятся несмежные точки объединяемых отрезков. Также не рассматриваются отрезки, размеры которых меньше задаваемого значения.
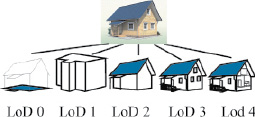
Рис. 1. Представление 3D-объекта с помощью уровней детальности по стандарту CityGML
Таблица 1
Контурные изображения крыш зданий, используемые при реконструкции
|
Номер объекта |
Трехмерная модель |
Вид сверху |
Фронтальный вид |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
Распознавание и реконструкция объектов
Предлагается описать граф с помощью матрицы смежности. Матрица смежности неориентированного графа G = (V, E) – квадратная симметричная матрица A(G) порядка n 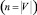 , элементы aij которой равны числу ребер, соединяющих вершины vi и vj. Сравнение графов состоит в поиске соответствий между структурами графов на основе более или менее строгих ограничений. Предлагается использовать методы сравнения на основе спектральной теории графов [8, 10, 13]. Спектр представляет множество собственных значений
, элементы aij которой равны числу ребер, соединяющих вершины vi и vj. Сравнение графов состоит в поиске соответствий между структурами графов на основе более или менее строгих ограничений. Предлагается использовать методы сравнения на основе спектральной теории графов [8, 10, 13]. Спектр представляет множество собственных значений 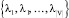 , упорядоченных по убыванию или возрастанию. Спектральные методы основаны на следующем свойстве: собственные значения и собственные векторы матрицы смежности графа инвариантны относительно перестановок вершин в матрице. Следовательно, если два графа изоморфны, их матрицы смежности будут иметь одинаковые собственные значения и векторы. Однако обратное утверждение не всегда верно: существуют графы с различными структурами, но с одинаковым спектром (коспектральные графы). Так, например, спектр графа объекта № 3 имеет вид S3 = (2,741 0,71 0,681 –0,231 –1,618 –2,22), а спектр графа объекта № 4 представлен следующим образом S4 = (3 1 0 0 –2 –2).
, упорядоченных по убыванию или возрастанию. Спектральные методы основаны на следующем свойстве: собственные значения и собственные векторы матрицы смежности графа инвариантны относительно перестановок вершин в матрице. Следовательно, если два графа изоморфны, их матрицы смежности будут иметь одинаковые собственные значения и векторы. Однако обратное утверждение не всегда верно: существуют графы с различными структурами, но с одинаковым спектром (коспектральные графы). Так, например, спектр графа объекта № 3 имеет вид S3 = (2,741 0,71 0,681 –0,231 –1,618 –2,22), а спектр графа объекта № 4 представлен следующим образом S4 = (3 1 0 0 –2 –2).
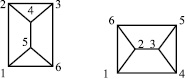
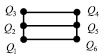
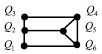
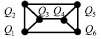
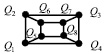
Рис. 2. Нахождение соответствий между вершинами графов
Разложение матрицы смежности на собственные значения имеет вид
A(G) = UΛUT,
где 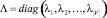 – диагональная матрица упорядоченных собственных значений;
– диагональная матрица упорядоченных собственных значений; 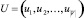 – матрица собственных векторов. Для нахождения соответствий между вершинами графов объекта-эталона и объекта на изображении используется сингулярное разложение матрицы смежности [11]. Пусть имеются графы G и Z, которые представлены на рис. 2. Необходимо найти соответствия между каждой вершиной этих графов.
– матрица собственных векторов. Для нахождения соответствий между вершинами графов объекта-эталона и объекта на изображении используется сингулярное разложение матрицы смежности [11]. Пусть имеются графы G и Z, которые представлены на рис. 2. Необходимо найти соответствия между каждой вершиной этих графов.
Матрицы смежности графов G и Z имеют вид


Выполним сингулярное разложение матриц смежности: 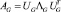 ,
, 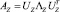 . В матрицах собственных векторов UG и UZ изменим значение отрицательных элементов, используя модуль числа. В результате разложения получим матрицы
. В матрицах собственных векторов UG и UZ изменим значение отрицательных элементов, используя модуль числа. В результате разложения получим матрицы 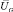 и
и 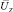 :
:
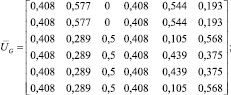
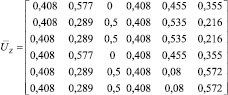
Для нахождения соответствий перемножим матрицы 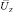 и
и 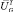 . На основе полученной матрицы сформируем матрицу перестановок P. Наибольшие значения в каждом столбце заменяются единицами, а остальные значения устанавливаются равными нулю.
. На основе полученной матрицы сформируем матрицу перестановок P. Наибольшие значения в каждом столбце заменяются единицами, а остальные значения устанавливаются равными нулю.
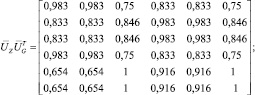








Рис. 3. Реконструкция крыш зданий: а – спутниковые снимки реконструируемых объектов; б – результаты выделения контуров с использованием преобразования Хафа; в – векторизованные изображения; г – реконструируемые модели
В полученной матрице перестановок номер столбца равен номеру узла в графе G, номер строки – номеру узла в графе Z. Единица в матрице перестановок обозначает соответствие между узлами из графа G и графа Z. Из полученной матрицы P видно, что вершине V1 графа G могут соответствовать вершины V1 и V4 графа Z, вершине V2 графа G – вершины V1 и V4 графа Z и т.д. Это объясняется тем, что структура графа симметрична. Поэтому не имеет значения, какая из двух точек будет выбрана при нахождении соответствия. В результате был осуществлен синтез трехмерной модели крыши здания (рис. 3).
Заключение
В работе был предложен подход к реконструкции трехмерных сцен города на основе распознавания спутниковых изображений с использованием спектральной теории графов. Предложена модель описания образа с использованием отрезков, объединенных в граф. Для построения графа используется информация о смежности отрезков. Для получения спектра графа используется матрица смежности. На основе рассмотренного подхода можно распознать основные типы крыш зданий. Однако существуют крыши сложного типа, которые можно получить на основе базовых моделей. Дальнейшие исследования будут направлены на разработку алгоритмов для реконструкции сложных 3D-моделей крыш на основе предложенного подхода.
Работа выполнена при поддержке гранта РФФИ 15-07-01612-А, задания на выполнение государственных работ в сфере научной деятельности в рамках базовой части государственного задания Минобрнауки России (проект № 2918).
Рецензенты:
Жизняков А.Л., д.т.н., профессор, первый зам. директора, МИ (ф) ВлГУ, г. Муром;
Орлов А.А., д.т.н., доцент, зав. кафедрой физики и прикладной математики, МИ (ф) ВлГУ, г. Муром.
Работа поступила в редакцию 17.04.2015.