В современном строительстве в значительных объемах используются бетоны. 2 млрд м3 в год – таков сегодня мировой объем его применения [1]. В настоящее время в строительстве применяются более тысячи различных видов бетона, и процесс создания их новых видов интенсивно продолжается. Это касается в первую очередь материалов, используемых в конструкциях, работающих в условиях воздействия высоких температур, динамических нагрузок, ионизирующих излучений.
К таким материалам, обладающим свойствами, превышающими показатели традиционных материалов (бетонов, полимербетонов), относятся бетоны на металлических связующих и гранулированных заполнителях – металлобетоны (метоны), предложенные профессором В.И. Соломатовым. В металлобетонах в качестве связующих используются алюминий, сталь, чугун, титан, медь, свинец, олово, цинк и др., а заполнителей – песок, щебень, гравий, керамзит и др. [13]. Получают металлобетоны (метоны) объединением компонентов при температуре расплава соответствующего металла (связующего), распалубливанием и извлечением изделий из формы после остывания металла. Металлобетоны имеют специфические показатели структуры и свойств, что требует проведения расчетно-экспериментальных методов их изучения.
Моделирование долговечности металлобетонов с учетом накопления повреждений
В последние годы широкое распространение получили модели и теории длительной прочности, учитывающие накопление повреждений [2, 3, 6, 7, 8, 10, 11, 14]. Разрушение в этом случае представляется в виде необратимого кинетического процесса накопления повреждений в материале, ускоряемого температурой. В работах [2, 3] предложена математическая модель процесса разрушения композиционных материалов со случайной структурой. Для случая одноосного сжатия применен подход, в котором введен параметр повреждаемости ξ = 1 – n [12]. При этом принято, что скорость роста параметра повреждаемости зависит только от значений σ и φ в данный момент. Так как значение φ в процессе разрушения меняется от 1 до 0, время до разрушения рассчитывается из уравнения
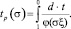 (1)
(1)
Величине ξ придается некоторый физический смысл, например, относительное количество неразрушенных связей в материале.
Поэтапно примем:
1) ξ = φ(σ) и σ = const;
тогда 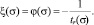 (2)
(2)
2) Если величина σ меняется во времени σ = σ(t), тогда
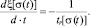 (3)
(3)
Из последнего уравнения следует известная формула линейного суммирования повреждений:
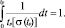 (4)
(4)
Деформации находятся независимо от расчета долговечности при условии принятия некоторой гипотезы «о» связи величин ε и ξ. Допуская, что все связи упругие и приписывая параметру повреждений упомянутый физический смысл, приходим к простой формуле
ε = σ/(Eξ). (5)
Прочность метона как многокомпонентной системы зависит от многих структурообразующих факторов. В первую очередь к ним необходимо отнести объемное содержание заполнителя, прочность матрицы и заполнителя, прочность связи на границе «металл-заполнитель».
Разрушение метона – сложный процесс, который складывается из разрушения матрицы, заполнителя и связи на границе раздела фаз. Общая работа разрушения метона будет состоять из трех слагаемых:
GK = GM + GЗ + GРС, (6)
где GK, GM, GЗ, GРС – соответственно энергии разрушения композита, матрицы, заполнителя и связи «металл – заполнитель».
Предположим, что заполнитель крупностью d имеет расстояние между зернами – x. Считаем, что область пластической деформации в матрице имеет треугольную форму. Тогда объем заполнителя будет равен
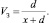 (7)
(7)
Объем материала, деформируемого на единицу площади распространяющейся трещины, согласно [11] будет равен
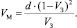 (8)
(8)
Работа разрушения единичного объема матрицы находится:
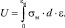 (9)
(9)
С учетом (7) и (8) работа разрушения матрицы будет
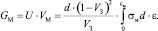 (10)
(10)
Работа, связанная с разрушением заполнителя, может быть оценена следующим выражением:
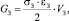 (11)
(11)
где σз – прочность заполнителя; εз – деформация заполнителя.
В результате химического взаимодействия фаз на поверхности заполнителя образуются хрупкие продукты реакции типа интерметаллидов. В процессе работы метона этот слой растрескивается. Работа, связанная с разрушением этого слоя, будет равна
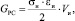 (12)
(12)
где σи – прочность интерметаллида; Vи – толщина слоя интерметаллида; εи – деформация интерметаллида.
Подставив значения и выполнив преобразования, получим
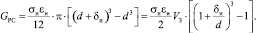 (13)
(13)
Общая работа разрушения метона будет определяться следующим выражением:
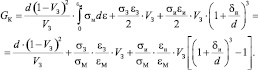 (14)
(14)
Таким образом, видно, что прочность метона зависит от крупности и прочности заполнителя и толщины границы раздела «металл – заполнитель». При увеличении крупности и прочности заполнителя, толщины интерметаллида прочность композита возрастает.
При растяжении композита из метона механизм разрушения иной, чем при сжатии. В силу недостаточно высокой прочности границы раздела «металл – заполнитель» последний практически не влияет на прочность метона. Прочность метона при растяжении определяется прочностью матрицы, а заполнитель в этом случае является как бы дефектом композита. Таким образом, при слабом контакте металл – заполнитель заполнитель можно рассматривать как дефект размером d. Тогда энергия разрушения композита будет равна
GК = GМ + GРС. (15)
При наличии дефекта энергия разрушения в матрице определится выражением
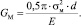 (16)
(16)
Тогда
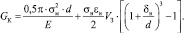 (17)
(17)
Таким образом, видно, что при увеличении дефекта (крупности заполнителя) энергия разрушения в матрице возрастает, а напряжения, необходимые для разрушения матрицы, снижаются.
Известно, что упрочняющие частицы в композиционных материалах выполняют ту или другую из двух возможных функций. Во-первых, если матрица пластична и претерпевает большую пластическую деформацию, то жесткие, упрочняющие частицы блокируют движение дислокаций или скольжение, ограничивая тем самым пластическую деформацию. Во-вторых, если матрица хрупкая и разрушается путем распространения уже существующих трещин, то упрочняющие частицы ограничивают размеры исходных трещин в хрупкой матрице и тем самым определяют уровень прочности.
Таким образом, в аспекте кинетической концепции разрушения макропроцесс разрушения металлобетона состоит из ряда стадий: деформации связей между компонентами под нагрузкой, разрыва связей, зарождения трещин на границе раздела, в металлическом связующем или заполнителях.
Ниже рассматриваются факторы, которые могут способствовать возникновению повреждений, усадка и механические нагрузки.
Моделирование структурных напряжений в металлобетонах
На стадии изготовления и во время эксплуатации в структурных элементах композиционных материалов возникают напряжения, которые называют структурными. На начальной стадии формирования металлобетонов структурные напряжения вызываются усадкой. Усадка отливок из метона происходит вследствие охлаждения металла от температуры расплава до конечной температуры. Температурная зависимость изменения объема металла может быть записана в следующем виде:
VК = VП·[1 – α0(tП – tК)], (18)
где VП – первоначальный объем сплава при температуре tП; VК – конечный объем сплава при температуре tК; α0 – средний коэффициент температурного сжатия в интервале температур (tП – tК).
Развитию усадочных деформаций в композитах препятствует заполнитель. Вследствие этого в композите возникают структурные напряжения. Заполнитель, обладающий меньшим коэффициентом термического сжатия, будет сжиматься, а в матрице возникнут растягивающие напряжения. Такое напряженное состояние может привести к появлению микротрещин в матрице или заполнителе. Поэтому при изготовлении изделий из композиционных материалов необходимо учитывать усадку материала матрицы и коэффициенты термического расширения компонентов при их совместной работе.
Разность деформаций усадки матрицы и заполнителя равна разности коэффициентов термического сжатия металла (αМ) и заполнителя (αЗ), умноженной на интервал температур, при котором происходит усадка:
Δε = (αМ – αЗ)·Δt. (19)
Представим метон как двухкомпонентный материал, состоящий из шаровидных заполнителей со сферической оболочкой (рис. 1).
Выражения структурных напряжений в такой модели находятся путем решения задачи Ляме об упругой сфере, находящейся под действием внутреннего и внешнего давления:
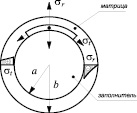
Рис. 1. Структурный элемент метона
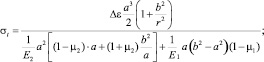 (20)
(20)
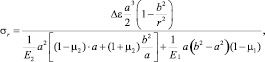 (21)
(21)
где σt и σr – тангенциальные и радиальные напряжения; a – радиус поперечного сечения заполнителя; b – общий радиус поперечного сечения структурного элемента; r – текущая радиальная координата; E1; µ1 – модули Юнга и Пуассона заполнителя; Е2, µ2 – модули Юнга и Пуассона матрицы.
Таблица 1
Физико-механические свойства компонентов металлобетона
|
№ п/п |
Компоненты |
Прочность при сжатии, МПа |
Модуль упругости, МПа |
Коэффициент Пуассона |
Коэффициент температурного расширения, 1/К°∙105 |
|
1 |
Алюминиевый сплав (АЛ2) |
250 |
72000 |
0,3 |
2,28 |
|
2 |
Серый чугун (СЧ-20) |
510 |
115000 |
0,22 |
1,04 |
|
3 |
Конструкционный алюминиевый чугун (КАЧ) |
480 |
90000 |
0,24 |
1,2 |
|
4 |
Фарфоровые шарики диаметром 10 мм |
40000 |
0,22 |
0,3 |
|
|
5 |
Фарфоровые шарики диаметром 6 мм |
42000 |
0,22 |
0,3 |
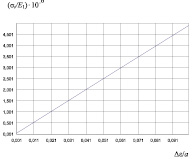
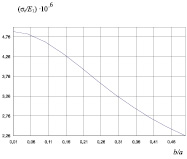
а б
Рис. 2. Зависимости изменения относительного показателя тангенциальных напряжений в заполнителе металлобетона от величины относительных деформаций в металлобетоне (а) и толщины прослойки матрицы (б)
Проведена оценка влияния структурообразующих факторов на величину и характер изменения структурных напряжений в радиальном и тангенциальном направлениях. В качестве вяжущих (матрицы) были приняты литейный алюминиевый сплав АЛ2, серый чугун СЧ-20 и конструкционный алюминиевый чугун (КАЧ), а в качестве крупного заполнителя – фарфоровые шарики диаметром 10 и 6 мм. Физико-механические свойства составляющих компонентов металлобетона приведены в табл. 1.
В ходе исследований структурных напряжений в металлобетонах проводилась оценка влияния размера (радиуса) структурного элемента металлобетона (зависимого от крупности заполнителя); оценка влияния величины относительных деформаций в металлобетоне и деформативных свойств матрицы на величину и характер изменения структурных напряжений в радиальном и тангенциальном направлениях. Структурные напряжения определены при фиксированных значениях показателей компонентов металлобетонов (в том числе толщины прослойки матрицы b/а = 0,01–0,5; усадки структурных компонентов Δε/а = 0,001–0,01; характеристики деформативных свойств структурных компонентов Е2/Е1 = 0,25–2,5; отношения коэффициентов Пуассона матрицы и заполнителя в пределах μ2/μ1 = 0,1–0,5. В качестве заполнителя принимались фарфоровые шарики диаметром 10 мм и имеющие модуль деформации – 40000 МПа. При моделировании варьировались деформативные свойства приведенной металлической матрицы (в пределах 10000–100000 МПа).
На основе проведенных расчетов при использовании фиксированных значений показателей компонентов металлобетонов (Δε/а, b/а) построены графические зависимости изменения отношения тангенциальных напряжений к модулю деформации заполнителя (σt/Е1) в металлобетоне (рис. 2).
Из результатов исследований следует, что максимальные структурные напряжения возникают на контакте более жесткой матрицы с заполнителем. Они могут привести к разрыву оболочки от тангенциальных напряжений. Матрица из конструкционного алюминиевого чугуна ведет себя более пластично, и тангенциальные напряжения имеют более низкие значения. При использовании матрицы из алюминиевого сплава с большей пластичностью структурные напряжения при охлаждении композита являются незначительными.
Отсюда можно сделать вывод, что с целью снижения структурных напряжений в металлобетоне необходимо характеристики деформативности (Е и µ) металла и заполнителей подбирать в определенных соотношениях.
Исследование напряженно-деформируемого состояния (НДС) металлобетонов при нагружении
1. Методика для анализа НДС
Известно, что выявление распределения напряжений и деформаций в композиционных материалах связано со значительными трудностями, обусловленными их специфической структурой и условиями нагружения. Поэтому в приближенных расчетах часто используют упрощенные модели в сочетании с экспериментальными методами тестирования, например метод конечных элементов. В качестве средства анализа НДС в данной работе использовалась методика численного моделирования [4]. В соответствии с методикой численного моделирования разрабатывается план опытного эксперимента для получения необходимых расчетных данных при использовании программного комплекса [5].
Программным комплексом предусматривается варьирование следующих факторов: вид и свойства зернистых включений и матрицы, размер фрагментов разрушения, критериев разрушения образцов и компонентов структуры. В процессе моделирования разрушения образцов методом итераций осуществляется подбор механических параметров компонентов. В процессе пошаговых итераций варьируются последовательно деформативные и прочностные параметры включений, зон матрицы когезии и адгезии. Условием итерации является равенство механических параметров объектов, найденных опытным путем и численным моделированием. Численные значения показателей компонентов в дальнейшем используются как параметры численного моделирования. Компоненты в структуре размещаются при помощи датчика случайных чисел согласно плану эксперимента. Интерфейсы (зоны взаимодействия) определяются соответствующими включениями: область когезии – внешняя оболочка включения, область адгезии – внешняя оболочка включения внутри матрицы.
Для формирования расчетных моделей используется плоское напряженно-деформируемое состояние объекта. Программа включает следующие функциональные блоки [5] формирования базы матриц жесткости исходной конечно-элементной модели, ее последующую поэтапную фрагментацию (степень фрагментации определяется минимальным размером элементарного фрагмента деформирования и разрушения); формирования структуры металлобетона (размещение включений с учетом их объемного удельного содержания и оболочек включений); формирования параметров состояния структуры на пути разрушения; циклического моделирования поэтапного деформирования и разрушения объектов (определение модуля обратимой деформации, прочности на сжатие компонентов (матрицы и заполнителей) методом итераций для каждого пункта плана экспериментальных работ) тестирования найденных параметров численным моделированием комплексных объектов, содержащих совокупность включений и определение корректировочных коэффициентов, учитывающих структурные взаимодействия между ними; прогнозирования значения модуля деформации и прочности на сжатие оптимизируемого состава металлобетона; интерполяции и экстраполяции механических параметров модифицируемых составов металлобетонов; формирования и вывода файлов результатов численного моделирования.
Следует отметить, что термины параметров компонентов (матрица, включения, когезия и адгезия), имеют условное значение и действуют только применительно к рассмотрению структуры объекта моделирования при анализе структурных взаимодействий. Суть их заключается в математическом решении и проведении анализа системой численного моделирования состояния объекта и его изменения при приложении нагрузки и разрушении. Это состояние и выражается интерпретированными значениями механических параметров. На основе проведенных вычислений аналитическими методами система переходит к определению параметров объекта моделирования модифицируемого материала, состав которого был принят в соответствии с планом намеченных исследований.
При определении механических свойств составов металлобетонов устанавливаются зависимости прочности и деформативности от вида матрицы, содержания и крупности зерен заполнителя. В процессе определения механических параметров компонентов одновременно проводится и анализ структурных взаимодействий между ними. Системой численного моделирования определяется характер разрушения объекта и выявляется наиболее слабый структурный компонент.
2. Исследование НДС металлобетонов с прочными заполнителями
В качестве исходных расчетных данных принимались результаты лабораторных испытаний образцов составов металлобетонов с матрицей из серого чугуна марки СЧ-20 (ГОСТ 1412-85) и конструкционного алюминиевого чугуна марки КАЧ (ГОСТ 1412-70). Объектом моделирования являлся куб с размером ребра 4 см, геометрически подобный опытному образцу при лабораторных испытаниях. Модуль упругости и прочность на сжатие матриц и заполнителей, а также физико-механические параметры объектов исследований приведены в табл. 2.
На рис. 3 и 4 приведены зависимости изменения прочности на сжатие и модуля деформации металлобетонов на сером и алюминиевом чугуне от степени наполнения фарфоровыми шариками различных диаметров, а также базальтовым и диабазовым щебнем, полученные при помощи численного моделирования.
Таблица 2
Исходные расчетные данные для моделирования
|
Номер состава |
Ес.ч, МПа |
Rс.ч, МПа |
Ек.а.ч, МПа |
Rк.а.ч, МПа |
Езап, МПа |
Rзап, МПа |
Механические параметры объекта |
|
|
Ео, МПа |
Rо, МПа |
|||||||
|
Заполнитель – фарфоровые шарики диаметром 10 мм |
||||||||
|
1 |
115000 |
510 |
– |
– |
40000 |
38 |
88500 |
480 |
|
2 |
– |
– |
90000 |
480 |
40000 |
38 |
83600 |
510 |
|
Заполнитель – фарфоровые шарики диаметром 6 мм |
||||||||
|
3 |
115000 |
510 |
– |
– |
42000 |
40 |
90000 |
490 |
|
4 |
– |
– |
90000 |
480 |
42000 |
40 |
84000 |
520 |
|
Заполнитель – диабазовый щебень |
||||||||
|
5 |
115000 |
510 |
– |
– |
50000 |
48 |
85000 |
420 |
|
6 |
– |
– |
90000 |
480 |
50000 |
48 |
80000 |
510 |
|
Заполнитель – базальтовый щебень |
||||||||
|
7 |
115000 |
510 |
– |
– |
32000 |
38 |
87000 |
410 |
|
8 |
– |
– |
90000 |
480 |
32000 |
38 |
81000 |
490 |
Рис. 3. Зависимость изменения прочности на сжатие металлобетонов на сером (1) и алюминиевом чугуне (2) от степени наполнения различными заполнителями: а – фарфоровыми шариками диаметром 10 мм; б – фарфоровыми шариками диаметром 6 мм; в – диабазовым щебнем; г – базальтовым щебнем
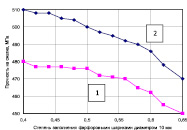

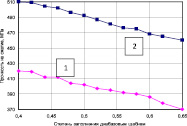


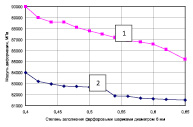

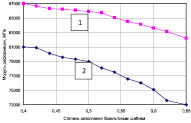
Из графиков следует, что с увеличением объемного содержания заполнителя модули деформации композитов на сером и алюминиевом чугуне несколько сближаются. При этом повышение содержания фарфоровых шариков приводит к значительному снижению жесткости металлобетона. Также видно, что при увеличении степени наполнения заполнителем происходит снижение прочности и модуля деформации металлобетона. В смеси с плавающим заполнителем без контактных зон (менее 50 % по объему) зерна заполнителя раздвинуты и не взаимодействуют между собой, оказывают влияние только на прилегающую зону металла. С увеличением степени наполнения (50–65 % по объему) создаются зоны взаимодействия оболочек адгезии (интерфейсы) отдельных зерен заполнителя, перекрывающих друг друга, а матрица в виде тонких металлических пленок обволакивает частицы, не прерываясь. При степени наполнения до 50 % разрушению подвергается металлическая матрица. Критическая нагрузка, приложенная к образцу, ведет к разрушению металлической прослойки и объекта в целом. В данном случае разрушение начинается сколом материала в частной зоне. При дальнейшем увеличении содержания заполнителя нагрузка воспринимается и более слабым компонентом – фарфоровыми шариками или зернами щебня.
Следует отметить, что установленные численным моделированием, данные повышения прочности при увеличении содержания металла и уменьшении прочности при увеличении содержания менее прочного заполнителя, а также разграничения напряжений в металлобетоне по зонам при поэтапном разрушении, соответствуют теории прочности бетонов на цементном связующем.
3. Исследование НДС металлобетонов с малопрочными заполнителями
По аналогичной методике нами проведены исследования механических свойств металлобетонов на матрице из серого чугуна марки СЧ-20 (с начальными данными Ес.ч = 115000 МПа и Rс.ч = 510 МПа) и легкого заполнителя. При моделировании такие композиты представлены как сплошная среда с включениями в виде макропор из-за малой прочности легких заполнителей. Проводились исследования характера разрушения структуры в зависимости от скорости нагружения и размеров макропор. С увеличением размеров макропор от начальных заданных значений размеров пор, рассматриваемых как включения, увеличивается и степень концентрации напряжений, а с увеличением скорости приложения нагрузки, превышающей скорость разрушения металлической матрицы, на каждом этапе разрушения увеличивается зона разрушения или обобщенный фрагмент разрушения. Он включает все одновременно разрушаемые области на каждом этапе разрушения (процесс разрушения рассматривается поэтапно).
В качестве объекта моделирования принят образец кубической формы размером 10×10×10 см. Численное моделирование структуры однородной металлической матрицы выполнялось также с использованием разработанной методики. Размещение макропор при формировании структуры объекта моделирования реализуется на основе использования датчика случайных чисел. В качестве основы формирования структуры модели использовалась, конечно-элементная модель, получаемая на основе поэтапной фрагментации треугольных конечных элементов. При выполнении исследований варьировалось число циклов фрагментации (при моделировании принимается 4, 5, 6, 7, 8-кратная разбивка каждого элементарного фрагмента разрушения). То есть элементарный фрагмент разрушения определен как конечный элемент последнего этапа фрагментации. Размер макропор определен номером этапа фрагментации. Обобщенный фрагмент разрушения включает элементарные фрагменты разрушения, размещенные компактно или разрозненно в пределах всего объекта моделирования.
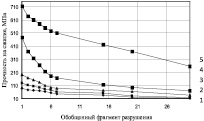
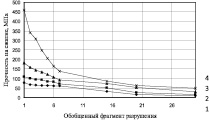
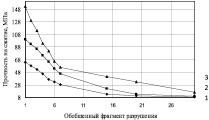
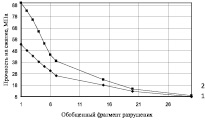
На рис. 5 приведены диаграммы зависимости прочности металлической матрицы при числе циклов фрагментации конечно-элементной модели объекта (для варианта «а» равном 8, «б» – 7, «в» – 6, «г» – 5). На всех диаграммах рис. 5 показаны графики зависимостей для размеров пор, определенных конечным элементом номером последнего этапа фрагментации, таким образом, графикам 1, 2, 3, 4, 5 соответствуют номера этапов фрагментации конечных элементов – 4, 5, 6, 7, 8. При моделировании принято минимальное условное значение эффективного диаметра пор – 0,78 мм (при цикле фрагментации объекта моделирования – 8), максимальное условное значение – 12,5 мм (при цикле фрагментации объекта моделирования – 4).
а б
в г
Рис. 5. Диаграммы зависимости прочности металлической матрицы при числе циклов фрагментации конечно-элементной модели объекта: «а» равном 8, «б» – 7, «в» – 6, «г» – 5, где номер графика соответствует размерности пор
Из графических зависимостей следует, что с увеличением количества конечных элементов обобщенного фрагмента разрушения прочность металлической матрицы, отвечающая опытной прочности образца выплавленного из серого чугуна, уменьшается по логарифмической зависимости. Это может быть интерпретировано как зависимость прочности объекта от скорости нагружения на каждом этапе формирования пути разрушения. С увеличением размеров пор прочность матрицы уменьшается в связи с увеличением интенсивности концентрации напряжений. С уменьшением разбивки конечно-элементных моделей (уменьшением числа циклов фрагментации на диаграммах (а–г) (рис. 5 – с 8 до 4) значение прочности на сжатие металлической матрицы уменьшается. На основе полученных результатов для выполнения численного моделирования рекомендуется обощенный фрагмент разрушения принимать равным – 7, при котором прочность матрицы для наиболее мелких пор (при цикле фрагментации равном – 8) получена равной 510,7 МПа (рис. 5, а). Таким образом, значение прочности на сжатие объекта моделирования соответствует опытным данным при количестве обобщенного фрагмента разрушения равного – 7.
Выводы
1. Выполнено экспериментально-теоретическое обоснование создания металлобетонов (материалов на основе металлических связующих и гранулированных заполнителей с улучшенной структурой и повышенной долговечностью).
2. Разрушение металлобетонов рассматривается как процесс накопления повреждения в матрице, заполнителях и на границе разделе фаз. Процессы накопления повреждений определяются усадочными и механическими факторами, напряженно-деформированным состоянием композита.
3. Проведена оценка влияния структурообразующих факторов на величину и характер изменения структурных напряжений в металлобетонах на основе алюминиевого чугуна. Структурные напряжения понижаются на контакте матрицы и заполнителей к ряду: серый чугун, алюминиевый чугун, алюминиевый сплав.
4. Исследовано напряженно-деформируемое состояние металлобетонов с прочными и малопрочными заполнителями при нагружении методом численного моделирования. Показано, что с увеличением степени наполнения происходит снижение прочности и модуля деформации металлобетона. При использовании пластичной матрицы заполнители блокируют движение дислокаций или скольжение, ограничивая тем самым пластическую деформацию. Если матрица жесткая, разрушение идет за счет распространения трещин.
Печатается при поддержке гранта РФФИ № 13-08-971-71 «Исследование в области создания новых полимербетонов, каркасных фибробетонов, бетонов различного фракционного состава с биоцидными добавками для организации промышленного производства строительных изделий с повышенной долговечностью, биологической и климатической стойкостью на предприятиях Республики Мордовия и гранта РФФИ № 13-08-97175 «Исследование характера разрушения типовых элементов бетонных конструкций с продольной и поперечной арматурой из металла и высокопрочных крепежных элементов из полимерных композиционных материалов при воздействии приморского климата и морской воды».
Рецензенты:
Хвастунов В.Л., д.т.н., профессор кафедры «Технология строительных материалов и деревообработки», Пензенский государственный университет архитектуры и строительства, г. Пенза;
Рыжаков В.В., д.т.н., профессор, зав. кафедрой «Техническое управление качеством», Пензенский государственный технологический университет, г. Пенза.
Работа поступила в редакцию 17.04.2015.



