Физической предпосылкой к улучшению характеристик системы обмена данными (СОД), осуществляющей при управлении воздушным движением (УВД) с автоматическим зависимым наблюдением (АЗН) передачу навигационных данных с борта ВС в дифференциальную подсистему (ДП) и корректирующей информации при дифференциальном режиме работы аппаратуры потребителей спутниковой радионавигационной системы (АП СРНС), путем комплексирования радиоприемных устройств (РПУ) СОД и АП СРНС, является наличие функционально связанных параметров связных и навигационных сигналов и информационная избыточность навигационных измерений.
Уравнения наблюдения на связном и навигационном входах комплексированного РПУ, соответственно, записываются:
ξ1(t) = s1(t, λ, θ) + n1(t); (1)
ξ2(t) = s2(t, λ) + u(t). (2)
Здесь s1(t, λ, θ) – связной сигнал, зависящий как от вектора непрерывных параметров λ, так и от дискретного параметра θ, несущего информацию о передаваемом сообщении.
Рассмотрим случай использования бинарного фазоманипулированного сигнала (ФМ-2), обеспечивающего, как известно, наиболее высокую помехоустойчивость канала связи. При этом он запишется как
s1(t, λ, θ) = U0 f(t – τ) θ(t – τ) cos (wot +φ), (3)
где U0 – амплитуда сигнала, f(t – τ) и θ(t – τ) – псевдослучайные последовательности (ПСП) и символы модуляции сигнала данными передаваемого сообщения, а вектор непрерывных параметров λ включает в себя случайные фазу φ, задержку τ и доплеровскую частоту ω сигнала. Поступающий с выхода АП СРНС сигнал s2(t, λ) содержит укороченный вектор непрерывных параметров
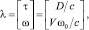(4)
где D – расстояние между РПУ и радиопередающим устройством (РПДУ); V – радиальная скорость ВC; ω0 – несущая частота сигнала; с – скорость распространения радиоволн.
Шум наблюдения в связном канале n1(t) полагаем белым гауссовым с нулевым математическим ожиданием и спектральной плотностью N1/2, а шум наблюдения в навигационном канале u(t) – окрашенным. Процессы λ(t) и u(t) полагаем марковскими, описываемыми стохастическими дифференциальными уравнениями, которые могут быть представлены в виде
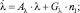(5)
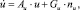(6)
где
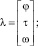
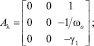
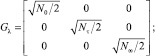
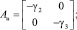
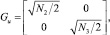
где γi и Ni – соответствующие коэффициенты сноса и спектральные плотности.
Априорные уравнения (5), (6) и уравнения наблюдения (1), (2) позволяют с использованием марковской теории оптимальной нелинейной фильтрации (ОНФ) синтезировать квазиоптимальные алгоритмы комплексной обработки дискретно-непрерывной информации системы связи совместно с выходными сигналами АП СРНС [2, 3], а затем с помощью стохастического моделирования на ЭВМ получить точностные и динамические характеристики синтезированной системы и сравнить их с аналогичными характеристиками некомплексированной системы.
В рамках гауссовой аппроксимации апостериорной плотности вероятностей вектора непрерывных параметров λ [4], позволяющей перейти к приближенным соотношениям для математического ожидания λ и вторых центральных моментов R аппроксимирующего гауссова распределения, квазиоптимальные алгоритмы фильтрации дискретно-непрерывных параметров имеют вид [5]
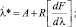(7)
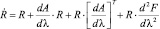. (8)
Коэффициенты этих уравнений в случае, когда одна часть наблюдений проводится на фоне белых, а другая часть – на фоне окрашенных шумов наблюдения, определяются соотношениями [1]
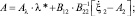(9)
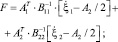(10)
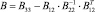, (11)
где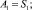 
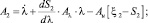
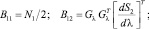
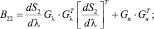
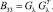
При этом уравнение для вычисления вектора оценок имеет вид
(12)
где
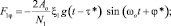
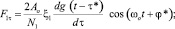
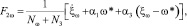
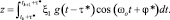
Оценка дискретного параметра θ на k-м тактовом интервале производится в соответствии с алгоритмом: z >< 0. Отличие комплексированного алгоритма от некомплексированного заключается в том, что для последнего в уравнении (12) следует положить F2τ = F2ω = 0.
Был проведен сравнительный анализ этих алгоритмов путем их стохастического моделирования на ЭВМ. На рис. 1 приведены зависимости вероятности ошибочного приема дискретного параметра θ, которая определялась как зависимость относительной частоты несовпадений оценочных значений θ* с истинными значениями от отношения сигнал/шум на тактовом интервале q = A0 T0/N1.
Как видим, при большом значении q обе кривые мало различимы, а при приближении к пороговому значению q вероятность ошибочного приема в комплексированной системе (кривая 1) значительно меньше, чем в некомплексированной (кривая 2), что может быть объяснено проявлением эффекта «перескоков фаз», связанного с полимодальностью апостериорного распределения фазы.
На рис. 2 приведены зависимости от q выигрыша в дисперсии оценки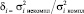 
непрерывных параметров φ, τ, ω при переходе от некомплексированной к комплексированной системе.
Из анализа этих зависимостей видно, что выигрыш существенен, особенно при приближении к пороговому значению q.
На рис. 3 приведены зависимости дисперсии оценки частоты от времени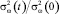 
для комплексированной (кривая 1) и некомплексированной (кривая 2) систем.
Как видно из этих зависимостей, комплексирование существенно улучшает динамические характеристики системы.
Таким образом, использование навигационной поддержки от АП СРНС позволяет существенно повысить достоверность передачи данных по каналу связи. При этом улучшение точностных и динамических характеристик систем слежения за непрерывными параметрами связного сигнала свидетельствует об улучшении указанных характеристик системы синхронизации СОД. Причем, поскольку частота и задержка сигнала s1(t, λ, θ) к началу сеанса связи известны с достаточной точностью на основании данных, получаемых с выхода АП СРНС, в канале синхронизации возможно исключение режима поиска сигнала.
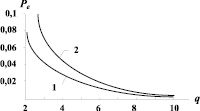
Рис. 1. Зависимость вероятности ошибки от отношения сигнал/шум для комплексированной (кривая 1) и некомплексированной (кривая 2) систем
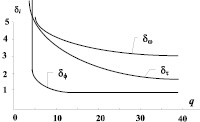
Рис. 2. Зависимость выигрыша дисперсии оценки непрерывных параметров от отношения сигнал/шум
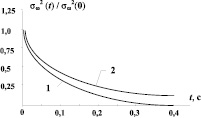
Рис. 3. Зависимость дисперсии оценки частоты от времени в комплексированной и некомплексированной системах
Рецензенты:
Козлов А.И., д.ф.-м.н., профессор, «Техническая эксплуатация радиоэлектронного оборудования воздушного транспорта», Московский государственный технический университет гражданской авиации, г. Москва;
Акиншин Р.Н., д.т.н., доцент, ведущий научный сотрудник секции по оборонным проблемам Министерства обороны (при Президиуме Российской академии наук), г. Москва.
Работа поступила в редакцию 17.04.2015.