Современные достижения в области информационных технологий актуализировали задачу защиты конфиденциальных сведений от конкурентной разведки. По оценкам зарубежных и отечественных аналитиков до 90 % конфиденциальных сведений может быть получено из открытых источников путем проведения информационно-аналитической работы с ними [1, 3]. Там же приводятся методы работы конкурентной разведки по получению таких сведений из открытых источников информации. Вся задача информационно-аналитической службы конкурента состоит в том, чтобы быстрее найти необходимую информацию в открытых источниках и правильно ее проанализировать для получения конфиденциальных сведений. Разведывательный цикл обработки информации состоит по крайней мере из четырех значимых по временным затратам этапов: постановка компанией задачи, процесс сбора информационных сведений, сортировка, обработка и оценка собранных информационных сведений и наконец анализ собранных информационных сведений и создание на их основе информационных данных, пригодных для выработки управленческого решения [2]. Задачей системы противодействия конкурентной разведке является выбор такого метода защиты сведений из множества возможных методов (с учетом допустимых ограничений на собственные ресурсы), который максимизирует время работы информационно-аналитической службы конкурента по сбору и анализу информации в открытых источниках [5]. Одна из известных моделей противодействия конкурентной разведке – это маскировка конфиденциальных сведений в открытых источниках. Этот метод затрудняет распознавание конфиденциальных сведений на фоне множества открытых сведений путем изменения информационного образа на семантическом уровне. Возможны следующие способы изменения информационного образа [4, 7]:
1) удаление части элементов и связей, образующих информационный узел (наиболее информативную часть) информационного образа;
2) изменение части элементов информационного образа при сохранении связей между оставшимися элементами;
3) удаление или изменение связей между элементами информационного образа при сохранении их количества.
Цели и методы
Целью работы является изучение возможностей методов линейного программирования для оптимизации использования маскировки конфиденциальных сведений.
Предположим, имеется некоторое множество информационных образов X[i]:
X[1]: «компания собирается купить новое оборудование»;
X[2]: «для производства нового товара»;
X[3]: «на сумму 200000 рублей».
Все образы абсолютно достоверны. Обозначим это следующим образом:
X[1] = 1; X[2] = 1; X[3] = 1.
Тогда информационный образ всего конфиденциального сообщения «Компания собирается купить новое оборудование для производства нового товара на сумму 200000 рублей», которое необходимо замаскировать, чтобы скрыть его абсолютную достоверность, можно представить так:
X = X[1]∩X[2]∩X[3] = 1.
При проведении маскировки первым способом необходимо удалить часть элементов и связей, образующие сообщение. При удалении X[1] мы получим замаскированное сообщение K1 «Компания потратит 200000 рублей на производство нового товара»:
K1 = X[2]∩X[3] = 1.
Удалив X[2], получим K1 «Компания собирается купить новое оборудование на сумму 200000 рублей»:
K1 = X[1]∩X[3] = 1.
Наконец, удалив X[3], получим K1 «Компания собирается купить новое оборудование для производства нового товара»:
K1 = X[1]∩X[2] = 1.
Отметим, что полученные высказывания K1 также будут абсолютно достоверными, что позволит им беспрепятственно быть принятыми информационно-аналитической разведкой конкурента, однако относительно искомого сообщения X они будут менее полными. Данный способ является ярким примером недосказанности.
Предположим теперь, что маскировка будет проводиться вторым способом путем преувеличения или преуменьшения высказывания X. То есть к информационному образу X будут добавляться заранее недостоверные сведения N[i]. Следовательно, получим новое высказывание K2 которое будет складываться из нескольких X[i] и N[i].
Итак, замаскируем сообщение путем преувеличения, преуменьшения или изменения части этого сообщения (применим функцию шифрования). Заменим высказывание X[2] ложным, а высказывание X[3] преувеличим. Новое высказывание K2: «Компания собирается купить новое оборудование для замены старого на сумму 300000 тысяч рублей». Данное высказывание не полностью достоверно, степень достоверности уменьшается с каждой заменой составляющих элементов, однако преувеличение или преуменьшение влияют меньше, чем замена истинного элемента ложным.
Используя третий способ маскировки, изменим логические связи между элементами сообщения X. Тогда высказывание K3 может принять следующий вид: «Может быть, компания потратит 200000 тысяч рублей на покупку нового оборудования в ближайшее время или же займется выпуском новой продукции». Данное высказывание содержит достаточно достоверные сведения, но не однозначно, истинность высказываний X[3] и X[1] будет под сомнением. Формализация будет зависеть от контекста, в котором сообщение будет представлено. В данном сообщении говорится о том что, может быть, компания потратит 200000 тысяч рублей на покупку оборудования, в противном же случае займется выпуском новой продукции. То есть высказывание Z «может быть» будет влиять на степень достоверности высказывания K3. Видно, что в K3 заменена связь между элементами «и» на «или»:
K3 = Z∩(X[3]∩X[1])∪X[2].
Ко всему сказанному нужно добавить, что комбинирование рассмотренных трех методов также возможно. Поэтому интересно выяснить – как добиться максимальной эффективности маскировки при использовании этих методов и ограничениях на расходы, затрачиваемые на маскировку.
Итак, опять предположим, что имеется некоторое множество информационных образов X и информационные образы K1, K2 и K3. Конкурентная разведка стремится выявить образы X и использовать конфиденциальные сведения в своих целях, тогда как информационные образы K1, K2 и K3 ее не интересуют. Из изложенного выше известно, что i-е образы X маскируются под образы Ki, i = 1, 2, 3. Для общности введем еще одну часть образа X[4], которая вообще не маскируется. Следуя [6], будем считать, что
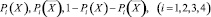
обозначают вероятности того, что при i-м способе маскировки конкурентная разведка, столкнувшись с информационным образом X:
/1/ правильно определит его тип;
/2/ ошибочно будет считать, что это не X, то есть K1 или K2, или K3;
/3/ не примет никакого определенного решения.
Тогда, если C1, C2, C3 представляют независящие от способов маскировки величины наших выигрышей в каждом из случаев /1/, /2/, /3/, то
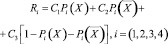 (1)
(1)
есть средний выигрыш на одно решение при i-м способе маскировки.
Обозначим через x1, x2, x3, x4 частости, с которыми применяется каждый из способов маскировки, а через a1, a2, a3 – расходы, связанные с маскировкой одного информационного образа X под образы K1, K2, K3. Тогда определение наилучшего способа маскировки информационных образов X приводит к следующей задаче линейного программирования:
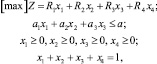 (2)
(2)
где a – ограничение по расходам на маскировку одного информационного образа.
В случае если маскировка сведений X дополнительно требует расходов дефицитных средств в количестве bij единиц j-го материала на один информационный образ при i-м способе маскировки, то необходимо использовать еще условия
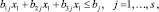 (3)
(3)
где bj – ограничение по j-му фактору.
Результаты
Решим поставленную задачу (2), (3) при следующих значениях постоянных:
C1 = –10; C2 = 10; C3 = 2;
P1(X) = 0,3; P2(X) = 0,2;
P3(X) = 0,4; P4(X) = 0,8;
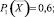
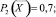
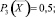
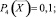
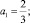
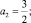
 a = 1;
a = 1;
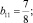
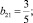
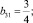 b1 = 1.
b1 = 1.
После вычисления величин Ri по формуле (1) задача линейного программирования запишется в виде
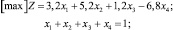
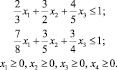 (4)
(4)
Воспользовавшись для решения задачи линейного программирования (4) пакетом анализа Microsoft Excel, получим результаты, изображенные на рисунке.
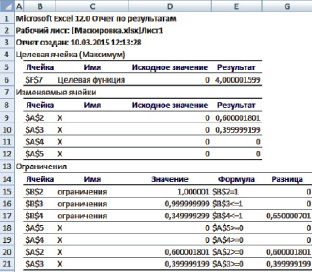
Отчет по результатам решения задачи линейного программирования
Видно, что при заданных величинах выигрышей C1, C2, C3 и ограничениях на расходуемые ресурсы для достижения максимального суммарного выигрыша от маскировки (целевая функция), равного 4, необходимо пользоваться способами маскировки K1, K2 с частостями 60 и 40 % соответственно.
Выводы
Таким образом, в работе показана возможность использования методов линейного программирования для оптимизации маскировки конфиденциальных сведений в открытых источниках информации в условиях конкурентной разведки.
Рецензенты:
Сумин В.И., д.т.н., профессор кафедры управления и информационно-технического обеспечения, ФКОУ ВПО «Воронежский институт Федеральной службы исполнения наказаний», г. Воронеж;
Астахова И.Ф., д.т.н., профессор кафедры математического обеспечения ЭВМ, ФГБОУ ВПО «Воронежский государственный университет», г. Воронеж.
Работа поступила в редакцию 10.04.2015.



