Основой решения задач прогнозирования долговечности работы деталей и конструкций машин, оценки их прочностной надежности является кривая усталости (кривая Велера) [2], связывающая число циклов деформирования (N) с уровнем действующего в опасном месте детали напряжения (σ). Среди математических моделей, используемых для описания кривых усталости, наиболее перспективной является полуэмпирическая модель, разработанная в рамках кинетической теории механической усталости [1, 6], учитывающая процессы накопления усталостных повреждений в материале при циклическом деформировании деталей. В частности, для кривой усталости в малоцикловой области математическая модель имеет следующий вид [1, 6]:
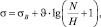(1)
где σВ – предел прочности материала; ϑ – угол наклона кривой усталости в системе координат lgN – σ; N и H соответственно число циклов нагружения и число циклов деформирования до верхней точки перегиба кривой малоцикловой усталости, рассчитываемые по зависимостям
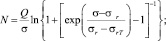
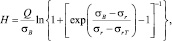(2)
в которых обозначено: Q – коэффициент выносливости; σr – предел выносливости детали при коэффициенте асимметрии цикла r; σrT – циклический предел текучести (ниже его уровня следы пластической деформации даже после нескольких миллионов циклов нагружения отсутствуют).
Алгоритмы и процедуры расчета значений параметров Q, σr, σrT, ϑ модели (1) на основе совокупности данных σi, Ni,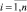 
, полученных в процессе испытаний n образцов на долговечность, рассмотрены в работе [6]. В результате реализации этих алгоритмов определяется кривая усталости в виде регрессионной зависимости N = N(σ), соответствующая 50 % вероятности разрушения (неразрушения) образцов. Естественно, что использовать такую зависимость для прогнозирования долговечности деталей не имеет смысла. В связи с изложенным важнейшим практическим приложением результатов обработки данных усталостных испытаний образцов является не сама кривая усталости, а ее левые (нижние) границы доверительных интервалов, соответствующие, например, вероятности разрушения образцов 1 или 5 %. Цель настоящей статьи состоит в разработке методики расчета точек границ доверительного интервала для кривой малоцикловой усталости в виде (1).
Расчет границ доверительного интервала кривой малоцикловой усталости
Расчет границ доверительного интервала кривой усталости требует знания функции плотности распределения f(N) или f(lgN) при σ = const. Традиционно [2] принимают, что эти функции соответствуют нормальному (логнормальному) закону распределения случайных величин. Однако, как показано в работах [3, 4, 5], функции f(N) и f(lgN) являются существенно более сложными, не описываемыми с помощью законов, исследованных в теории параметрической статистики.
Для решения задачи в настоящей статье реализована идея статистического моделирования, впервые предложенная в работе [4] для получения выборки предела выносливости с целью восстановления его функции плотности распределения методами непараметрической статистики [3, 5].
Из анализа зависимости (1) следует, что она содержит два параметра, природа которых случайная, – это предел прочности (σВ) и число циклов до верхней точки перегиба кривой малоцикловой усталости (H), которое относительно σВ описывается нелинейной зависимостью (2). На момент решения рассматриваемой задачи параметры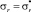 
, 
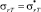, Q = Q*, ϑ = ϑ* известны. Воспользуемся данными разрушения образцов на разрывной машине, на основе которых определим статистические характеристики σВ: среднее значение 
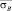и границы его доверительного интервала, например, для вероятности 99 % 
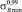и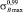 
.
Подставляя в выражение (2)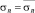 
, 
, 
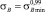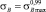, рассчитаем математическое ожидание 
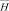числа циклов H, а также границы его 99 % доверительного интервала: 
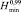и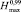 
.
Поставим задачу получения зависимости для кривой усталости, которая проходила через любую экспериментальную точку σi = const, Ni = const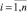 
и находилась в пределах установленных границ доверительного интервала. Введем безразмерную величину χ, используя которую зададим текущие значения σВ и H:
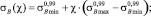
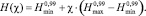(3)
Подставляя функции σВ(χ) и H(χ) в выражение (1), получим
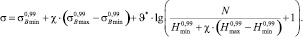(4)
Входя в это выражение при σ = σi = const и N = Ni = const, имеем трансцендентное уравнение относительно одной переменной χ:
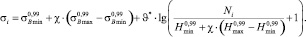(5)
Решая данное уравнение любым численным методом для каждой пары значений σi, Ni,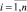 
экспериментальных данных, определим выборку χi, 
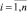, которая позволяет получить серию длиной n кривых малоцикловой усталости:
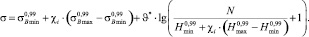(6)
Данная совокупность кривых усталости позволяет сформировать выборку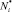 
, 
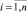при σ = σ* = const:
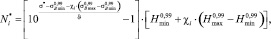(7)
необходимую для решения задачи восстановления неизвестной функции плотности распределения случайной величины N или lgN при σ = σ* = const.
Пусть требуется восстановить функцию плотности распределения числа циклов до разрушения fN(N) при фиксированной величине напряжения σ = σ* = const. Поскольку априори закон распределения случайной величины N неизвестен, воспользуемся математическим аппаратом непараметрической статистики [4], успешно применяемым в последнее время для решения подобных задач [3, 4, 5]. Исходной информацией для определения функции fN(N) является совокупность значений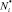 
, 
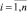, рассчитанная по зависимости (7).
Для восстановления функции fN(N) воспользуемся методом Парзена – Розенблатта [3, 4]. Следуя этому методу, неизвестная функция плотности fN(N) записывается в виде
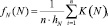(8)
где K(N) – ядерная функция (ядро); hN – параметр «размытости».
На основании работ [3, 4, 5] воспользуемся ядерной функцией с нормальным ядром. В этом случае функция fN(N) описывается выражением
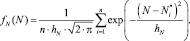(9)
В работе [4] показано, что оптимальное значение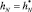 
рассчитывается по формуле
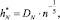(10)
где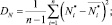 
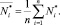
Имея функцию fN(N), требуемая по условиям обработки данных усталостных испытаний при σ = σ* = const величина квантиля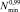 
определяется в результате решения относительно 
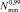численным методом следующего уравнения:
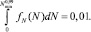(11)
Установленное в процессе реализации изложенного алгоритма значение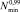 
при заданной величине напряжения σ* = const определяет точку границы доверительного интервала кривой усталости (1), соответствующего вероятности разрушения образцов 1 %. Для расчета других точек этого доверительного интервала достаточно повторить рассмотренную процедуру для напряжений σ* = const в требуемом диапазоне изменения.
Реализация разработанных алгоритмов на примере обработки данных малоцикловых испытаний образцов гибкой трубы HS-80
В работе [6] представлены результаты испытаний на долговечность прямоугольных образцов, вырезанных из гибкой трубы HS-80. Для этих данных осуществим расчет границ доверительных интервалов. На основе обработки данных растяжения образцов на разрывной машине получено
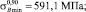
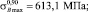
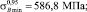
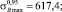
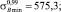
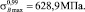
По формулам (2) рассчитаем значения
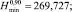
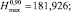
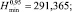
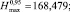
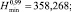
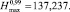
Обратимся к уравнению (5). Решая его численным методом n раз для каждой пары значений σi, Ni, определим выборку безразмерной величины χi,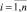 
. После чего для любой фиксированной величины напряжения σ = σ* = const по выражению (7), используя массив χi, 
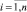, рассчитаем выборку 
, 
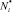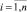. Воспользовавшись математическим аппаратом непараметрической статистики на основе выборки 
, 
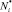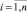, восстановим неизвестную функцию плотности распределения fN(N*), описываемую зависимостью (9). В качестве примера на рис. 1 показана гистограмма распределения 
, 
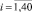и функция fN(N*), – в виде (9), при σ = σ* = 250 МПа. Для расчета границ доверительных интервалов, например при вероятности разрушения образцов 0,5; 2,5; 5 и 50 %, достаточно для ряда фиксированных величин напряжений реализовать рассмотренную процедуру восстановления fN(N*) и рассчитать путем решения интегрального уравнения (11) соответствующие квантильные оценки чисел циклов. Результаты таких выполненных расчетов представлены на рис. 2 в системе координат lgN – σ.
Рис. 1. Функция плотности распределения fN(N*)
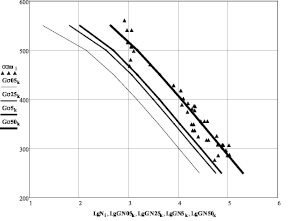
Рис. 2. Границы доверительных интервалов в системе координат lgN – σ
Основные результаты работы
1. Предложен оригинальный алгоритм расчета границ доверительных интервалов для кривой малоцикловой усталости, основанный на использовании математического аппарата непараметрической статистики, позволяющий при решении задачи учитывать фактические законы распределения числа циклов до разрушения при фиксированной величине напряжения.
2. Разработанные методики и вычислительные алгоритмы проиллюстрированы на примере обработки данных малоцикловых усталостных испытаний образцов гибких труб HS-80.
Рецензенты:
Быков И.Ю., д.т.н., профессор кафедры «Машины и оборудование нефтяной и газовой промышленности», ФГОУ ВПО «Ухтинский государственный технический университет», г. Ухта;
Плеханов Ф.И., д.т.н., профессор, директор Глазовского инженерно-экономического института (филиала), ФГОУ ВПО «Ижевский государственный технический университет им. М.Т. Калашникова», г. Глазов.
Работа поступила в редакцию 10.04.2015.