Методы управления, основанные на нечеткой логике, широко распространены на практике уже давно. Однако настройка нечетких регуляторов во многом зависит от экспертных знаний. В настоящее время существуют рекомендации по выбору форм функций принадлежности, по выбору диапазонов изменения входных и выходных величин, по выбору методов фаззификации и дефаззификации [1]. Однако в результате применения всех этих методов нельзя получить оптимальный регулятор. Поэтому конечная его настройка происходит экспертным путем. В данной статье предлагается формализованная методика оптимизации нечеткого регулятора, основанная на применении генетических алгоритмов.

Данная методика предполагает выполнение следующих основных этапов:

1) синтез исходного регулятора;

2) настройка параметров генетического алгоритма;

3) выбор целевой функции;

4) оптимизация регулятора.

Этап 1 предполагает создание исходного нечеткого регулятора. Главное на данном этапе – определить границы входных и выходных переменных, задать формы функций принадлежности, базу правил нечеткого регулятора, а также методы фаззификации и дефаззификации. Подбор оптимальных настроек для термов лингвистических переменных происходит на следующих этапах предлагаемой методики [2].

Этап 2 предполагает настройку параметров генетического алгоритма. То, какие параметры необходимо настроить, сказано ниже.

Этап 3 предполагает выбор целевой функции. Предлагаемая методика позволяет выбирать любую характеристику переходного процесса (или их комбинацию) в качестве целевой функции [4].

Этап 4 включает работу непосредственно генетического алгоритма, который в зависимости от заданных ранее параметров производит оптимизацию регулятора.

Рассмотрим подробнее работу генетического алгоритма. В каждом конкретном случае в качестве целевой функции можно использовать как некоторые числовые показатели переходного процесса, такие как время регулирования или величина перерегулирования, так и интегральные показатели качества – площадь между графиком переходного процесса и единичным графиком, площадь между графиком переходного процесса и желаемым графиком [3].

В качестве варьируемых параметров используются входные и выходные лингвистические переменные нечеткого регулятора. Методика предполагает в процессе работы генетического алгоритма изменение термов лингвистических переменных (рис. 1).

На рис. 1 показаны симметричные формы функций принадлежности, но методика позволяет оптимизировать и несимметричные. В процессе оптимизации происходит варьирование значений a и b для входных и выходных лингвистических переменных. Для этого они зашифровываются в генотипе.

Методика накладывает следующие ограничения на диапазон изменения величин a и b:

1) a – от 0 до верхней границы диапазона;

2) b – от 0 до верхней границы диапазона;

3) b > = a.

Рассмотрим подробнее предлагаемую методику на примере настройки нечеткого регулятора для модели системы, изображенной на рис. 2.

Была разработана программа в среде Matlab, производящая настройку параметров нечеткого регулятора на основе выбранных пользователем характеристик работы генетического алгоритма. На рис. 3 показана экранная форма этой программы.

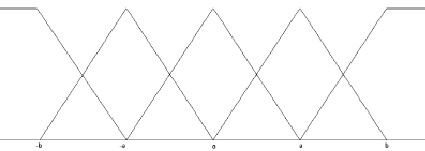
Рис. 1. Варьируемая лингвистическая переменная

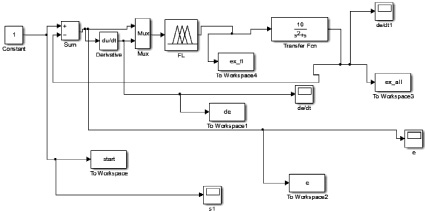
Рис. 2. Модель системы в среде Matlab, на примере которой рассматривается настройка нечеткого регулятора

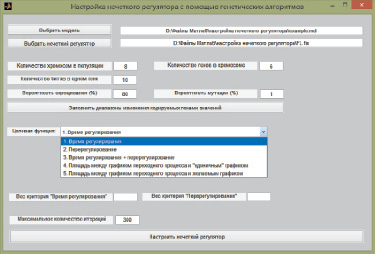
Рис. 3. Экранная форма программы настройки нечеткого регулятора в среде Matlab

Необходимо указать модель, на которой будет производиться настройка регулятора, а также указать исходный нечеткий регулятор. Далее задаются некоторые параметры генетического алгоритма:

1) количество хромосом в популяции;

2) количество генов в хромосоме;

3) количество битов в одном гене;

4) вероятность скрещивания;

5) вероятность мутации;

6) целевая функция.

Ранее было сказано, что методика позволяет использовать в качестве целевой функции любой параметр переходного процесса. Однако в данной версии программы доступны для выбора 5 наиболее популярных вариантов:

а) время регулирования;

б) перерегулирование;

в) время регулирования и перерегулирование одновременно (при этом имеется возможность указать веса обоих критериев);

г) площадь между графиком переходного процесса системы и «единичным» графиком (то есть графиком, у которого каждому значению переменной времени t соответствует выходное значение y = 1);

д) площадь между графиком переходного процесса системы и желаемым графиком (при этом программа позволяет указать желаемую форму переходного процесса аналогично тому, как это сделано в NCD-блоке в программе Matlab);

7) максимальное число итераций естественного отбора.

Оптимизируемый в рассматриваемом примере регулятор содержит две входных (e – ошибка управления, de – скорость изменения ошибки управления) и одну выходную переменную (y). Соответственно, генотип состоит из 6-ти частей: a₁, b₁, a₂, b₂, a₃, b₃. Границы изменения переменных: e – [0; 1,5], de – [0; 2], y – [0; 1,5].

Примем желаемую точность ∆ = 1 %. При этом согласно формуле получим число битов, кодирующих каждый ген n_a1 = n_b1 = n_a2 = n_b2 = n_a3 = n_b3 = 10.

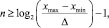(1)

где n – число битов в гене; x_max – верхняя граница изменения кодируемого параметра; x_min – нижняя граница изменения кодируемого параметра; ∆ – требуемая точность.

Для создания начальной популяции возьмем случайные значения варьируемых параметров a и b. В ходе своей работы данная программа преобразует значения этих параметров в генотип, а также выполняет обратную операцию – преобразование генотипа в фенотип – согласно формулам (2) и (3) соответственно.

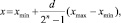(2)

где d – десятичное представление кодируемого параметра; x_max – верхняя граница изменения кодируемого параметра; x_min – нижняя граница изменения кодируемого параметра; n – число битов в гене.

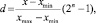(3)

где d – десятичное представление декодируемого параметра; x_max – верхняя граница изменения кодируемого параметра; x_min – нижняя граница изменения кодируемого параметра; n – число битов в гене.

Например, следующие значения параметров: a₁ = 0,6; b₁ = 1,2; a₂ = 0,9; b₂ = 1,8; a₃ = 0,7; b₃ = 1,4 будут зашифрованы в следующей хромосоме:

[[0, 1, 1, 0, 0, 1, 1, 0, 0, 1];

[1, 1, 0, 0, 1, 1, 0, 0, 1, 0];

[0, 1, 1, 1, 0, 0, 1, 1, 0, 0];

[1, 1, 1, 0, 0, 1, 1, 0, 0, 1];

[0, 1, 1, 1, 0, 1, 1, 1, 0, 1];

[1, 1, 1, 0, 1, 1, 1, 0, 1, 1, ]].

По выбору количества хромосом в популяции существуют некоторые рекомендации, но эта тема не рассматривается в рамках данной статьи. Для примера примем число хромосом в популяции равным 8. В качестве целевой функции используем время регулирования переходного процесса системы [5].

а

б

в г

Рис. 4. Параметры входных (а, б) и выходной (в) лингвистических переменных, выходная поверхность (г) исходного нечеткого регулятора

а

б

в г

Рис. 5. Параметры входных (а, б) и выходной (в) лингвистических переменных, выходная поверхность (г) оптимизированного нечеткого регулятора

В качестве метода естественного отбора разработанная программа использует метод «колеса рулетки». Вероятность скрещивания для данного примера установим равную 80 %, вероятность мутации – 1 %.

Параметры исходного нечеткого регулятора представлены на рис. 4.

Параметры нечеткого регулятора, полученного после применения предлагаемой методики оптимизации, представлены на рис. 5.

Результат отработки единичного воздействия, подаваемого на 0-й секунде на вход системы с исходным регулятором, показан на рис. 6, а. Время регулирования переходного процесса в системе с исходным регулятором составило 1,6 с, перерегулирование – 15 %. После оптимизации нечеткого регулятора время регулирования системы составило 0,75 с, перерегулирование составило 3 % (рис. 6, б)

Таким образом, предлагаемая методика позволяет существенно улучшить параметры системы за счет изменения параметров лингвистических переменных нечеткого регулятора. В приведенном примере время регулирования сократилось на 53 %, перерегулирование уменьшилось на 80 %.

а

б

Рис. 6. Переходной процесс системы с исходным нечетким регулятором (а) и с оптимизированным нечетким регулятором (б) при подаче единичного воздействия

Рецензенты:

Гвоздев В.Е., д.т.н., профессор, заведующий кафедрой технической кибернетики, Уфимский государственный авиационный технический университет, г. Уфа;

Куликов Г.Г., д.т.н., профессор, заведующий кафедрой автоматизированных систем управления, Уфимский государственный авиационный технический университет, г. Уфа.

Работа поступила в редакцию 10.04.2015.