Основными видами непреднамеренных помех в метровых (МВ) и декаметровых (ДКМВ) диапазонах волн, используемых для передачи навигационных данных с борта ВС в дифференциальных подсистемах (ДП) при управлении воздушным движением (УВД) с автоматическим зависимым наблюдением (АЗН) и корректирующей информации при дифференциальном режиме работы аппаратуры потребителей спутниковых радионавигационных систем (АП СРНС), являются атмосферные и индустриальные помехи, имеющие квазиимпульсный характер.
Кроме того, для этих диапазонов волн характерно наличие узкополосных помех от мешающих радиотехнических средств.
Задача подавления указанных помех накладывает на приемный тракт РЭО рассматриваемых средств связи противоречивые требования. Так, для подавления квазиимпульсных помех используется ограничитель или «бланкирующее» устройство, запирающее приемник на время действия импульсов помехи.
В то же время нелинейная обработка в условиях узкополосных помех приводит к ухудшению помехоустойчивости РПУ [2].
В условиях негауссовых помех, к которым относятся атмосферные и индустриальные помехи, при малом отношении сигнал/помеха и независимых выборочных значениях смеси оптимальный приемник для выделения сигнала и оценки его параметров состоит из безынерционного нелинейного преобразователя и линейного приемника, оптимального при нормальной помехе [1, 3].
При этом выигрыш Копт в дисперсии оценки параметров сигнала и в отношении сигнал/помеха (по мощности) по сравнению с линейным приемником определяется выражением
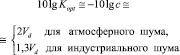, (1)
где с – доля мощности «фоновой» составляющей в общей мощности помехи.
В случае воздействия на РПУ наряду с квазиимпульсной узкополосной помехой нелинейная обработка приводит к обогащению спектра последней, в результате чего при дискретной выборке «пораженными» оказываются частоты fп, имеющие расстройку относительно частоты сигнала f0
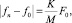(2)
где f0 – частота взятия отсчетов; К и М – целые несократимые числа [6].
Это, в частности, при оценке фазы сигнала приводит к ошибке, максимальное значение которой равно [6]:
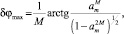(3)
где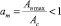 
– отношение максимума огибающей помехи к амплитуде сигнала.
Для подавления узкополосных помех используются режекторные фильтры. Однако при совместном воздействии на РПУ узкополосной и квазиимпульсной помех в результате вырезания части спектра последней появляются осцилляции после окончания импульсов [7] – своего рода узкополосная помеха, снижающая эффективность последующей нелинейной обработки смеси.
Для оценки уровня паразитных продуктов режекции рассмотрим прохождение через режекторный фильтр с селектором в виде одиночного колебательного контура с полосой пропускания (в герцах) a импульсов, формирующих импульсную компоненту квазиимпульсной помехи, дающую основной вклад в ее мощность (для атмосферной помехи – это импульсы от ближних гроз).
Как отмечалось в [7], эти импульсы достаточно хорошо описываются выражением
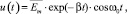(4)
где β – входная полоса (в герцах) РПУ с рабочей частотой ω0;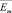 
– среднее значение амплитуд импульсов шума, то есть максимумов его огибающей E(t), распределение которых при равномерном спектре E(t) в рамках логарифмически нормальной модели записывается 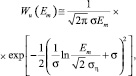[5]
(5)
где ó – параметр модели, связанный с параметром Vd, характеризующим степень импульсности помехи, для атмосферной и индустриальной помех. При этом
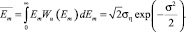(6)
Колебание на выходе режекторного фильтра записывается [5]
Колебание на выходе режекторного фильтра записывается [5]
up(t) = u(t) – Δu(t), (7)
где
Δu(t) = Δu1(t) + Δu2(t) = A exp (–at) ×cos (ω1t – φ) + Β exp (–βt) cos (ω0t – Ψ);
ω1 = (ωn2 – a2)1/2 ≡ ωn;
здесь А, В, φ и ψ – постоянные величины, зависящие от параметров импульса u(t) и фильтра, причем
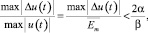(8)
где 
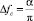и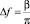 
– соответственно полоса пропускания селектора и ширина спектра u(t), равная входной полосе приемника.
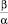раз, обусловлены составляющей Δu1(t) в (7), для которой, очевидно, в качестве верхней границы уровня может быть принято значение, определенное в (8):
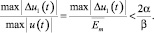(9)
Подстановка (6) в (9) дает
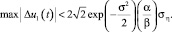(10)
При этом применительно к задаче оценки фазы гармонического сигнала с использованием идеального ограничения смеси имеет место дополнительная ошибка, определяемая выражением (4), где
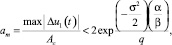(11)
где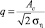 
– отношение сигнал/помеха. При наличии в приемном тракте r режекторных фильтров верхняя граница уровня осцилляций, очевидно, в r раз выше уровня, определяемого выражением (9).
Благодаря частичной компенсации паразитных продуктов режекции Δu(t) узкополосных помех, имеющей место при суммировании колебания с выхода режекторного фильтра и реакции узкополосного фильтра на входные импульсы, их остаточный уровень δu(t) существенно уменьшается по сравнению с Δu(t) и определяется выражением [4]
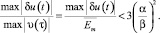(12)
Кроме рассмотренных выше аддитивных помех на РПУ может воздействовать мультипликативная помеха, приводящая к флуктуациям амплитуды и фазы (федингу) сигнала. Интересно проанализировать, сохраняет ли рассмотренная выше обработка смеси сигнала и помехи, являющаяся непараметрической и, как отмечалось, близкой к оптимальной в условиях квазиимпульсных помех, свои непараметрические свойства в условиях наличия флуктуаций амплитуды и фазы сигнала.
Актуальность такого рассмотрения обусловлена тем, что флуктуации амплитуды и фазы сигнала являются довольно распространенным мешающим фактором для приемного РЭО. В частности, федингу подвержены системы дальней радиосвязи ДКМВ диапазона волн, в особенности в высоких широтах в периоды авроральных возмущений ионосферы. Кроме того, в авиационных системах радиосвязи, работающих в МВ диапазоне волн, флуктуации амплитуды и фазы сигнала могут быть вызваны многолучевым распространением сигнала, связанным с отражениями его от элементов рельефа местности и местных предметов.
Рассмотрим плотность вероятностей фазы смеси федингующего сигнала
s(t) =λ(t) A(t) cos {w0t – [ψ(t) + Θ(t)]}, (13)
где λ(t) и Θ(t) – случайные, в общем случае статистически зависимые помехи, модулирующие амплитуду A(t) и фазу ψ(t) сигнала, и аддитивной помехи
п(t) = Е(t) cos [w0t – j(t)] (14)
с равномерным распределением фазы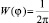
и произвольным распределением огибающей W(E), флуктуации которой, как и в [9], полагаем статистически независимыми от флуктуаций фазы.
При медленном фединге условная совместная плотность вероятностей огибающей и фазы аддитивной смеси сигнала (13) и помехи (14) (при фиксированных параметрах фединга) не зависит от его скорости [7]:
.
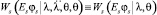При этом условная совместная плотность вероятностей квадратурных компонент смеси: Xs(t) = Es(t) cos φs(t) и Ys(t) = Es(t) sin φs(t) также не зависит от скорости фединга [8]. Ее можно выразить через совместную плотность вероятностей квадратурных компонент аддитивной помехи:
Ws(Xs, Ys |λ, Θ) = W(Xs – x, Ys – y), (15)
где
x(t) = λ(t) A(t) cos [ψ(t) + Θ(t)];
y(t) = λ(t) A(t) sin [ψ(t) + Θ(t)] (16)
– квадратурные компоненты федингующего сигнала.
При слабом сигнале, разлагая W[Xs – x, Ys – y] в ряд по степеням x(t) и y(t) и ограничиваясь тремя членами ряда, из (15) получаем
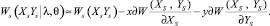(17)
Выражение для совместной плотности вероятностей квадратурных компонент помехи можно выразить через совместную плотность вероятностей огибающей и фазы помехи:
Е(t) = [X2(t) + Y2(t)]1/2,
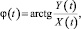
которую, в свою очередь, с учетом принятых допущений о статистической независимости их флуктуаций и равномерности распределения фазы представим в виде:
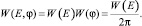(18)
В соответствии с правилами функционального преобразования случайных величин из (18) получим
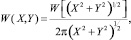(19)
где W(•) – плотность вероятностей огибающей помехи;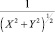 
– якобиан преобразования при переходе от Е,φк X, Y.
Подставляя (19) в (17) и выражая Ws(Еs,φs | λ, Θ) через Ws(Xs, Ys | λ, Θ), с использованием правил функционального преобразования случайных величин и с учетом (16) найдем
(20)
Из (20) для безусловной совместной плотности вероятностей огибающей и фазы смеси запишем
(21)
где W(λ, Θ) – совместная плотность вероятностей параметров фединга l(t) и q(t),
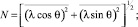(22)
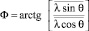, (23)
черта сверху означает усреднение по ансамблю реализаций. При этом для плотности вероятностей фазы смеси, ограничиваясь рассмотрением аддитивных помех с достаточно «гладкой» плотностью вероятностей огибающей W(E) и полагая W(Е)Е = 0 = 0, имеем
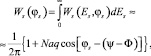(24)
где
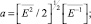
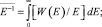
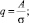
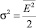– дисперсия аддитивной помехи.
Оценка постоянной на интервале наблюдения фазы сигнала y по критерию максимума правдоподобия, полученная по n независимым выборочным значениям фазы смеси [7], определяется выражением
Ψ* = arctg (Y*/X*), (25)
где
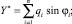
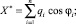
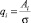– весовые коэффициенты, учитывающие амплитудную модуляцию сигнала.
Решение задачи обнаружения сигнала сводится к получению оценочного значения амплитуды сигнала
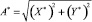(26)
и сравнению его с порогом z.
При высокой точности оценки фазы сигнала, реализуемой при достаточно большом объеме выборки п >> 1, оценочные значения фазы сигнала (25) в первом приближении можно считать распределенными по нормальному закону [9]. При этом смещение и дисперсия оценки определяются выражениями:
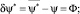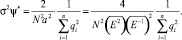(27)
(27′)
Эквивалентное отношение сигнал-помеха, необходимое при решении задачи обнаружения для расчета характеристик обнаружения равно
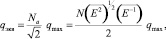(28)
где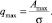 
Существенным обстоятельством является то, что наличие сложной мультипликативной помехи (флуктуаций амплитуды и фазы сигнала) приводит в общем случае к смещению оценки фазы, определяемому выражениями (28) и (23). В частном случае при независимых флуктуациях амплитуды и фазы и симметричных флуктуациях последней и с учетом того, что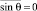 
, из (26) получим
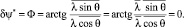(29)
Таким образом, на основании проведенного анализа известное положение об инвариантности к распределению помехи структуры квадратурного приемника с фазовой обработкой входного сигнала, синтезированного в предположении наличия только аддитивной помехи может быть обобщено на случай одновременного действия мультипликативной помехи, которое проявляется в возникновении в общем случае смещения оценки фазы сигнала и в изменении эквивалентного отношения сигнал-помеха на выходе квазиоптимального приемника.
Наряду с рассмотренным выше способом учета изменения характеристик квазиимпульсных помех путем изменения параметров предложенной модели этих помех, позволяющей проводить полунатурные испытания РЭО средств связи, используемых при УВД с АЗН, в близких к реальным условиям эксплуатации, и, соответственно, адекватно оценивать качество функционирования РЭО, возможно использование адаптивных способов обработки сигнала в условиях помех с изменяющимися характеристиками.
Аппроксимация оптимальной характеристики НЭ характеристикой двухстороннего ограничителя с порогом
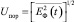(30)
на уровне среднеквадратического значения огибающей фоновой компоненты помехи обеспечивает оптимизацию приемного тракта по отношению к квазиимпульсной помехе.
При этом выигрыш в эффективном отношении сигнал/помеха (по мощности) по сравнению со случаем линейной обработки в соответствии с (2) для случая атмосферной помехи составляет
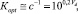(31)
где 
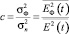(32)
– отношение мощности фоновой составляющей помехи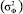 
к общей мощности помехи 
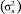; Vd – используемый при описании экспериментальных данных о помехах [7] параметр импульсности, Е(t) и ЕФ(t) – огибающие помехи и ее фоновой составляющей; черта сверху означает усреднение по времени. При оценке параметров помехи по данным измерений в паузе сигнала интервал усреднения Ту должен удовлетворять условию
tк << Ту ≤ tп, (33)
где tк – интервал корреляции флюктуаций помехи во входной полосе РПУ; tп – длительность паузы импульсного сигнала.
Адаптивная обработка смеси сигнала и помехи состоит в автоматическом поддержании оптимального уровня ограничения (30) в условиях изменения помеховой обстановки. Зависимость порогового уровня от параметров помехи, необходимая для построения адаптивного приемника, может быть получена из соотношений (30)–(32). Действительно, из (30) для атмосферной помехи имеем
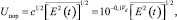(34)
откуда получаем искомую зависимость
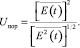(35)
Из (35) видно, что оптимальный пороговый уровень ограничения зависит от интенсивности помехи, характеризуемой величиной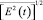 
, и степени ее импульсности, характеризуемой параметром Vd.
Козлов А.И., д.ф.-м., профессор кафедры «Техническая эксплуатация радиоэлектронного оборудования воздушного транспорта», Московский государственный технический университет гражданской авиации, г. Москва;
Акиншин Р.Н., д.т.н., доцент, ведущий научный сотрудник секции по оборонным проблемам Министерства обороны (при Президиуме Российской академии наук), г. Москва.
Работа поступила в редакцию 10.04.2015.