В последнее время сильно возрастает значение исследования систем управления различного вида, различной степени сложности, различных состояний. Методы идентификации нелинейных динамических систем эффективно применяются в задачах восстановления параметров системы и управления сложным техническим объектом в реальном времени. В качестве основной трудности данной задачи можно назвать необходимость быстрой обработки большой базы данных, характеризующей работу идентифицируемой системы с тем, чтобы управление объектом могло осуществляться в реальном времени.
Задача идентификации объектов составляет один из основных этапов создания систем управления и принятия решений. Поскольку реальные объекты обычно характеризуются нелинейной, сложной структурой, а также неполнотой математического описания и информации, как о самом объекте, так и сигналах и помехах, действующих на него, необходимо реализовать задачу идентификации нелинейных систем [5].
Концепция оптимальной линейной фильтрации до недавнего времени имела огромное влияние на развитие различных методов для оценки и обработки стационарных временных последовательностей. Но для современных систем управления характеристика линейного фильтра может быть неприемлема. Типичным примером является случай, когда делается попытка связать два сигнала, чьи основные спектральные компоненты не перекрываются в частотных областях. Поэтому все чаще ставится вопрос применения нелинейных фильтров.
Для решения задачи идентификации нелинейных объектов разработано много подходов и методов [1, 3, 6]. Одним из конструктивных и многосторонних подходов является использование фильтрующей структуры в форме последовательности Вольтерра. Хорошо известны работы Винера по анализу нелинейных систем с использованием белого гауссового входа и так называемых G-функционалов. Метод анализа систем управления на основе рядов Вольтерра был разработан как метод анализа систем уравнений Норбертом Винером, который использовал работу итальянского математика Вито Вольтерра, чтобы получить входные и выходные соотношения для компонентов нелинейных систем уравнений. Винер показал, что так называемый функциональный ряд Вольтерра может быть использован для описания таких систем, пока нелинейность в них не проявлялась слишком сильно.
Следуя его работе, большое число статей были посвящены использованию рядов Вольтерра для оценки и идентификации нелинейных систем [2, 4], однако относительно мало исследователей пытались применить методику фильтрации Вольтерра на практике. Одна из главных причин – это значительная сложность, связанная с разработкой фильтров Вольтерра. Например, многие исследователи используют методику линеаризации, в которой фильтр Вольтерра рассматривается как линейный фильтр с мультиразмерным входным сигналом. Так как особенная структура фильтра Вольтерра не берется во внимание, то возникают серьезные проблемы с матрицами. Количество операций, необходимое для решения проблемы, увеличивается экспоненциально с увеличением порядка фильтра.
В соответствии с этим главное направление в настоящей работе – найти упрощения как в разработке, так и в реализации фильтра Вольтерра (ФВ). Особенно уделим внимание фильтру Вольтерра 2-го порядка, который состоит из параллельной комбинации линейных и квадратичных фильтров, является прототипом нелинейного фильтра, при помощи которого можно улучшить характеристики линейного фильтра, в некоторых случаях значительно, с относительно малой ошибкой вычисления.
Фильтр Вольтерра
Первая проблема, возникающая в разработке нелинейных фильтров, – как точно описать и охарактеризовать их [2]. Опишем фильтр в форме
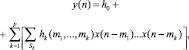(1)
где x(n), y(n) – вход и выход соответственно, а hk (m1, ..., mk) обозначает k-размерные весовые последовательности фильтра с параметром множества Sk.
Множество Sk также указывает область суммирования в m1, ..., mk, которая является ограниченным объектом lk, где k – множество целых чисел.
Так как (1) – это ряд Вольтерра в дискретном времени в p-период, то это фильтр Вольтерра p-го порядка. Для того чтобы избежать ненужных умножений, предположим, что hk (m1, ..., mk) – симметрична, т.е. ее значения не изменяются при любой перестановке элементов m1, ..., mk. Например, h(m1, m2) = h(m2, m1).
Надо отметить один из важных аспектов фильтра Вольтерра – выход фильтра линейный по отношению к весам ФВ. Линейность желательна, когда мы имеем дело с критерием минимальной средней квадратичной ошибки.
Модель системы, идентифицируемой фильтром Вольтерра, представлена на рис. 1. Здесь x(n) и s(n) – это случайные процессы с нулевым математическим ожиданием с дискретным параметром n.
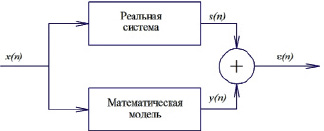
Рис. 1. Структурная схема модели идентифицируемой системы
Фильтр Вольтерра 2-го порядка
Возьмем фильтр Вольтерра 2-го порядка (ФВ2), который состоит из параллельной комбинации линейного и квадратичного фильтров 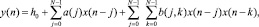[2]:
(2)
где {a(j)} и {b(j, k)} называются линейным и квадратичным весом соответственно, а N указывает длину фильтра (предполагается симметричность квадратичных весов фильтра, т.е. b(j, k) = b(k, j)).
Далее возьмем, что x(n) и s(n) – это случайные процессы с нулевым математическим ожиданием с дискретным параметром n. Нужно найти веса фильтра, которые минимизируют среднюю квадратичную ошибку (СКОШ) между s(n) и выходом фильтра y(n) (предположение нулевого математического ожидания необходимо только для удобства и может быть легко изменено), т.е.
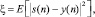(3)
где предполагается строгая стационарность s(n) и x(n) с нулевым математическим ожиданием.
Первым шагом в определении минимума среднеквадратичной ошибки является требование бездрейфового выхода фильтра. Другими словами, должно быть E[y(n)] = 0, так как основной сигнал имеет нулевое математическое ожидание.
Тогда имеем следующее соотношение между h0 и b(j, k):
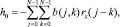(4)
где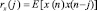 
обозначает автокорреляционную функцию x(n). Важно включение члена нулевого порядка h0. Некоторые из предыдущих исследователей не имели выхода нулевого порядка, но без этого выход минимальной средней квадратичной ошибки фильтра Вольтерра не является обязательно бездрейфовым и ошибка имеет, следовательно, тенденцию к увеличению, в отличие от фильтра Вольтерра 2-го порядка с h0, выраженном в (4).
Подставляя в (2) выражение (4), получим формулу для определения фильтра Вольтера 2-го порядка:
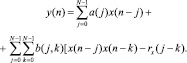(5)
Следующий шаг – определение линейных и квадратичных весов фильтра a(j) и b(j, k), которые определяют минимум среднеквадратичной ошибки.
Выведем простое решение для оптимального фильтра Вольтерра 2-го порядка в предположении, что на входе фильтра гауссиан. Во-первых, заметим, что (5) может быть переписано в виде [7]:
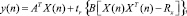(6)
где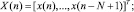 
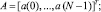
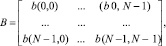
Rx указывает на N×N матрицу от x(n), где rsx(j, k) = rsx(j – k) – автокорреляционная функция входного сигнала x(n). A и B – операторы линейного и квадратичного фильтра соответственно.
Для вывода решения определим кросс-корреляционную rsx(j) и кросс-бикорреляционную tsx(j, k) функции между x(n) и s(n) следующим образом:
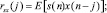
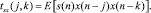
Поскольку предполагается, что s(n) и x(n) – строго стационарны, то как rsx(j), так и tsx(j, k) являются независимыми от переменной n. Кросс-бикорреляционная функция tsx(j, k) определяет статистическую зависимость между s(n) и x(n), которая является критичной при нахождении оптимального квадратичного оператора фильтра. Кроме того, надо сказать, что кросс-бикорреляционная функция является симметричной, т.е. tsx(j, k) = tsx(k, j). Отсюда мы можем получить выражения для определения линейного и квадратичного операторов фильтра.
Программная реализация задачи идентификации нелинейной стационарной системы при помощи фильтра Вольтерра 2-го порядка
Результатом исследования стала программа, которая выполняет ряд действий:
– формирует нормально распределенный входной сигнал x(n);
– формирует нелинейную функцию от входа – выход системы s(n);
– на основе статистической обработки данных вычисляет линейный A и квадратичный B операторы ФВ2, используя корреляционные зависимости сигналов;
– моделирует работу ФВ2, выдавая выход фильтра y(n);
– оценивает остаточную ошибку выхода ФВ2 ε(n);
– оценивает ξ – СКОШ выхода ФВ2;
– строит графики входа/выхода и остаточной ошибки.
Данная программная реализация иллюстрирует асимптотическую сходимость к 0 СКОШ выхода фильтра, отнесенную к дисперсии выходного сигнала. Кроме того, небольшими изменениями в тексте программы можно изменить длину фильтра (в приведенном варианте N = 6), максимальное число обрабатываемых значений сигналов, а также вид нелинейной зависимости.
Примеры работы программы приведены на рис. 2, 3 для значения n = 600.
На рис. 2 изображены графики случайного распределения x(n), а на рис. 3 изображены выход реальной системы, заданный случайными значениями s(n), и выход математической модели в виде фильтра Вольтерра y(n). Программа сама моделирует гауссовый вход x(n) и нелинейный выход системы s(n).
Рис. 2. График случайного распределения x(n)
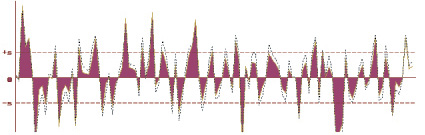
Рис. 3. График выхода реальной системы, заданный случайными значениями s(n), и выхода математической модели в виде фильтра Вольтерра y(n)
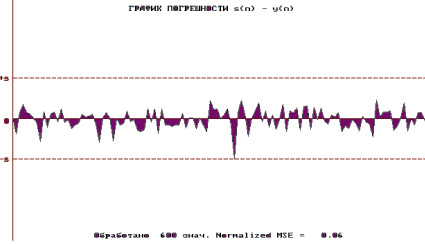
Рис. 4. График ошибки на выходе ε(n)
Следует заметить, что работа ФВ2 происходит в режиме псевдореального времени, т.к. следующие значения сигналов вход/выход вырабатываются (поступают) лишь после того, как будут обработаны предыдущие, т.е. жестко привязаны ко времени работы фильтра.
На рис. 4 показан график ошибки на выходе ε(n) и подсчитана среднеквадратичная ошибка, составляющая в данном случае 6 %, что является очень хорошим результатом для идентификации нелинейных систем. Вообще, для различных значений n от 120 до 1200 среднеквадратичная ошибка колеблется в пределах от 12 до 6 %.
Выводы
Таким образом, задача по определению линейного и квадратичного операторов фильтра Вольтерра 2-го порядка с минимальной средней квадратичной ошибкой для идентификации нелинейных стационарных систем решена и реализована в программном виде. Дальнейшей задачей будет являться усовершенствование этого метода и применение фильтра Вольтерра для идентификации динамических нелинейных систем.
Рецензенты:
Пролетарский А.В., д.т.н., профессор, декан факультета «Информатика и системы управления», зав. кафедрой «Компьютерные системы и сети», МГТУ им. Н.Э. Баумана, г. Москва;
Неусыпин К.А., д.т.н., профессор, профессор кафедры «Системы автоматического управления», МГТУ им. Н.Э. Баумана», г. Москва.
Работа поступила в редакцию 10.04.2015.