Методы математического моделирования, применяемые для исследования процессов питтинговой коррозии [5, 6], позволяют исследовать динамику процесса в области пассивности, а также в областях существования метастабильных и стабильных питтингов.
Моделирование часто основано на результатах электрохимических исследований динамики процессов, среди которых одним из наиболее информативных методов является метод гальваностатической поляризации [4].
В условиях гальваностатической поляризации выделяют три режима локального растворения: автоколебательный, пограничный и режим локально-активного растворения (рис. 1) [3]. В автоколебательном режиме наблюдаются высокочастотные флуктуации потенциала, связанные с зарождением и пассивацией микропиттингов (рис. 1, а). В пограничном режиме наблюдается зарождение и пассивация микропиттингов и макропиттингов (рис. 1, б). Низкочастотные флуктуации потенциала связаны с зарождением, развитием и пассивацией макропиттингов. Наряду с низкочастотными флуктуациями наблюдаются флуктуации потенциала, связанные с пассивацией и повторной активацией поверхности внутри развивающегося питтинга (рис. 1, в).
По хронопотенциограммам, полученным в условиях гальваностатической поляризации, определяют потенциалы активирования и пассивирования поверхности, частоту и амплитуду флуктуаций потенциала. В свою очередь, математические модели, исходными данными которых служат результаты исследования хронопотенциограмм, позволяют получать дополнительные характеристики динамики процессов, такие как индукционное время, вероятность формирования стабильных питтингов на поверхности образца, время появления стабильного питтинга.
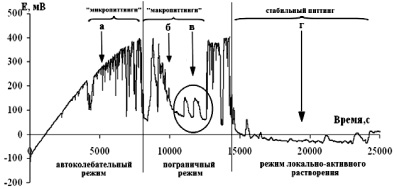
Рис. 1. Хронопотенциограмма стали 12Х18Н10Т в растворе 0,1 М NaCl при плотности поляризующего тока 2,5 мкА/см2
Цель работы заключается в разработке аналитической и имитационной моделей, учитывающих процессы пассивации и повторной активации внутри развивающихся макропиттингов и позволяющих получать дополнительные характеристики локального растворения хромоникелевых сталей в условиях гальваностатической поляризации.
Эксперимент
Для проведения исследований динамики локального растворения в гальваностатических условиях поверхность хромоникелевых сталей марок 08Х22Н6Т, 12Х18Н10Т, 12Х18Н10ТМ образцов (площадь поверхности 1 см2) подготавливали в соответствии с методикой, описанной в ГОСТ 9.912-89 [2].
Поляризационные измерения проводили на потенциостате-гальваностате IPC-Pro в стандартной электрохимической ячейке ЯСЭ-2 при комнатной температуре в условиях естественной аэрации. В качестве электрода сравнения использовали хлорид-серебряный электрод марки ЭВЛ-IМЗ, в качестве вспомогательного электрода – платиновый. В качестве коррозионной среды выбран раствор 0,1 моль/л NaCl.
Гальваностатические условия создавали поляризацией образцов постоянным током, плотность тока подбирали таким образом, чтобы на хронопотенциограммах наблюдались высокочастотные и низкочастотные флуктуации потенциала, свидетельствующие о процессах зарождения, развития и пассивации микро и макропиттингов.
Аналитическое и имитационное моделирование
Процессы возникновения питтингов и пассивации поверхности во времени протекают случайно и могут быть интерпретированы как стохастические, поэтому для моделирования данных процессов применяли теорию цепей Маркова и метод Монте-Карло.
Одним из основополагающих понятий аналитической и имитационной моделей является размеченный граф состояний, который представляет собой схему переходов системы из одного состояния в другое [5].
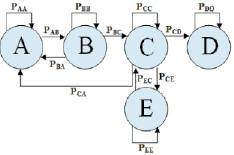
Вершины графа соответствуют различным состояниям поверхности металла: А – пассивное состояние поверхности (питтинги отсутствуют); В – состояние развития «микропиттингов»; С – состояние развитие «макропиттинга»; D – появление стабильного питтинга; Е – «неустойчивая пассивация макропиттинга»; а дуги – условным вероятностям переходов из одного состояния в другое.
Граф состояний также может быть представлен в виде матрицы условных вероятностей перехода, которая является входным параметром аналитической и имитационной моделей.
 а
а 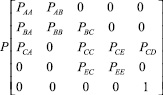 б
б
Рис. 2. а – граф состояний: А – пассивное состояние поверхности (питтинги отсутствуют); В – развитие «микропиттингов»; С – развитие «макропиттинга»; D – появление стабильного питтинга; Е – «неустойчивая пассивация макропиттинга», Pij – условная вероятность перехода из i-состояния в j-состояние; б – матрица условных вероятностей перехода
Матрица условных вероятностей перехода (рис. 2, б) может быть получена на основе обработки хронопотенциограмм, полученных в условиях гальваностатической поляризации.
Аналитическая модель. Аналитическая модель, разработанная на принципах теории цепей Маркова [7], позволяет рассчитать продолжительность процесса локального растворения хромоникелевых сталей до формирования на поверхности стабильного питтинга, в зависимости от начального состояния системы.
Матрицу условных вероятностей перехода (рис. 2, б) представляют в каноническом виде и выделяют квадратную матрицу Q, описывающую переходы между неустойчивыми состояниями A, B, C, E:
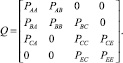 (1)
(1)
Фундаментальная матрица цепи N, которая описывает среднее число попаданий системы в неустойчивое состояние, и матрица N2, характеризующая дисперсию среднего числа попаданий системы в неустойчивое состояние, рассчитываются по уравнениям [7]
N = (J – Q) –1; (2)
N2 = N(2Ndg – J) – Nsq (3)
Если
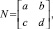
то 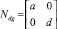 и
и 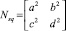 ,
,
где Ndg – диагональная матрица; Nsq – квадрат матрицы; J – единичная квадратная матрица, размерность которой совпадает с размерностью матрицы Q.
Число неустойчивых состояний поглощающей цепи, необходимое для формирования стабильного питтинга, рассчитывается согласно выражению
H = N∙ξ, (4)
где ξ – вектор, составленный из единиц, имеющих соответствующую размерность.
Задав среднюю продолжительность интервала между шагами, получают матрицу H, которая характеризует время требующееся системе для попадания в поглощающее состояние.
Имитационная модель. В основу имитационной модели заложен метод Монте-Карло [1]. Для каждого состояния в табличном виде задается закон распределения, описывающий значения вероятностей (Sn) нахождения системы на следующем шаге в одном из состояний. Алгоритм работы имитационной модели состоит из следующих шагов:
1. Если на начальном этапе поверхность металла находится в состоянии Si, закон распределения данной случайной величины, описывающей переход системы в другое состояние, имеет вид
|
Si |
S1 |
S2 |
… |
Sn-1 |
Sn |
|
Pij |
Pi1 |
Pi2 |
… |
Pi(n-1) |
Pin |
Заданные вероятности пяти состояний образуют полную группу, т.е.
Pi1 + Pi2 + … + Pi(n-1) + Pin = 1.
2. Разбиваем интервал (0,1) на n частичных интервалов Δn:
Δ1 – (0; Pi1), Δ2 – (Pi1; Pi1 + Pi2), …, Δn-1 – (Pi1 + Pi2 + … + Pi(n-2); Pi1 + Pi2 + … + Pi(n-2) + Pi(n-1)), Δn – (Pi1 + Pi2 + … + Pi(n-2) + Pi(n-1); 1)
3. Датчик случайных чисел генерирует число r в интервале от (0, 1). В зависимости от того, в какой из частичных интервалов попала случайная величина r, определяется следующее состояние системы.
4. Действия 1–3 повторяются до попадания системы в состояние Sn (развитие стабильного питтинга), которое является поглощающим.
5. Время до попадания системы в поглощающее состояние можно рассчитать как произведение числа шагов на продолжительность одного шага.
На основании имеющейся последовательности состояний и принятых функциональных зависимостей, описывающих изменение потенциала в каждом из состояний, можно моделировать изменение потенциала системы в ходе коррозионного процесса.
6. Когда система находится в пассивном состоянии («A»), происходит нарастание потенциала, связанное с процессом заряжения емкости двойного слоя, которое предложено описывать выражением вида: E = kτn, где n – показатель степени, больший нуля; τ – текущее время.
7. При развитии «микропиттингов», вследствие уменьшения плотности тока в питтинге, значение потенциала уменьшается, в первом приближении принято, что
E = Ei–1 – k1t1.
8. При развитии «макропиттингов» принят показательный закон изменения потенциала
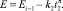
9. В состоянии «неустойчивая пассивация макропиттинга» нарастание потенциала предложено описывать выражением вида
E = Ei–1 + k3t3.
Для получения дополнительных характеристик питтингостойкости, в качестве которых выступают входные и выходные параметры моделей, был разработан комплекс программ, реализующий алгоритмы, заложенные в основу моделей, и алгоритмы расчета входных параметров модели по экспериментальным данным.
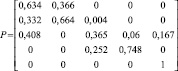
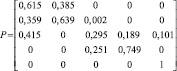
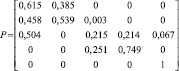
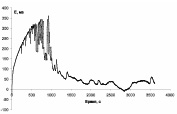
Для трех исследуемых марок стали, на основе анализа флуктуаций потенциала на хронопотенциограммах (рис. 3), получены матрицы условных вероятностей перехода (таблица), которые были взяты в качестве исходных значений входных параметров аналитической и имитационной модели.
Время появления стабильного питтинга на поверхности сталей 08Х22Н6Т, 12Х18Н10Т, 12Х18Н10ТМ, рассчитанное по аналитической и имитационной моделям, а также фактическое значение приведены в таблице.
Сопоставление значений матриц условных вероятностей перехода по вероятностям перехода в состояние развития стабильного питтинга позволяет расположить стали в порядке увеличения их значений:
12Х18Н10ТМ < 12Х18Н10Т < 08Х22Н6Т.
При сравнении результатов расчетов времени до формирования стабильного питтинга по аналитической и имитационной модели установлено, что количество переходов из одного неустойчивого состояния в другое при аналитическом моделировании превышает количество переходов (Н), рассчитанное на основании имитационного моделирования.
 а
а 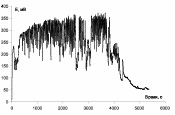 б
б 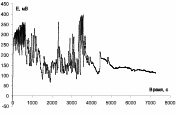 в
в
Рис. 3. Хронопотенциограммы сталей в растворе 0,1 моль/л NaCl, при плотности тока 3 мкА/см2: а – 08Х22Н6Т; б – 12Х18Н10Т; в – 12Х18Н10ТМ
Результаты аналитического и имитационного моделирования
|
Марка стали |
Матрица условных вероятностей перехода |
Время до формирования стабильного питтинга, с |
||
|
Аналитическое моделирование |
Имитационное моделирование |
Фактическое время |
||
|
08Х22Н6Т |
|
1658 |
806 |
1410 |
|
12Х18Н10Т |
|
4957 |
3475 |
4457 |
|
12Х18Н10ТМ |
|
6270 |
4345 |
4841 |
Коэффициент достоверности аппроксимации R2, рассчитанный по формуле
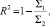
где 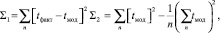 n = 3
n = 3
для имитационной модели равен 67 %, а для аналитической модели –70 %. В то время как усреднение результатов аналитического и имитационного моделирования увеличивает коэффициент достоверности аппроксимации до 87 %.
Таким образом, матрица условных вероятностей перехода, время до появления стабильного питтинга, рассчитанное по аналитической и имитационной моделям, могут быть использованы в качестве дополнительных характеристик питтингостойкости хромникелевых сталей.
Выводы
1. Предложены аналитическая и имитационная модели локального растворения, которые позволяют более полно описывать динамику процесса локального растворения хромоникелевых сталей в условиях гальваностатической поляризации и учитывать процессы повторной активации и пассивации поверхности, протекающие на фоне развития макропиттинга.
2. Разработан комплекс программ для реализации алгоритмов, заложенных в основу аналитической и имитационной моделей, и расчета их параметров.
3. Показано, что входные и выходные параметры аналитической и имитационной моделей могут быть использованы в качестве дополнительных характеристик динамики локального растворения хромоникелевых сталей.
Рецензенты:
Сысоев В.А., д.т.н., декан факультета наноматериалов и нанотехнологий, профессор кафедры плазмохимических и нанотехнологий высокомолекулярных материалов, ФГБОУ ВПО «КНИТУ», г. Казань;
Шаехов М.Ф., д.т.н., профессор кафедры плазмохимических и нанотехнологий высокомолекулярных материалов, ФГБОУ ВПО «КНИТУ», г. Казань.
Работа поступила в редакцию 10.04.2015.