Довольно быстро после открытия ядерного магнитного резонанса (ЯМР) названное явление составило основу мощного метода исследования строения вещества и его свойств, по крайней мере, в жидкой фазе. Основными объектами исследований методами ЯМР молекулярного строения длительное время оставались, главным образом, диамагнитные соединения. Несмотря на то что такая ситуация сохраняется и до сих пор, теперь есть все основания утверждать, что изучение явления ЯМР в парамагнитных системах также позволяет получать ценную информацию о молекулярном строении. Такая возможность относится, как правило, к парамагнитным комплексам, специфика которых определяется неспаренными электронами на d- и f-орбиталях. Электронно-ядерное или сверхтонкое взаимодействие (СТВ) между неспаренными электронами и ядрами парамагнитной молекулы приводят к характерным сдвигам и уширениям, связанным явной функциональной зависимостью с пространственной и электронной структурой молекулы, спектр ЯМР которой детектируется. Для парамагнитных веществ возможны разнообразные по природе релаксационные эффекты, что существенно расширяет возможности ЯМР как метода исследования. Изучение температурной зависимости парамагнитных сдвигов и уширений сигналов позволяет находить термодинамические параметры процесса комплексообразования в растворе, изучать стехиометрию комплексов, а также особенности внутри- и межмолекулярных обменных процессов. Отсюда следует, что спектры ЯМР, трансформированные СТВ, позволяют, по крайней мере, в принципе получать обширную, зачастую уникальную информацию о строении молекул [1–11].
Успех использования указанных выше особенностей ЯМР в парамагнитных системах во многом обусловлен тем, насколько глубоко изучен механизм СТВ и процессы релаксации в молекулярной системе, спектр ЯМР которой анализируется. Принципиальным является также тот факт, что успешное детектирование спектров ЯМР во многом определяется природой процессов релаксации, характерных для изучаемой парамагнитной молекулярной системы. Данные процессы в сильной степени зависят от времени релаксации (τe) неспаренных электронов в таких системах. В свою очередь величина τe зависит от природы парамагнитного центра и может меняться в широких пределах в ряду как d-, так и f-элементов. Так в парамагнитных молекулярных системах, в которых центральным ионом является ион кобальта Co2+, величина τe по порядку величины равна 10-12 с, в то время как для аналогичных систем, образованных ионами Cu2+ и Mn2+, она может увеличиваться до величины порядка ~ 10-8 с.
Неудивительно поэтому, что детектирование спектров ЯМР, трансформированных сверхтонким взаимодействием, требует определенных, часто существенных усилий и отдельно разработанной методики в сравнении со спектрами от диамагнитных соединений. Более того, очень часто парамагнитные уширения делают такую возможность вообще проблематичной задачей. Особенно это относится к сигналам ЯМР от атомов углерода, азота, других атомов, которые составляют остов молекулы. Действительно, уширение сигналов от протонов могут достигать сотни и даже тысячи герц. Что касается углеродных сигналов, то они могут уширяться настолько сильно, что получение спектров ЯМР становится невозможным. В немалой степени поэтому работы, авторы которых используют указанные особенности для решения различного рода физико-химических задач, во всем научном мире все еще остаются немногочисленными.
В данной работе рассматривается ряд аспектов, понимание которых может способствовать расширению круга соединений, доступных для их изучения методами ЯМР. Этому предпослано краткое рассмотрение общих положений ЯМР парамагнитных молекул с ориентацией на обзор [1] и монографию [2], в которых можно найти ссылки как на обзорные, так и на оригинальные публикации других авторов, изучавших обозначенные здесь проблемы.
Релаксационные эффекты в спектрах ЯМР парамагнитных молекул
Парамагнитные ионы могут вызывать значительное уменьшение времен релаксации T1 и T2 ядерных спинов за счет сильных флуктуирующих магнитных полей, генерируемых неспаренными электронами, магнитный момент которых на три порядка превосходит максимальные ядерные магнитные моменты.Обычно используются так называемые модифицированные уравнения Соломона – Бломбергена). Исходным моментом теории Соломона – Бломбергена явилось представление о взаимодействии между неспаренными электронами, центрированными на координирующем ионе, и резонирующими ядрами лигандов в приближении точечного диполя. Это означает, что имеет место следующее соотношение:
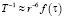, (1)
где T – времена релаксации ядра (продольное T1 или поперечное T2); r – расстояние от него до координирующего иона; f(τ) – функция, явный вид которой определяется, в частности, соотношением между временами корреляции, характеризующими электронно-ядерное взаимодействие (контактное и псевдоконтактное) в системе. Поэтому проблемой исследования релаксационного процесса в парамагнитных комплексах, в первую очередь, оказывается установление явного вида функции f(τ) в выражении (1).
Широко распространенным случаем в практике как фундаментальных, так и прикладных исследований является исследование парамагнитных комплексов в жидкой фазе. В общем случае необходимо принимать во внимание процесс обмена молекул лиганда между первой координационной сферой центрального иона и раствором. Если в образце существует один комплекс определенного состава, выражения Соломона – Бломбергена могут быть представлены в следующем виде:
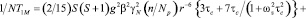
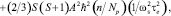(2)
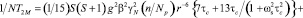
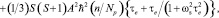(3)
где T1M и T2M – время продольной и поперечной релаксации резонирующего ядра в комплексе; n – число ядер в парамагнитном комплексе; Np – молярная концентрация резонирующих ядер; N – молярная концентрация парамагнитных ионов; A – константа контактного СТВ, определяемая формулой Ферми; ωs – частота ларморовой прецессии электронов; τe и τc – времена корреляции контактного и псевдоконтактного взаимодействия соответственно (остальные обозначения имеют общепринятые значения):
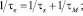
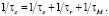(4)
Здесь τs – время релаксации электронного спина, τr – время переориентации парамагнитной частицы, τМ – время жизни молекулы лиганда в первой координационной сфере комплекса. Поскольку τe и τc являются характеристиками случайных процессов, то для каждой конкретной ситуации необходимо специальное рассмотрение. Еще одно очевидное замечание – зависимость времен релаксации T1M и T2M от значения резонансной частоты для конкретного резонирующего ядра.
Здесь уместно следующее отступление. Стремительный рост синтезируемых и выделяемых из природного сырья соединений существенно расширил круг соединений, доступных для изучения в них СТВ. Этому способствует и распространение фурье-спектрометров ЯМР с резонансной частотой по протонам в 400 МГц, 500 МГц и выше с широкими возможностями манипулирования детектируемой спектральной информацией. В свою очередь встает задача более глубокого теоретического осмысления релаксационных процессов в парамагнитных системах. Такая необходимость в определенной степени подтверждают результаты исследования явления ЯМР в сложных, стерически нежестких парамагнитных системах, содержащих в качестве окружения центрального металла многоэлектронные гетероатомные структуры.
Очень часто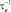 
и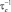 
могут заметно отличаться от ωs, предопределяя вклады псевдоконтактного и контактного взаимодействия в T1M и T2M. Например, если принять во внимание типичные значения τs ≈ 10–8 с (Mn2+ , Cu2+ ), τM ≈ 10–3 с, τr ≈ 10–12 с, при частоте (v) резонанса по протонам в несколько десятком МГц уже выполняются неравенства:
ωs·τe >> 1, ωs·τc << 1. (5)
При выполнении неравенств (5) выражения (2) и (3) могут заменяться другими:
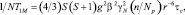(6)
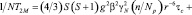
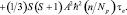(7)
При указанных выше значениях τs, τr, τM повышение частоты резонанса усиливает соотношение ωs·τe >> 1 и ослабляет условие ωs·τc << 1. Тем не менее для частот, характерных для современных спектрометров, оно остается справедливым. Ясно, что помимо частоты ωs, выполнение неравенств (5) зависит от τe и τc, характеризующих природу СТВ парамагнитной молекулы. Например, если принять, что τs ≈ 10–12 с (Co2+ ), τM ≈ 10–3 с, τr ≈ 10–12 с, нетрудно видеть, что даже при частоте резонанса по протонам в несколько сот мегагерц ωs·τe << 1. Таким образом, неравенства (5) принимают вид:
ωs·τe << 1, ωs·τc >> 1. (8)
В этом случае
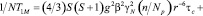
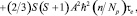(9)
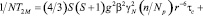
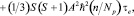(10)
т.е. 1/T1M = 1/T2M . (11)
Обращает внимание тот факт, что последнее выражение для 1/T2M , как и предыдущее, содержит второе слагаемое, которое определяет величину контактного вклада. Однако он существенно меньше, так как τe в (6) много меньше τe в (5).Еще с семидесятых годов прошлого века типичным стало значение v = 100 МГц, затем 200 МГц, а теперь 400 и выше МГц. Ясно, что технические параметры спектрометра ЯМР следует принимать во внимание как при детектировании сигналов ЯМР от парамагнитных частиц, так и при сопоставлении их, снятых в различных условиях. Тем более, что времена релаксации T1M и T2M , а значит и ширины сигналов резонирующих ядер, входящих в состав парамагнитной молекулы, существенно нелинейным образом зависят от входящих в правые части формул (2) и (3) переменных.
Значение A, которое может быть как положительным, так и отрицательным, определяется магнитным моментом неспаренных электронов парамагнитной частицы и ориентацией неспаренного электрона на данном ядре. Согласно формуле Ферми
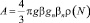, (12)
где gn – ядерный g – фактор; βn – ядерный магнетон; ρ(N) – плотность неспаренного электронного спина на резонирующем ядре. Имеются в виду неспаренные электронные спины, делаколизованные на соответствующие s-орбитали атомов, в состав которых входят резонирующие ядра. Если остановиться на качественном рассмотрении явления ЯМР в парамагнитных системах, то можно воспользоваться часто используемыми представлениями о передаче возмущающегося воздействия неспаренных электронов на резонирующие ядра лигандов как по химическим связям (спиновая деклокализация), так и по механизму спиновой поляризации. Именно в случае спиновой делокализации неспаренные электроны попадают в σ-систему, а значит и на s-орбитали. Отсюда можно сделать вывод о том, что в тех парамагнитных системах, в которых нет прямой делокализации нескомпенсированной электронной спиновой плотности на s-орбитали молекул лигандов, должно наблюдаться дальнейшее уменьшение контактного вклада во времена релаксации T1M и T2M, задаваемые выражениями (7) и (8). Следовательно, в спектрах ЯМР таких систем можно ожидать, что резонансные сигналы будут достаточно узкими и доступными для детектирования.
Заключение
В данной публикации проведен анализ особенностей релаксации ядерных спинов в парамагнитных системах с учетом обменных процессов. В основу анализа положены модифицированные уравнения Соломона – Бломбергена. В этой связи обсуждаются условия детектирования сигналов ЯМР образцов, содержащих растворы парамагнитных структур, в зависимости от резонансной частоты спектрометра ЯМР, а также характеристических времен релаксации.
Рецензенты:
Власов В.Г., д.ф.-м.н., профессор, заведующий кафедрой математики Иркутского государственного технического университета Министерства образования и науки РФ, г. Иркутск;
Барышок В.П., д.х.н., профессор, профессор кафедры химической технологии Иркутского государственного технического университета Министерства образования и науки РФ, г. Иркутск.
Работа поступила в редакцию 01.04.2015.