Определение эффективности тепло- и массообменных контактных устройств в химической технологии часто выполняется c использованием модели структуры потоков: диффузионной и ячеечной. В диффузионной модели основным параметром идентификации является коэффициент обратного (продольного) перемешивания. Этот коэффициент находится экспериментально для каждого типа контактного устройства (аппарата) [2, 3, 7, 9].
Целью данной работы является приближенное определение коэффициентов турбулентного перемешивания в аппаратах различных конструкций без специальных внутренних устройств (перегородок, решеток, клапанов и т.д.)
Известен подход, когда все гидродинамические эффекты – турбулентная диффузия, продольное и поперечное перемешивание в потоке могут быть приближенно описаны с использованием эффективного коэффициента
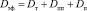, (1)
где Dт – коэффициент турбулентной диффузии, м2/с; Dпп, Dп – коэффициенты продольного и поперечного перемешивания, м2/с. Молекулярная диффузия не учитывается, т.к. для ядра потока ее роль в переносе очень мала.
С коэффициентом перемешивания Dэф в одномерном приближении записывается диффузионная модель структуры потока
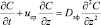, (2)
где С – концентрация компонента; t – время, с; uср – средняя скорость среды в направлении z; z – продольная координата, м.
Таким образом, введение Dэф позволяет в интегральном виде приближенно учитывать все неоднородности в аппарате.
Для однофазного потока в цилиндрическом канале Тейлор получил
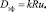, (3)
где R – радиус канала, м; u* – динамическая скорость, м/с (скорость касательного напряжения); k = 10,1. Рассмотрим далее применение выражения (3) для различных условий движения одно- и двухфазных сред.
Однофазный поток в канале
Первоначально рассмотрим применение выражения (3) для канала с однофазной средой при турбулентном режиме.
Используя выражения для динамической скорости в трубе, запишем
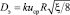. (4)
Отсюда число Пекле
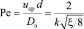, (5)
где d – диаметр канала, м; uср – средняя скорость среды м/с; ξ – коэффициент сопротивления.
Для сравнения используем выражение Дильмана В.В. по перемешиванию в газовой фазе неорошаемого канала
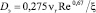(6)
или
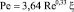, (7)
где Rе = uсрd/v – число Рейнольдса; v – коэффициент кинематической вязкости м2/с.
Например, при Rе = 104 по формуле (7) (ξ = 0,316Rе–0,25) имеем Ре = 2,48. При Rе = 105, Ре = 2,99. Аналогичные значения (± 10 %) получаем по формуле (5) при k = 13,2, что несколько больше значений Тейлора.
С коэффициентом сопротивления по Блазиусу из (5) и (7) получаем, соответственно
, 
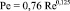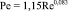. (8)
При Rе = 5·103 до 5·105 расхождение значений Ре по формулам (8) составляет не более 12 %, что говорит о справедливости подхода Тейлора.
Орошаемые каналы
Вероятно, что формулу (5) можно использовать для шероховатых каналов и каналов с орошаемых поверхностью (стекающей пленкой) с соответствующими коэффициентами ξ. Характер зависимости (5) показывает, что при увеличении гидравлического сопротивления (коэффициента ξ) число Ре уменьшается, что говорит о повышении интенсивности перемешивания – т.е. коэффициента Dэф.
Например, для канала с полным проявлением шероховатости (автомодельный режим) ξ ≈ 0,08 и число Ре = 1,52, а для гладкого канала Ре = 2,41 (Re = 104).
Для круглого канала с орошаемой стенкой получено [7]
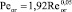, (9)
где Реог uср (d – 2δпл)/Dэф; Reог = uср (d – 2δпл)/vг; δпл – толщина пленки, м.
Из выражения (5) с k = 13,2 запишем
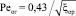, (10)
где ξор = f (Reог) – коэффициент сопротивления орошаемого канала.
Например, при Rе = 5·103, ξор = 0,055; при Rе = 5·104, ξор = 0,05 (экспериментальные данные (рис. 3–1 [7]), (Reж = 50 – 400). По формуле (10) получаем при Rе = 5·103, Реог = 1,83; при Rе = 104, Реог = 1,92. По формуле (9) соответственно получаем: Реог = 2,93 и Реог = 3,04. Как видим, расхождение ~ 50 % и формула (9) дает завышенное значение числа Пекле, по сравнению с формулой Тейлора (10). Такой же вывод сделан и в работе [7]. Однако формула (9) не проверена по экспериментальным данным для орошаемых трубок. Кроме этого, результаты расчетов по формуле (10) зависят от достоверности определения коэффициента ξор.
Сравним с формулой Борисова [9]
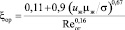, (11)
где uж – скорость жидкости в пленке, м/с; μж – вязкость жидкости, Па, с; σ – поверхностное натяжение, Н/м.
При Reж = 100, толщина пленки: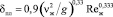 
и δпл = 2·10–4, м; Reж = 4q/vж; Приведенный расход: q = 2,5·10–5 м3/(м·с); uж = q/δпл = 0,125 м/с. Коэффициент (11) ξор = 0,031 при Rеог = 5·103; и ξор = 0,028, при Rе = 104. С полученными значениями ξор по формуле (10) имеем при Rе = 5·103, Реог = 2,44; при Rе = 104, Реог = 2,56.
Расхождение с формулой (9) стало меньше и составляет около 20 %, что вполне приемлемо для двухфазных сред. При числе Рейнольдса пленки Reж = 400 число Пекле (10) снижается на 5 %, т.е. коэффициент эффективного перемешивания увеличивается, но незначительно.
Для орошаемого канала прямоугольного сечения получено [7]
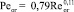. (12)
Коэффициент сопротивления плоскопараллельного орошаемого канала
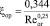. (13)
Из формулы (10) с коэффициентом (13) получим
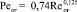. (14)
Даже без расчетов следует хорошее согласование выражений (12) и (14).
Таким образом, показана принципиальная возможность использования формулы (10) для орошаемых круглых и плоскопараллельных каналов при противоточном турбулентном движении газа. Полученные результаты имеют практическое применение при расчетах регулярных насадочных контактных устройств с использованием диффузионной модели (2).
Однофазный поток в хаотичной насадке
Рассмотрим турбулентное движение (Reэ > 50) однофазного потока в хаотичном насадочном или зернистом слое. Представляя насадочный слой в виде совокупности эквивалентных каналов, запишем коэффициент перемешивания с использованием формулы (3)
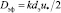, (15)
где Reэ = uсрdэ/v – число Рейнольдса; dэ – диаметр эквивалентной насадки, м; u* – средняя динамическая скорость на поверхности элементов [5]
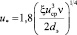, (16)
где ξ – коэффициент гидравлического сопротивления насадки, ξ = f(Reэ) [5, 9].
После идентификации с экспериментом [8] из выражения (15) с u* (16) получено
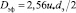(17)
или
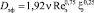. (18)
Отсюда число Пекле [6]
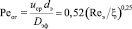. (19)
Сравнение с экспериментальными данными [8] показано на рис. 1.
Пленочный режим в насадке
Можно предположить, что формулу (18) и полученную на ее основе (19), записанную в виде
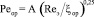, (20)
можно использовать для приближенных расчетов и для газовой фазы при пленочном течении жидкости в противотоке по поверхности насадочных элементов, при соответствующем определении коэффициента ξор орошаемой насадки и корректировании по опытным данным коэффициента пропорциональности А. При неизвестном значении А в первом приближении можно принять А = 0,52.
Коэффициент сопротивления орошаемой насадки при пленочном режиме находят из модифицированного выражения Дарси-Вейсбаха [9]
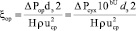, (21)
где ΔPop, ΔPcух, – перепады давлений для сухой и орошаемой насадки, Па; H – высота слоя насадки, м; b-эмпирический коэффициент; U – плотность орошения, м/ч (м3/(м2 ч)).
Например, коэффициенты для колец Рашига 25 мм внавал: b = 51·10–3; 50 мм: b = 47·10–3. Колец Палля 50 мм: b = 35·10–3.
Из выражения (21) следует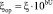 
.
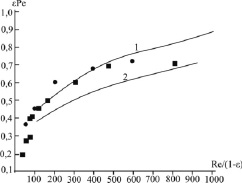
Рис. 1. Зависимость модифицированного числа Pe от числа Re: 1 – расчет по выражению (19) для седлообразных насадок Берля ; 2 – расчет по выражению (19) для колец Рашига; ● – экспериментальные данные Вермюлена для седлообразных насадок Берля; ■ – экспериментальные данные Вермюлена для колец Рашига
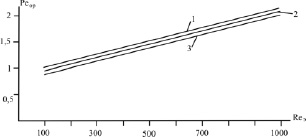
Рис. 2. Зависимость числа Пекле орошаемой насадки в газовой фазе от числа Рейнольдса. 1 – сухая насадка; 2 – U = 20 м/ч; 3 – U = 50 м/ч, dэ = 0,017, м
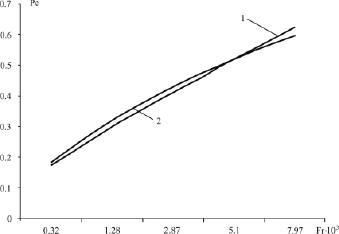
Рис. 3. Сравнение результатов расчетов числа Pe от числа Фруда при wг = 0,05–0,25 м/с и Dк = 0,8 м: 1 – по формуле (24); 2 – по эмпирическому выражению Kato Y., Nishiwaki A.
На рис. 2 в качестве примера показаны результаты расчетов числа Реор (20) для колец Рашига при различных плотностях орошения (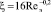
).
Из рис. 2 следует, что при повышении плотности орошения перемешивание увеличивается, но не очень значительно. Для регулярных насадок при идентичных режимных параметрах и эквивалентном диаметре насадки число Пекле получается в три и более раз выше, чем для хаотичных, что указывает на значительное снижение перемешивания в регулярных структурах.
Барботажные аппараты
Рассмотрим применения выражения (3) для расчета барботажных аппаратов с высоким слоем жидкости.
С точки зрения продольного перемешивания, т.е. по высоте слоя в ядре жидкой фазы, пустотелые барботажные колонны близки к аппаратам идеального смешения. Но при малых скоростях газа основную роль в продольном перемешивании играют турбулентные пульсации, обусловленные деформацией газовых пузырей и турбулентностью в следах за пузырями [1, 10].
В выражении (3) предполагается, что перемешивание в основном вызвано за счет турбулентных пульсаций и Dэф зависит от масштаба аппарата в первой степени, что не всегда соответствует действительности.
Выражение для расчета динамической скорости в жидкой фазе получено в виде [10]
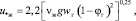(22)
где φг – среднее объемное газосодержание; wг – скорость газа на полное сечение аппарата, м/с; vж – коэффициент кинематической вязкости жидкой фазы, м2/с.
Газосодержание вычисляется по известным эмпирическим выражениям.
Из (3) и (22) запишем число Пекле для перемешивания
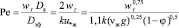, (23)
где Dк – диаметр колонны, м.
После идентификации с экспериментальными данными [10] с учетом масштабного перехода получено [4]
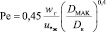, (24)
DМАК = 0,1 м – диаметр макета аппарата, м (0,1 ≤ Dк ≤ 1,0 м).
На рис. 3 приведены сравнения результатов расчета по формуле (24) с расчетом по эмпирическому выражению [9]. Установлено удовлетворительное согласование.
Как следует из представленных результатов [4], выражение (24) дает удовлетворительное согласование с экспериментальными данными различных авторов, обобщенных в работах [9, 10].
Выводы
При проектировании или модернизации аппаратов химической технологии важное значение имеет достоверный расчет профиля концентраций компонентов. Для таких расчетов широко используются диффузионная модель и численные методы. В статье показана возможность определения основного параметра данной модели: коэффициента эффективного перемешивания с помощью уравнения Тейлора. Проведен ряд примеров для контактных устройств различных конструкций и сравнение по коэффициентам перемешивания с известными экспериментальными данными и эмпирическими выражениями. Данной подход позволяет сократить число экспериментальных исследований при разработке новых конструкций аппаратов.
Статья выполнена в рамках проектной части государственного задания в сфере научной деятельности. Задание № 13.405.2014/К.
Рецензенты:
Мингалеева Г.Р., д.т.н., заведующая лабораторией моделирования систем производства энергии Казанского научного центра РАН, г. Казань;
Мутрисков А.Я., д.т.н., профессор кафедры «Энергообеспечение предприятий и энергоресурсосберегающих технологий», ФГБОУ ВПО «Казанский государственный энергетический университет», г. Казань.
Работа поступила в редакцию 01.04.2015.